2020-2021学年八年级数学人教版下册18.2.2.2菱形的判定课件(共39张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.2.2.2菱形的判定课件(共39张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
18.2.2.2
菱形的判定
学习目标
1
2
3
掌握菱形的三种判定方法
渗透类比思想,体会研究图形判定的一般思路
在探究和应用的过程中提高几何直观能力和推理能力
学习重难点
重点
难点
菱形的判定及应用
菱形的判定的探索及解题思路的体会
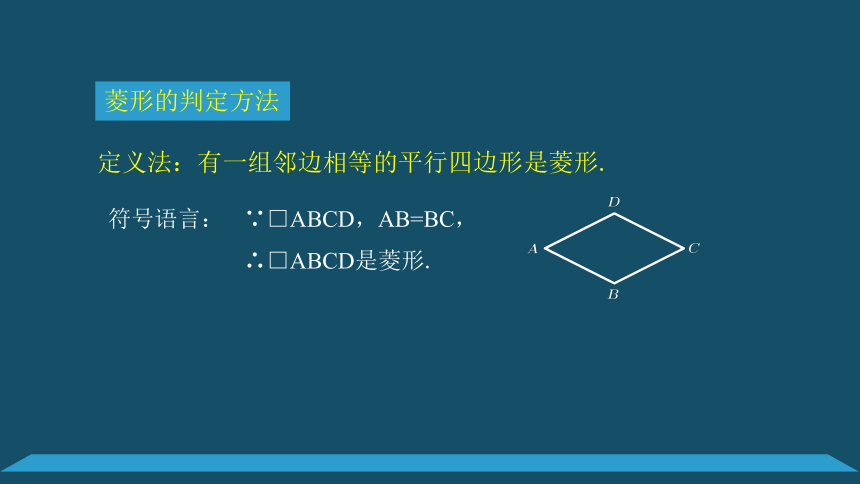
菱形的判定方法
定义法:有一组邻边相等的平行四边形是菱形.
∵□ABCD,AB=BC,
∴□ABCD是菱形.
符号语言:
菱形的特殊性质
菱形的四条边都相等
菱形的对角线互相垂直,并且每一条对角线平分一组对角
菱形的判定
问题2:
你能得到哪些关于菱形判定的猜想?
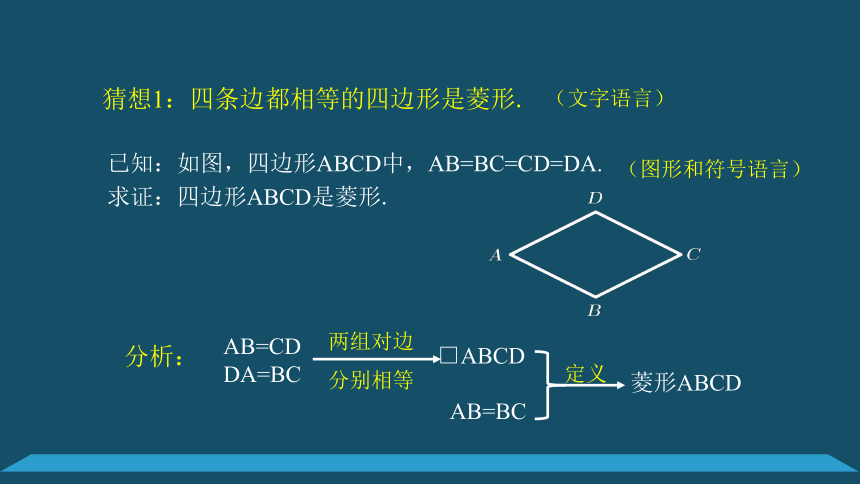
已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
两组对边
分别相等
定义
猜想1:四条边都相等的四边形是菱形.
(文字语言)
(图形和符号语言)
AB=CD
DA=BC
分析:
□ABCD
AB=BC
菱形ABCD
证明:∵
AB=CD,DA=BC
,
∴四边形ABCD是平行四边形.
又∵
AB=BC,
∴平行四边形ABCD是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
猜想1:四条边都相等的四边形是菱形.
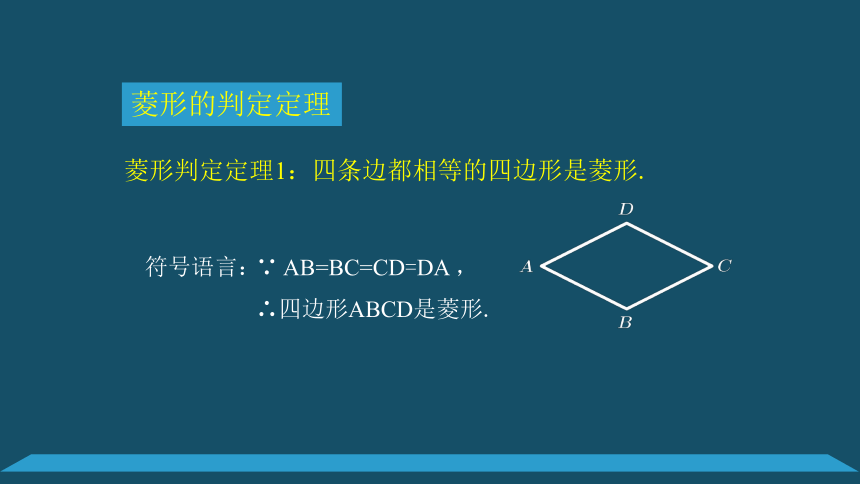
菱形判定定理1:四条边都相等的四边形是菱形.
菱形的判定定理
符号语言:
∵
AB=BC=CD=DA
,
∴四边形ABCD是菱形.
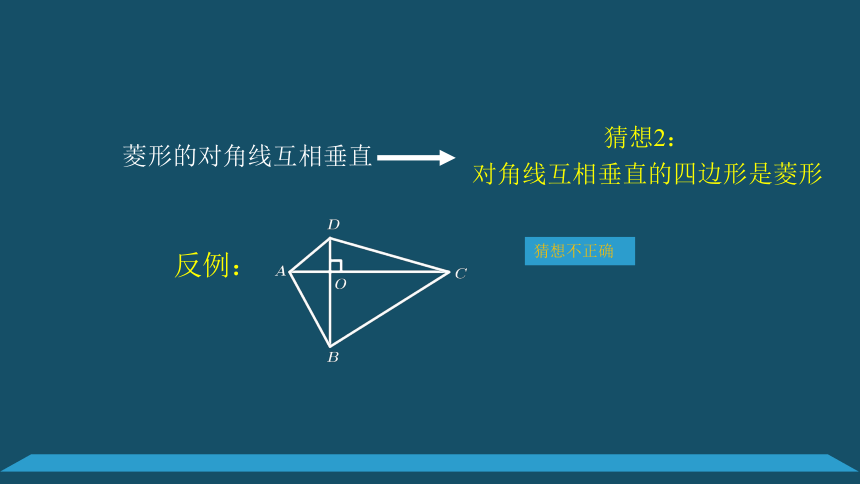
菱形的对角线互相垂直
猜想2:
对角线互相垂直的四边形是菱形
反例:
猜想不正确
猜想2:
对角线互相垂直的平行四边形是菱形
你能证明所得的猜想吗?
菱形的对角线互相垂直
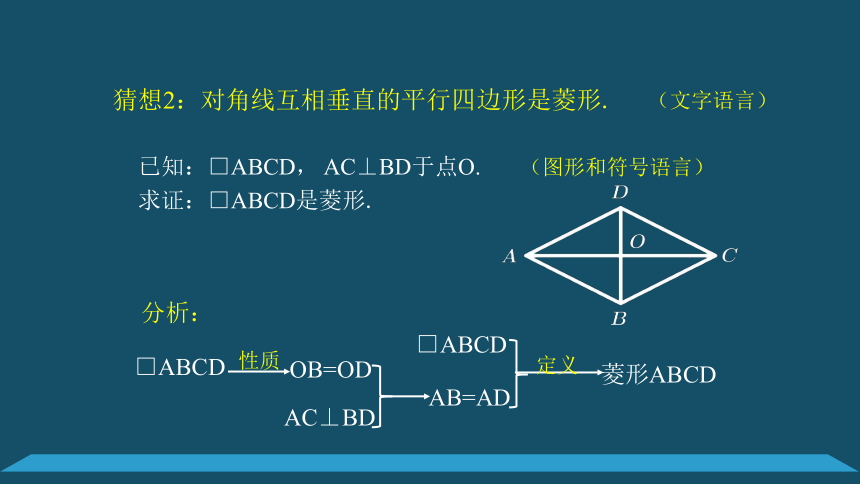
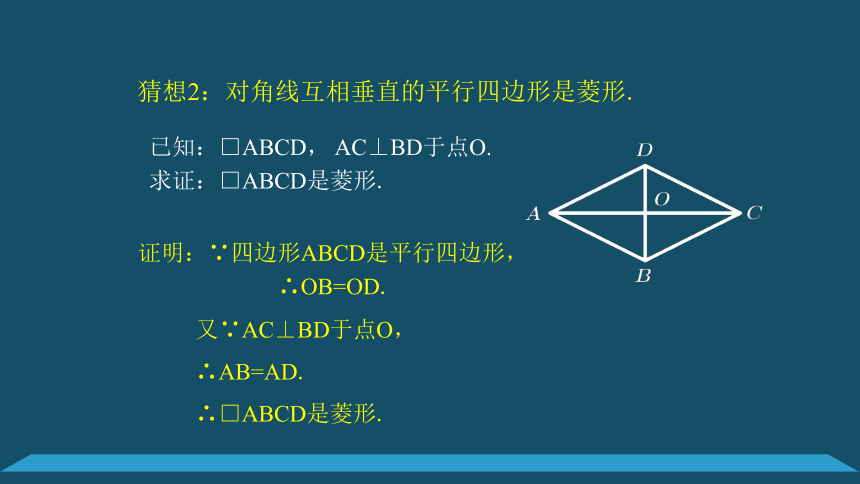
猜想2:对角线互相垂直的平行四边形是菱形.
已知:□ABCD,
AC⊥BD于点O.
求证:□ABCD是菱形.
□ABCD
分析:
OB=OD
AC⊥BD
AB=AD
□ABCD
菱形ABCD
性质
定义
(文字语言)
(图形和符号语言)
证明:∵四边形ABCD是平行四边形,
∴OB=OD.
又∵AC⊥BD于点O,
∴AB=AD.
∴□ABCD是菱形.
猜想2:对角线互相垂直的平行四边形是菱形.
已知:□ABCD,
AC⊥BD于点O.
求证:□ABCD是菱形.
菱形判定定理2:对角线互相垂直的平行四边形是菱形.
∵□ABCD,
AC⊥BD于点O,
∴□ABCD是菱形.
符号语言:
菱形的判定定理
菱形的判定方法
定义法
菱形判定定理1
菱形判定定理2
有一组邻边相等的平行四边形是菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
实际应用
木工师傅在做菱形的窗格时,只要保证窗格的四条边框一样长就行了,你能说明其中的道理吗?
依据:四条边都相等的四边形是菱形.
练习1
如图,若使□ABCD为菱形,则需要添加的
条件是_____________________.
应用练习
巩固判定
AB=BC
或
AC⊥BD
平行四边形
菱形
有一组邻边相等
或对角线互相垂直
分析:
练习2
已知,如图,AB=AD,分别以点B,D为圆心,AB长为半径作弧,两弧交于点C,连接BC,CD.得到的四边形ABCD是_______.
菱形
AB=AD
AB=BC=CD=AD
BC=AB
CD=AB
作图
分析:
菱形ABCD
如图,已知线段AB,分别以点A,B为圆心,大于
AB的同样长为半径作弧,两弧分别交于点M,N,连接AM,BM,AN,BN.
得到的四边形ANBM是菱形.
依据:四条边都相等的四边形是菱形.
AM=BM=AN=BN=半径
作图
分析:
菱形ANBM
练习4
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
练习5
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
练习5
分析:
AB=BC=CD=DA
菱形ABCD
操作
依据:四条边都相等的四边形是菱形.
A
B
C
D
O
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
AC⊥BD
菱形ABCD
练习5
方法2
OA=OC,OB=OD
□ABCD
分析:
A
B
C
D
O
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
分析:
□ABCD
∠3=∠4
△AOE≌△COF(ASA)
AD∥BC
∠1=
∠2
1
2
3
4
垂直平分线
AO=CO
EO=FO
□AFCE
EF⊥AC
菱形AFCE
AO=CO
∵□ABCD,∴AD∥BC.∴∠1=
∠2.
又∵∠3=
∠4,AO=CO,
解:四边形AFCE是菱形.
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
∴△AOE≌△COF.
∴EO=FO.
∴四边形AFCE是平行四边形.
又∵
EF⊥AC,∴□AFCE是菱形.
对角线
互相垂直
菱形
四边形
平行
四边形
对角线
互相平分
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
□ABCD
AD∥BC
垂直
平分线
∠1=
∠3
∠1=
∠2
∠3=
∠2
方法2
分析:
∠5=
∠4
AE=CE
AF=CF
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
∠5=
∠4
CO=CO
△COE≌△COF(ASA)
CE=CF
AE=CE=CF=FA
菱形AFCE
AF=CF
,AE=CE
∵□ABCD,∴AD∥BC.∴∠1=
∠2.
∵EF是线段AC的垂直平分线,
方法2
解:四边形AFCE是菱形.
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
∴∠5=
∠4,AE=CE,AF=CF.
∵
AE=CE
,∴∠1=∠3.∴∠3=∠2.
∴△COE≌△COF.
∴CE=CF.∴AE=CE
=CF=FA.
∴四边形AFCE是菱形.
菱形
四边形
四条边都相等
菱形
四边形
四条边都相等
如何由四边形得菱形?
有一组邻边相等
或
对角线互相垂直
平行四边形
或
两组对边分别相等
或
一组对边平行且相等
或
对角线互相平分
两组对边分别平行
菱形
如何由平行四边形得菱形?
有一组邻边相等
或
对角线互相垂直
平行四边形
变式
如图,已知□ABCD,点E,F分别是边AD,BC上的点,且DE=BF,
EF⊥AC,四边形AFCE是菱形吗?为什么?
AE∥CF
□AFCE
EF⊥AC
菱形AFCE
□ABCD
AD∥BC
AD=BC
分析:
DE=BF
AE=CF
解:四边形AFCE是菱形.
∵□ABCD,∴AD∥BC,
AD=BC.
∵DE=BF,∴AE=CF.
变式
如图,已知□ABCD,点E,F分别是边AD,BC上的点,且DE=BF,
EF⊥AC,四边形AFCE是菱形吗?为什么?
∵AE=CF,AE∥CF,
∴四边形AFCE是平行四边形.
又∵
EF⊥AC
,
∴□AFCE是菱形.
一组对边
平行且相等
对角线
互相垂直
菱形
四边形
平行
四边形
练习:如图,两条等宽的长方形纸条交叉放在一起,重合的部分构成的四边形ABCD是菱形吗?为什么?
分析:
AB∥CD
AD∥BC
□ABCD
作AE⊥BC于点E,AF⊥DC于点F,
∠ABE=∠ADF
等宽
AE=AF
练习:如图,两条等宽的长方形纸条交叉放在一起,重合的部分构成的四边形ABCD是菱形吗?为什么?
△ABE≌△ADF
AB=AD
菱形ABCD
∠ABE=∠ADF
∠AEB=∠AFD
□ABCD
1.本节课你学习了什么知识?
课堂总结
菱形的判定方法
定义法
菱形判定定理1
菱形判定定理2
有一组邻边相等的平行四边形是菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
课堂总结
2.本节课所采用的研究方法是什么?
定义
性质
判定
逆向猜想
(1)由定义直接得判定.
(2)由性质猜想得判定.
定义法
课堂总结
3.本节课你感悟到的解题思路是什么?
4.本节课的研究过程给你的学习带来什么启示?
菱形
四边形
四条边都相等
有一组邻边相等
或
对角线互相垂直
平行四边形
或
两组对边分别相等
或
一组对边平行且相等
或
对角线互相平分
两组对边分别平行
课后作业
2.如图,□ABCD的对角线AC与BD交于点O,
AB=
,
AO=2,OB=1.
(1)AC,BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
1.画一个菱形,使它的两条对角线长分别是6cm和8cm.
课后作业
3.如图,AD平分∠BAC,交线段BC于点D,DE∥AC交
AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.
再
见
18.2.2.2
菱形的判定
学习目标
1
2
3
掌握菱形的三种判定方法
渗透类比思想,体会研究图形判定的一般思路
在探究和应用的过程中提高几何直观能力和推理能力
学习重难点
重点
难点
菱形的判定及应用
菱形的判定的探索及解题思路的体会
菱形的判定方法
定义法:有一组邻边相等的平行四边形是菱形.
∵□ABCD,AB=BC,
∴□ABCD是菱形.
符号语言:
菱形的特殊性质
菱形的四条边都相等
菱形的对角线互相垂直,并且每一条对角线平分一组对角
菱形的判定
问题2:
你能得到哪些关于菱形判定的猜想?
已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
两组对边
分别相等
定义
猜想1:四条边都相等的四边形是菱形.
(文字语言)
(图形和符号语言)
AB=CD
DA=BC
分析:
□ABCD
AB=BC
菱形ABCD
证明:∵
AB=CD,DA=BC
,
∴四边形ABCD是平行四边形.
又∵
AB=BC,
∴平行四边形ABCD是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
猜想1:四条边都相等的四边形是菱形.
菱形判定定理1:四条边都相等的四边形是菱形.
菱形的判定定理
符号语言:
∵
AB=BC=CD=DA
,
∴四边形ABCD是菱形.
菱形的对角线互相垂直
猜想2:
对角线互相垂直的四边形是菱形
反例:
猜想不正确
猜想2:
对角线互相垂直的平行四边形是菱形
你能证明所得的猜想吗?
菱形的对角线互相垂直
猜想2:对角线互相垂直的平行四边形是菱形.
已知:□ABCD,
AC⊥BD于点O.
求证:□ABCD是菱形.
□ABCD
分析:
OB=OD
AC⊥BD
AB=AD
□ABCD
菱形ABCD
性质
定义
(文字语言)
(图形和符号语言)
证明:∵四边形ABCD是平行四边形,
∴OB=OD.
又∵AC⊥BD于点O,
∴AB=AD.
∴□ABCD是菱形.
猜想2:对角线互相垂直的平行四边形是菱形.
已知:□ABCD,
AC⊥BD于点O.
求证:□ABCD是菱形.
菱形判定定理2:对角线互相垂直的平行四边形是菱形.
∵□ABCD,
AC⊥BD于点O,
∴□ABCD是菱形.
符号语言:
菱形的判定定理
菱形的判定方法
定义法
菱形判定定理1
菱形判定定理2
有一组邻边相等的平行四边形是菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
实际应用
木工师傅在做菱形的窗格时,只要保证窗格的四条边框一样长就行了,你能说明其中的道理吗?
依据:四条边都相等的四边形是菱形.
练习1
如图,若使□ABCD为菱形,则需要添加的
条件是_____________________.
应用练习
巩固判定
AB=BC
或
AC⊥BD
平行四边形
菱形
有一组邻边相等
或对角线互相垂直
分析:
练习2
已知,如图,AB=AD,分别以点B,D为圆心,AB长为半径作弧,两弧交于点C,连接BC,CD.得到的四边形ABCD是_______.
菱形
AB=AD
AB=BC=CD=AD
BC=AB
CD=AB
作图
分析:
菱形ABCD
如图,已知线段AB,分别以点A,B为圆心,大于
AB的同样长为半径作弧,两弧分别交于点M,N,连接AM,BM,AN,BN.
得到的四边形ANBM是菱形.
依据:四条边都相等的四边形是菱形.
AM=BM=AN=BN=半径
作图
分析:
菱形ANBM
练习4
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
练习5
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
练习5
分析:
AB=BC=CD=DA
菱形ABCD
操作
依据:四条边都相等的四边形是菱形.
A
B
C
D
O
将一张矩形的纸进行对折,旋转90o后再对折,然后沿着图中所示虚线剪下并打开,打开的这个图形是什么图形呢?说明你的理由.
AC⊥BD
菱形ABCD
练习5
方法2
OA=OC,OB=OD
□ABCD
分析:
A
B
C
D
O
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
分析:
□ABCD
∠3=∠4
△AOE≌△COF(ASA)
AD∥BC
∠1=
∠2
1
2
3
4
垂直平分线
AO=CO
EO=FO
□AFCE
EF⊥AC
菱形AFCE
AO=CO
∵□ABCD,∴AD∥BC.∴∠1=
∠2.
又∵∠3=
∠4,AO=CO,
解:四边形AFCE是菱形.
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
∴△AOE≌△COF.
∴EO=FO.
∴四边形AFCE是平行四边形.
又∵
EF⊥AC,∴□AFCE是菱形.
对角线
互相垂直
菱形
四边形
平行
四边形
对角线
互相平分
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
□ABCD
AD∥BC
垂直
平分线
∠1=
∠3
∠1=
∠2
∠3=
∠2
方法2
分析:
∠5=
∠4
AE=CE
AF=CF
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
∠5=
∠4
CO=CO
△COE≌△COF(ASA)
CE=CF
AE=CE=CF=FA
菱形AFCE
AF=CF
,AE=CE
∵□ABCD,∴AD∥BC.∴∠1=
∠2.
∵EF是线段AC的垂直平分线,
方法2
解:四边形AFCE是菱形.
例1
如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F,四边形AFCE是菱形吗?为什么?
1
2
3
4
∴∠5=
∠4,AE=CE,AF=CF.
∵
AE=CE
,∴∠1=∠3.∴∠3=∠2.
∴△COE≌△COF.
∴CE=CF.∴AE=CE
=CF=FA.
∴四边形AFCE是菱形.
菱形
四边形
四条边都相等
菱形
四边形
四条边都相等
如何由四边形得菱形?
有一组邻边相等
或
对角线互相垂直
平行四边形
或
两组对边分别相等
或
一组对边平行且相等
或
对角线互相平分
两组对边分别平行
菱形
如何由平行四边形得菱形?
有一组邻边相等
或
对角线互相垂直
平行四边形
变式
如图,已知□ABCD,点E,F分别是边AD,BC上的点,且DE=BF,
EF⊥AC,四边形AFCE是菱形吗?为什么?
AE∥CF
□AFCE
EF⊥AC
菱形AFCE
□ABCD
AD∥BC
AD=BC
分析:
DE=BF
AE=CF
解:四边形AFCE是菱形.
∵□ABCD,∴AD∥BC,
AD=BC.
∵DE=BF,∴AE=CF.
变式
如图,已知□ABCD,点E,F分别是边AD,BC上的点,且DE=BF,
EF⊥AC,四边形AFCE是菱形吗?为什么?
∵AE=CF,AE∥CF,
∴四边形AFCE是平行四边形.
又∵
EF⊥AC
,
∴□AFCE是菱形.
一组对边
平行且相等
对角线
互相垂直
菱形
四边形
平行
四边形
练习:如图,两条等宽的长方形纸条交叉放在一起,重合的部分构成的四边形ABCD是菱形吗?为什么?
分析:
AB∥CD
AD∥BC
□ABCD
作AE⊥BC于点E,AF⊥DC于点F,
∠ABE=∠ADF
等宽
AE=AF
练习:如图,两条等宽的长方形纸条交叉放在一起,重合的部分构成的四边形ABCD是菱形吗?为什么?
△ABE≌△ADF
AB=AD
菱形ABCD
∠ABE=∠ADF
∠AEB=∠AFD
□ABCD
1.本节课你学习了什么知识?
课堂总结
菱形的判定方法
定义法
菱形判定定理1
菱形判定定理2
有一组邻边相等的平行四边形是菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
课堂总结
2.本节课所采用的研究方法是什么?
定义
性质
判定
逆向猜想
(1)由定义直接得判定.
(2)由性质猜想得判定.
定义法
课堂总结
3.本节课你感悟到的解题思路是什么?
4.本节课的研究过程给你的学习带来什么启示?
菱形
四边形
四条边都相等
有一组邻边相等
或
对角线互相垂直
平行四边形
或
两组对边分别相等
或
一组对边平行且相等
或
对角线互相平分
两组对边分别平行
课后作业
2.如图,□ABCD的对角线AC与BD交于点O,
AB=
,
AO=2,OB=1.
(1)AC,BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
1.画一个菱形,使它的两条对角线长分别是6cm和8cm.
课后作业
3.如图,AD平分∠BAC,交线段BC于点D,DE∥AC交
AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.
再
见
