2020-2021学年八年级数学人教版下册19.1变量与函数(共21张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册19.1变量与函数(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 229.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 07:05:12 | ||
图片预览






文档简介
(共21张PPT)
变量与函数
大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢?
数学上常用变量与函数来刻画各种运动变化.
问题1:汽车以60
km/h的速度匀速行驶,行驶时间为t
h.
(1).填写下表,s的值随t的值的变化而变化吗?
(2).在以上这个过程中,不变化的量是
.
变化的量是
.?
t/h
1
2
3
4
5
s/km
t/h
1
2
3
4
5
s/km
60
120
180
240
300
行驶里程s与时间t
速度60
km/h
(
3).试用含t的式子表示s.
s=60t.
s随t的增大而增大.
一.变量与常量
问题2:你见过水中涟漪吗?如图所示,圆形水波慢慢的扩大.在这一过程中,圆的面积S分别为多少?S的值随r的值的变化而变化吗?
S与r之间满足下列关系:S= .?
πr2
一.变量与常量
其中,不变的量是
,变化的量是
.?
π
r
,S
y随x的增大而增大.
问题3:用10
m长的绳子围成一个矩形,当矩形的一边长为xm时,它的邻边长y分别为多少?y的值随x的值的变化而变化吗?
y=5-x
y随x的增大而减小.
5
x,
y
一.变量与常量
小结
变量和常量的定义:在某个变化过程中,我们称数值发生变化的量为变量;
数值始终不变的量叫做常量.
s=60t
S=πr2
y=5-x
学习变量后,我们会发现变量的变化并不是孤立地发生,而是存在一些互相联系,当其中一个变量取定一个值时,另一个变量就随之确定一个值.
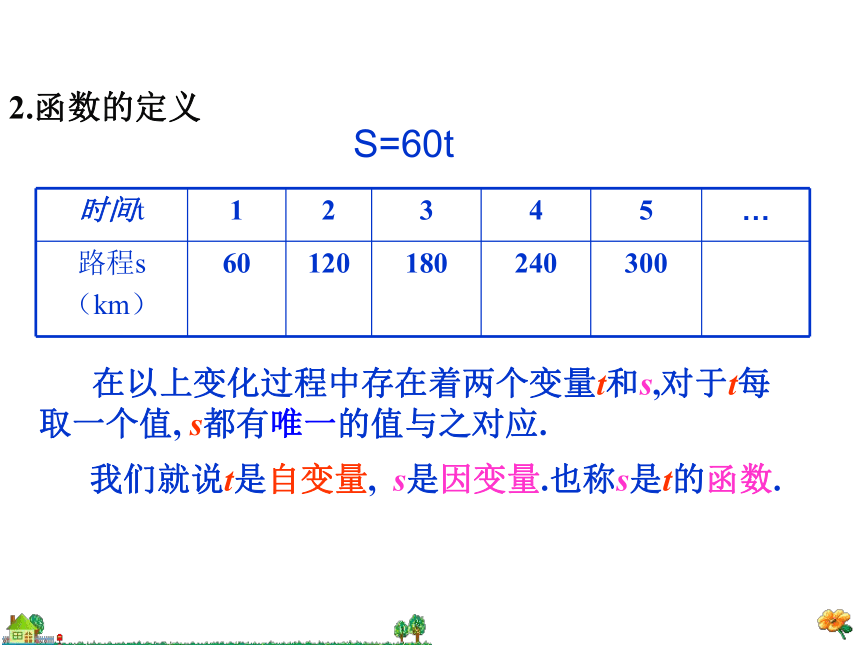
S=60t
在以上变化过程中存在着两个变量t和s,对于t每取一个值,
s都有唯一的值与之对应.
我们就说t是自变量,
s是因变量.也称s是t的函数.
时间t
1
2
3
4
5
…
路程s
(km)
60
120
180
240
300
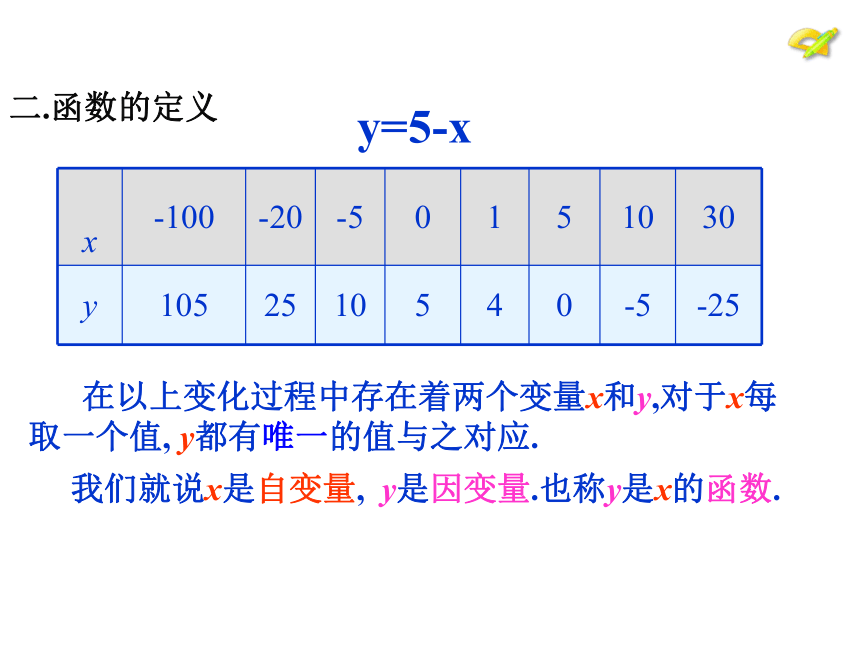
2.函数的定义
x
-100
-20
-5
0
1
5
10
30
y
105
25
10
5
4
0
-5
-25
y=5-x
二.函数的定义
在以上变化过程中存在着两个变量x和y,对于x每取一个值,
y都有唯一的值与之对应.
我们就说x是自变量,
y是因变量.也称y是x的函数.
x
-10
-5
-1
0
1
5
10
30
y
100
25
1
0
1
25
100
900
二.函数的定义
在以上变化过程中存在着两个变量x和y,对于x每取一个值,
y都有唯一的值与之对应.
我们就说x是自变量,
y是因变量.也称y是x的函数.
函数的定义:
一般地,在一个变化过程中,如果有两个变量
x
与
y,并且对于
x
的每一个确定的值,y
都有唯一确定的值
与其对应,那么我们就说
x
是自变量,
y
是因变量,此时也称y
是
x
的函数.
如果当
x
=a
时,对应的
y
=b,
那么
b
叫做当自变量的值为
a
时的函数值.
二.函数的定义
因变量与自变量的对应关系又叫函数关系.
1.每张门票的售价为10元,门票收入y(元)和门票x(张)的关系是y=10x
;
常量是____,变量是______;其中自变量是______,______是______的函数;
根据函数概念填空
检测反馈
2.汽车以60
km/h的速度匀速行驶,行驶时间为t
h.
t/h
1
2
3
4
5
s/km
t/h
1
2
3
4
5
s/km
60
120
180
240
300
在这个变化过程中,常量是____,变量是______;其中自变量是______,______是______的函数;
3.从某地一天的气温变化图中看到的时间与温度之间的关系。
在这个变化过程中,自变量____,
____是_____的函数;
解析式、表格、图象
通过上面的例子,你发现可以用哪些形式来表示一个函数呢?
函数的三种表示方法:
解析法、列表法、图象法
16
三.自变量的取值范围
使函数有意义的自变量的取值的
全体,叫做函数自变量的取值范围。
17
例1
求下列函数中自变量x的取值范围
分析:用数学式子表示的函数,一般来说,自变量只能取使式子有意义的值。
(3)由题意得:
,
解得
解:(1)由题意得:
x取任意实数
(2)由题意得:
解得
x≠1
三.自变量的取值范围
19
1、当函数解析式是只含有一个自变量的整式时:
2、当函数解析式是分式时:
3、当函数解析式是二次根式时:
4、当自变量零指数或负指数时:
5、如果一个函数解析式中同时含有几个代数式时:
全体实数
使分母不为零的实数
使被开方数不小于零的实数
三.自变量的取值范围
小结
底数不等于零。
各代数式自变量
取值范围的公共部分。
20
4.实际问题的函数解析式中自变量取值范围:
函数自变量的取值范围既要使实际问题有意义,又要同时满足解析式的数学意义。
实际问题有意义主要指的是:
(1)问题的实际背景(例如自变量表示人数时,应为非负整数等)
(2)
保证几何图形存在(例如等腰三角形底角大于0度小于90度等)
21
小结:知识梳理
1.变量与常量
2.函数的定义
3.自变量的取值范围
4.实际问题的函数解析式中自变量取值范围:
变量与函数
大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢?
数学上常用变量与函数来刻画各种运动变化.
问题1:汽车以60
km/h的速度匀速行驶,行驶时间为t
h.
(1).填写下表,s的值随t的值的变化而变化吗?
(2).在以上这个过程中,不变化的量是
.
变化的量是
.?
t/h
1
2
3
4
5
s/km
t/h
1
2
3
4
5
s/km
60
120
180
240
300
行驶里程s与时间t
速度60
km/h
(
3).试用含t的式子表示s.
s=60t.
s随t的增大而增大.
一.变量与常量
问题2:你见过水中涟漪吗?如图所示,圆形水波慢慢的扩大.在这一过程中,圆的面积S分别为多少?S的值随r的值的变化而变化吗?
S与r之间满足下列关系:S= .?
πr2
一.变量与常量
其中,不变的量是
,变化的量是
.?
π
r
,S
y随x的增大而增大.
问题3:用10
m长的绳子围成一个矩形,当矩形的一边长为xm时,它的邻边长y分别为多少?y的值随x的值的变化而变化吗?
y=5-x
y随x的增大而减小.
5
x,
y
一.变量与常量
小结
变量和常量的定义:在某个变化过程中,我们称数值发生变化的量为变量;
数值始终不变的量叫做常量.
s=60t
S=πr2
y=5-x
学习变量后,我们会发现变量的变化并不是孤立地发生,而是存在一些互相联系,当其中一个变量取定一个值时,另一个变量就随之确定一个值.
S=60t
在以上变化过程中存在着两个变量t和s,对于t每取一个值,
s都有唯一的值与之对应.
我们就说t是自变量,
s是因变量.也称s是t的函数.
时间t
1
2
3
4
5
…
路程s
(km)
60
120
180
240
300
2.函数的定义
x
-100
-20
-5
0
1
5
10
30
y
105
25
10
5
4
0
-5
-25
y=5-x
二.函数的定义
在以上变化过程中存在着两个变量x和y,对于x每取一个值,
y都有唯一的值与之对应.
我们就说x是自变量,
y是因变量.也称y是x的函数.
x
-10
-5
-1
0
1
5
10
30
y
100
25
1
0
1
25
100
900
二.函数的定义
在以上变化过程中存在着两个变量x和y,对于x每取一个值,
y都有唯一的值与之对应.
我们就说x是自变量,
y是因变量.也称y是x的函数.
函数的定义:
一般地,在一个变化过程中,如果有两个变量
x
与
y,并且对于
x
的每一个确定的值,y
都有唯一确定的值
与其对应,那么我们就说
x
是自变量,
y
是因变量,此时也称y
是
x
的函数.
如果当
x
=a
时,对应的
y
=b,
那么
b
叫做当自变量的值为
a
时的函数值.
二.函数的定义
因变量与自变量的对应关系又叫函数关系.
1.每张门票的售价为10元,门票收入y(元)和门票x(张)的关系是y=10x
;
常量是____,变量是______;其中自变量是______,______是______的函数;
根据函数概念填空
检测反馈
2.汽车以60
km/h的速度匀速行驶,行驶时间为t
h.
t/h
1
2
3
4
5
s/km
t/h
1
2
3
4
5
s/km
60
120
180
240
300
在这个变化过程中,常量是____,变量是______;其中自变量是______,______是______的函数;
3.从某地一天的气温变化图中看到的时间与温度之间的关系。
在这个变化过程中,自变量____,
____是_____的函数;
解析式、表格、图象
通过上面的例子,你发现可以用哪些形式来表示一个函数呢?
函数的三种表示方法:
解析法、列表法、图象法
16
三.自变量的取值范围
使函数有意义的自变量的取值的
全体,叫做函数自变量的取值范围。
17
例1
求下列函数中自变量x的取值范围
分析:用数学式子表示的函数,一般来说,自变量只能取使式子有意义的值。
(3)由题意得:
,
解得
解:(1)由题意得:
x取任意实数
(2)由题意得:
解得
x≠1
三.自变量的取值范围
19
1、当函数解析式是只含有一个自变量的整式时:
2、当函数解析式是分式时:
3、当函数解析式是二次根式时:
4、当自变量零指数或负指数时:
5、如果一个函数解析式中同时含有几个代数式时:
全体实数
使分母不为零的实数
使被开方数不小于零的实数
三.自变量的取值范围
小结
底数不等于零。
各代数式自变量
取值范围的公共部分。
20
4.实际问题的函数解析式中自变量取值范围:
函数自变量的取值范围既要使实际问题有意义,又要同时满足解析式的数学意义。
实际问题有意义主要指的是:
(1)问题的实际背景(例如自变量表示人数时,应为非负整数等)
(2)
保证几何图形存在(例如等腰三角形底角大于0度小于90度等)
21
小结:知识梳理
1.变量与常量
2.函数的定义
3.自变量的取值范围
4.实际问题的函数解析式中自变量取值范围:
