2020-2021学年八年级数学苏科版下册《 11.2 反比例函数的图象和性质》强化提优试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学苏科版下册《 11.2 反比例函数的图象和性质》强化提优试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 14:35:57 | ||
图片预览



文档简介
苏科版八年级数学下册《
11.2
反比例函数的图象和性质》强化提优试卷(2)
(时间:90分钟
满分:120分)
1.选择题(共15题;共30分)
1.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是(
)
A.
y3B.
y2C.
y1D.
y12.如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=在第一象限内的图象与△ABC有交点,则k的取值范围是(
)
A.
1≤k≤4
B.
2≤k≤8
C.
2≤k≤16
D.
8≤k≤16
第2题图
第3题图
第5题图
3.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是(
)
A.
1B.
1≤x≤3
C.
x>1
D.
x<3
4.已知A(x1,y1),B(x2,y2)是反比例函数y=(k≠0)图象上的两个点,当x1<x2<0时,y1>y2,则一次函数y=kx-k的图象不经过(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
5.如图所示,已知点A是反比例函数y
=
(k
>
0)的图象上的一点,AB⊥y轴于点B,P是x轴上任意一点,若△ABP的面积为3,则k的值为(
)
A.3
B.
-
3
C.6
D.
-
6
6.已知y
=
y1+
y2,其中y与成反比例且比例系数为k1,y2与x成正比例且比例系数为k2.若x
=-
1时,y
=
0,则k1,k2的关系为(
)
A.k1
+
k2
=
0
B.k1k2
=
1
C.k1k2
=
-
1
D.k1
=
k2
7.已知点A在函数y1
=
-
(x
>
0)的图象上,点B在直线y2
=
kx
+
1
+
k(k为常数,且k≥0)上.若A,B两点关于原点对称,则陈点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为(
A
)
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
8.关于反比例函数,下列说法中错误的是( )
A.当时,随的增大而增大
B.图象位于第二、四象限
C.点在函数图象上
D.当时,
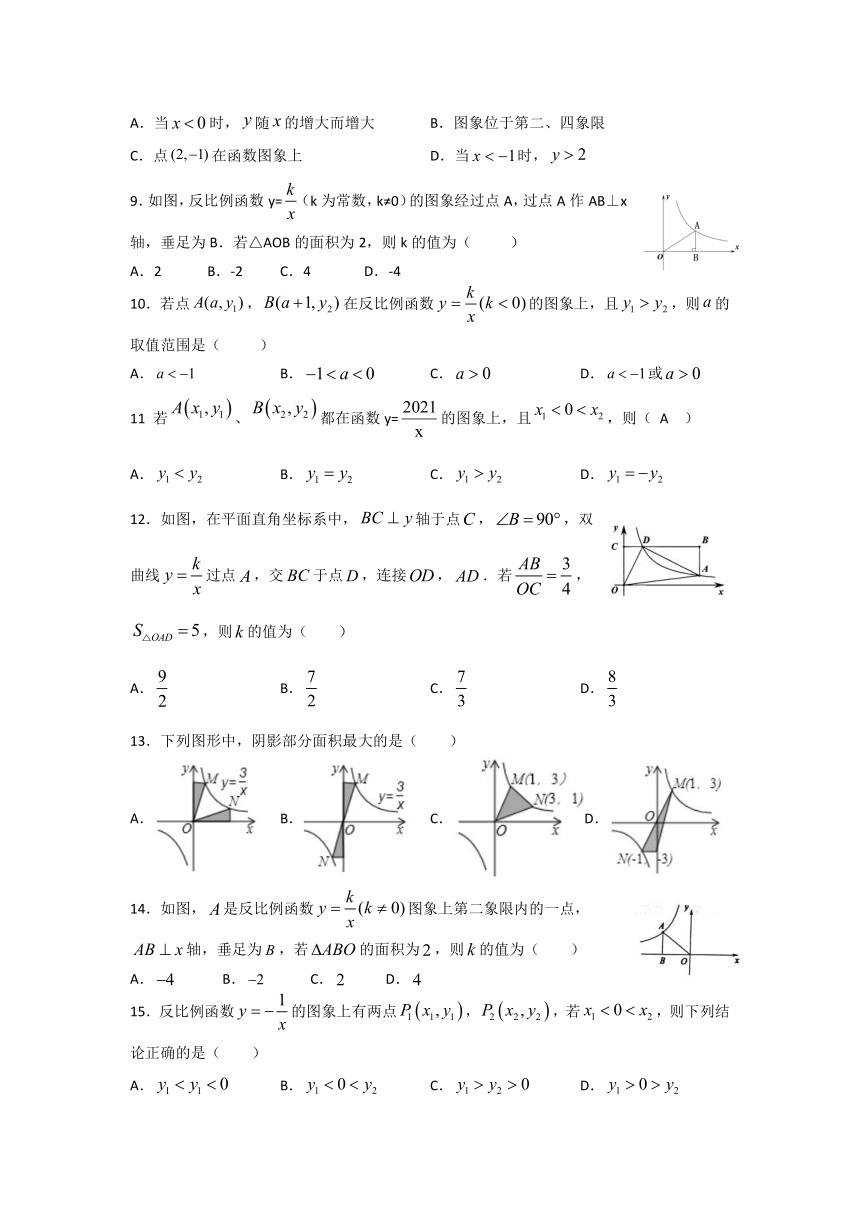
9.如图,反比例函数y=(k为常数,k≠0)的图象经过点A,过点A作AB⊥x轴,垂足为B.若△AOB的面积为2,则k的值为(
)
A.2
B.-2
C.4
D.-4
10.若点,在反比例函数的图象上,且,则的取值范围是(
)
A.
B.
C.
D.或
11
若、都在函数y=的图象上,且,则(
A
)
A.
B.
C.
D.
12.如图,在平面直角坐标系中,轴于点,,双曲线过点,交于点,连接,.若,,则的值为(
)
A.
B.
C.
D.
13.下列图形中,阴影部分面积最大的是(
)
A.
B.
C.D.
14.如图,是反比例函数图象上第二象限内的一点,轴,垂足为,若的面积为,则的值为(
)
A.
B.
C.
D.
15.反比例函数的图象上有两点,,若,则下列结论正确的是(
)
A.
B.
C.
D.
2.填空题(共10题;共20分)
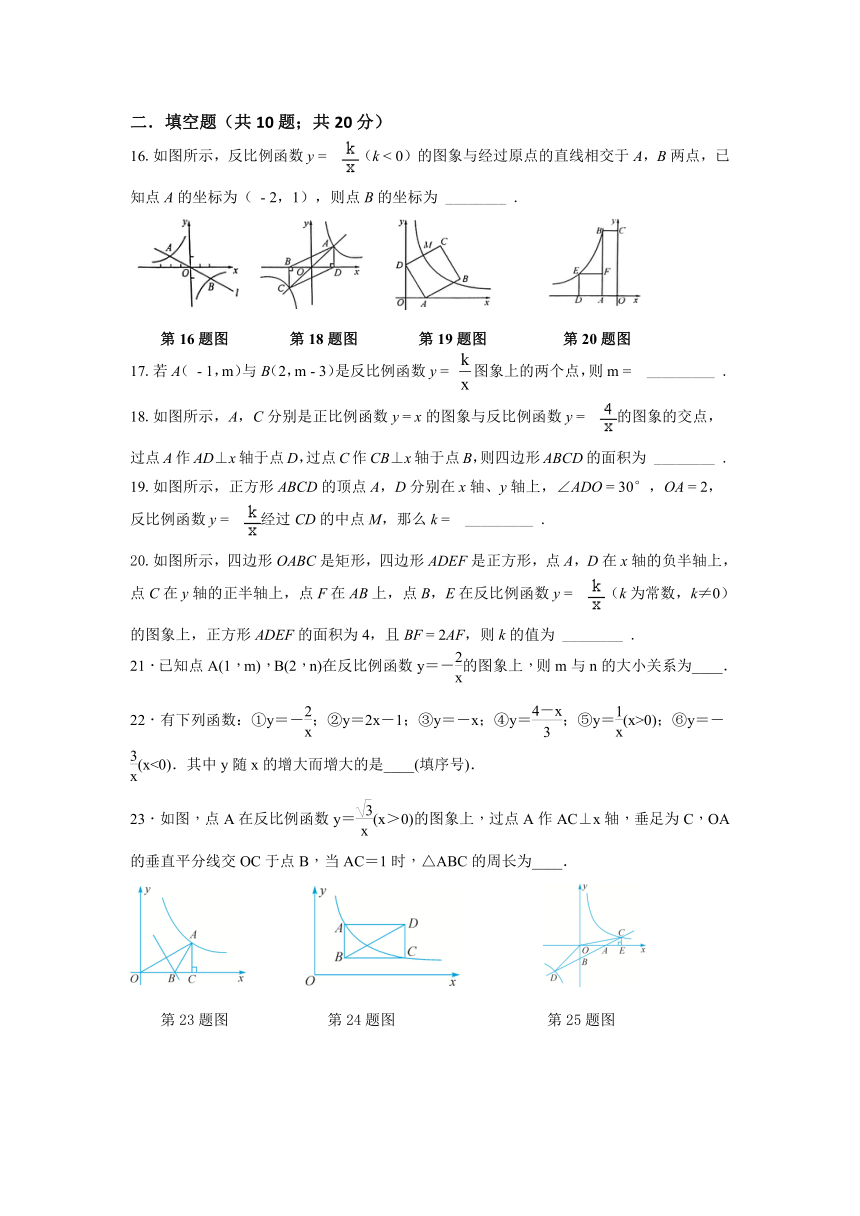
16.如图所示,反比例函数y
=
(k
<
0)的图象与经过原点的直线相交于A,B两点,已知点A的坐标为(
-
2,1),则点B的坐标为
________
.
第16题图
第18题图
第19题图
第20题图
17.若A(
-
1,m)与B(2,m
-
3)是反比例函数y
=
图象上的两个点,则m
=
_________
.
18.如图所示,A,C分别是正比例函数y
=
x的图象与反比例函数y
=
的图象的交点,过点A作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD的面积为
________
.
19.如图所示,正方形ABCD的顶点A,D分别在x轴、y轴上,∠ADO
=
30°,OA
=
2,反比例函数y
=
经过CD的中点M,那么k
=
_________
.
20.如图所示,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y
=
(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF
=
2AF,则k的值为
________
.
21.已知点A(1,m),B(2,n)在反比例函数y=-的图象上,则m与n的大小关系为____.
22.有下列函数:①y=-;②y=2x-1;③y=-x;④y=;⑤y=(x>0);⑥y=-(x<0).其中y随x的增大而增大的是____(填序号).
23.如图,点A在反比例函数y=(x>0)的图象上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为____.
第23题图
第24题图
第25题图
24.如图,矩形ABCD的顶点A,C都在反比例函数y=(k>0,x>0)的图象上.若顶点D的坐标为(5,3),则直线BD的函数表达式是____.
25.如图,已知在平面直角坐标系xOy中,直线y=x-1分别交x轴、y轴于点A和点B,分别交反比例函数y1=(k>0,x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD.若△COE的面积与△DOB的面积相等,则k的值为_____.
3.解答题(共9小题
共70分)
26.
(6分)作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2<y<3时,求x的取值范围;
(3)当-3<x<2时,求y的取值范围.
27.(6分)如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)在图象上取一点P,分别作x轴、y轴的垂线,垂足分别为点Q,R,四边形PQOR的面积为3,求n的值.
28.
(6分)如图,一次函数y=-x+2的图象与x轴交于点B,与反比例函数y=的图象的交点为A(-2,3).
(1)求反比例函数的表达式;
(2)过点A作AC⊥x轴,垂足为点C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.
29.
(6分)已知反比例函数y=的图象与一次函数y=3x+m的图象相交于点(1,5).
(1)
求这两个函数的解析式;
(2)
求这两个函数图象的另一个交点的坐标.
30.(6分)如图,已知双曲线y=
(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,求k的值.
31
(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)若P是y轴一点,且满足△PAB的面积是5,求P点坐标.
32.
(8分)如图,一次函数y=k1x+b(k1≠0)与反比例函数y=(k2≠0)的图象交于点A(-1,2),B(m,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
33.(8分)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.
(1)求反比例函数的表达式.
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,则点P,Q各位于哪个象限?并简要说明理由.
34.(12分)如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)的图象相交于第一、三象限内的A(3,5),B(a,-3)两点,与x轴相交于点C.
(1)求一次函数和反比例函数的表达式.
(2)在y轴上找一点P,使PB-PC最大,求PB-PC的最大值及点P的坐标[参考公式:在平面直角坐标系中,若点A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=].
(3)直接写出当y1>y2时,x的取值范围.
35.(12分)如图①,直线l1:y-=k(x-)(k<0)过定点F,且与反比例函数y=(x>0)的图象相交于A,B两点.设点A(x1,y1),B(x2,y2)(x1(1)若k=-1,求△OAB的面积S.
(2)若AB=
,求k的值.
(3)如图②,点P在函数y=(x>0)的图象上,点M在直线l2:y=-x+上,且PM∥x轴.若点N(0,2),求PM+PN的最小值,并求PM+PN取得最小值时点P的坐标.
教师样卷
1.
选择题(共15题;共30分)
1.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是(C)
A.
y3B.
y2C.
y1D.
y12.如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=在第一象限内的图象与△ABC有交点,则k的取值范围是(C)
A.
1≤k≤4
B.
2≤k≤8
C.
2≤k≤16
D.
8≤k≤16
第2题图
第3题图
第5题图
3.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是(A)
A.
1B.
1≤x≤3
C.
x>1
D.
x<3
4.已知A(x1,y1),B(x2,y2)是反比例函数y=(k≠0)图象上的两个点,当x1<x2<0时,y1>y2,则一次函数y=kx-k的图象不经过(B)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
【解】 ∵当x1<x2<0时,y1>y2,∴k>0.∵一次函数y=kx-k的图象经过点(1,0)和点(0,-k),-k<0,∴一次函数的图象不经过第二象限
5.如图所示,已知点A是反比例函数y
=
(k
>
0)的图象上的一点,AB⊥y轴于点B,P是x轴上任意一点,若△ABP的面积为3,则k的值为(
C
)
A.3
B.
-
3
C.6
D.
-
6
6.已知y
=
y1+
y2,其中y与成反比例且比例系数为k1,y2与x成正比例且比例系数为k2.若x
=-
1时,y
=
0,则k1,k2的关系为(
A
)
A.k1
+
k2
=
0
B.k1k2
=
1
C.k1k2
=
-
1
D.k1
=
k2
7.已知点A在函数y1
=
-
(x
>
0)的图象上,点B在直线y2
=
kx
+
1
+
k(k为常数,且k≥0)上.若A,B两点关于原点对称,则陈点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为(
A
)
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
8.关于反比例函数,下列说法中错误的是( D )
A.当时,随的增大而增大
B.图象位于第二、四象限
C.点在函数图象上
D.当时,
【详解】∵<0,∴当时,随的增大而增大,故A不符合题意;∵,∴图象位于第二、四象限,故B不符合题意;当时,,故C不符合题意;当时,<2,故D错误,符合题意;故答案选D.
9.如图,反比例函数y=(k为常数,k≠0)的图象经过点A,过点A作AB⊥x轴,垂足为B.若△AOB的面积为2,则k的值为(
C
)
A.2
B.-2
C.4
D.-4
【详解】∵AB⊥x轴,垂足为B.若△AOB的面积为2,∴,∴k=4,∵反比例函数图象在第一象限,∴k=4,故选:C.
10.若点,在反比例函数的图象上,且,则的取值范围是(
B
)
A.
B.
C.
D.或
解:∵反比例函数,∴图象经过第二、四象限,在每个象限内,y随x的增大而增大,①若点A、点B同在第二或第四象限,∵,∴a>a+1,此不等式无解;②若点A在第二象限,且点B在第四象限,∵,∴,
解得:;③由y1>y2,可知点A在第四象限,且点B在第二象限这种情况不可能,综上,的取值范围是,故选:B.
11
若、都在函数y=的图象上,且,则(
A
)
B.
B.
C.
D.
解:函数y=,该函数图象在第一、三象限、在每个象限内y随x的增大而减小,∵、都在函数y=的图象上,且
,∴,故选A.
12.如图,在平面直角坐标系中,轴于点,,双曲线过点,交于点,连接,.若,,则的值为(
D
)
A.
B.
C.
D.
【详解】如图:过点A作AH垂直于x轴于点H,设,轴,四边形OCBH为矩形,OH=BC,CO=BH
AH=BH-AB=4a-3a=a,点A坐标(),,双曲线与BC交于点D,点D的坐标(),,,S矩形COHB,,,
,,
S矩形COHB,整理得:,解得:,故选:D.
13.下列图形中,阴影部分面积最大的是(
C
)
A.
B.
C.D.
【详解】A、根据反比例函数系数k的几何意义,阴影部分面积和为:xy=3.B、根据反比例函数系数k的几何意义,阴影部分面积和为:
|xy|=3
.C、如图,过点M作MA⊥x轴于点A,过点N作NB⊥x轴于点B,
根据反比例函数系数k的几何意义,S△OAM=S△OBM=
|xy|=
,从而阴影部分面积和为梯形MABN的面积:
(1+3)×2=4
.D、根据M,N点的坐标以及三角形面积求法得出,阴影部分面积为:×1×6=3
.综上所述,阴影部分面积最大的是C.故选:C.
14.如图,是反比例函数图象上第二象限内的一点,轴,垂足为,若的面积为,则的值为(
A
)
A.
B.
C.
D.
【详解】根据题意得:,解得k=4或k=-4,∵函数图象在第二象限内,∴k=-4,故选:A.
15.反比例函数的图象上有两点,,若,则下列结论正确的是(
D
)
A.
B.
C.
D.
解:∵,∴xy=-1.∴x、y异号.∵x1<0<x2,∴y1>0>y2.故选:D.
2.
填空题(共10题;共20分)
16.如图所示,反比例函数y
=
(k
<
0)的图象与经过原点的直线相交于A,B两点,已知点A的坐标为(
-
2,1),则点B的坐标为
_(2,-1)________
.
第16题图
第18题图
第19题图
第20题图
17.若A(
-
1,m)与B(2,m
-
3)是反比例函数y
=
图象上的两个点,则m
=
___2______
.
18.如图所示,A,C分别是正比例函数y
=
x的图象与反比例函数y
=
的图象的交点,过点A作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD的面积为
___8______
.
19.如图所示,正方形ABCD的顶点A,D分别在x轴、y轴上,∠ADO
=
30°,OA
=
2,反比例函数y
=
经过CD的中点M,那么k
=
__+6_______
.
20.如图所示,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y
=
(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF
=
2AF,则k的值为
___-6______
.
21.已知点A(1,m),B(2,n)在反比例函数y=-的图象上,则m与n的大小关系为__m<n__.
22.有下列函数:①y=-;②y=2x-1;③y=-x;④y=;⑤y=(x>0);⑥y=-(x<0).其中y随x的增大而增大的是__②⑥__(填序号).
23.如图,点A在反比例函数y=(x>0)的图象上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为__+1__.
第23题图
第24题图
第25题图
24.如图,矩形ABCD的顶点A,C都在反比例函数y=(k>0,x>0)的图象上.若顶点D的坐标为(5,3),则直线BD的函数表达式是__y=x__.
【解】 ∵点D(5,3),点A,C都在反比例函数y=的图象上,∴点A,C,
∴点B.设直线BD的函数表达式为y=mx+n.把点D(5,3),B的坐标代入,得
f(k,3)m+n=f(k,5),))解得
n=0.))∴直线BD的函数表达式为y=x.
25如图,已知在平面直角坐标系xOy中,直线y=x-1分别交x轴、y轴于点A和点B,分别交反比例函数y1=(k>0,x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD.若△COE的面积与△DOB的面积相等,则k的值为___2__.
【解】 设点C(x1,y1),D(x2,y2).∵直线y=x-1与y轴相交于点B,∴点B(0,-1),∴OB=1.∵点C在反比例函数y1=(k>0)的图象上,∴S△COE=x1·y1=k.又∵S△BOD=S△COE=k=|x2|×1,∴x2=-k.∵点D在反比例函数y=(k>0)的图象上,∴点D(-k,-2).∵点D(-k,-2)在直线y=x-1上,∴×(-k)-1=-2,解得k=2.
3.
解答题(共9小题
共70分)
26.
(6分)作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2<y<3时,求x的取值范围;
(3)当-3<x<2时,求y的取值范围.
解:作图略(1)y=-6 (2)4<x<6 (3)y<-4或y>6
27.(6分)如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)在图象上取一点P,分别作x轴、y轴的垂线,垂足分别为点Q,R,四边形PQOR的面积为3,求n的值.
解:(1)图象的另一支位于第四象限,n<-3 (2)n=-6
28.
(6分)如图,一次函数y=-x+2的图象与x轴交于点B,与反比例函数y=的图象的交点为A(-2,3).
(1)求反比例函数的表达式;
(2)过点A作AC⊥x轴,垂足为点C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.
解:(1)反比例函数的表达式为y=- (2)设点P的坐标是(a,b).∵一次函数y=-x+2的图象与x轴交于点B,∴当y=0时,-x+2=0,解得x=4,∴点B的坐标是(4,0),即OB=4.∴BC=6.∵△PBC的面积等于18,∴×BC×|b|=18,解得|b|=6,∴b1=6,b2=-6,∴点P的坐标是(-1,6),(1,-6)
29.
(6分)已知反比例函数y=的图象与一次函数y=3x+m的图象相交于点(1,5).
(1)
求这两个函数的解析式;
(2)
求这两个函数图象的另一个交点的坐标.
解:(1)
把x=1,y=5分别代入,得k=5,m=2,∴解析式分别为y=和y=3x+2.
(2)
解方程组eq
blc{(avs4alco1(y=,
y=3x+2)),得,
eq
blc{(avs4alco1(x2=-,y2=-3)).∴另一个交点的坐标为(-,-3).
30.(6分)如图,已知双曲线y=
(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,求k的值.
解:设F(a,b),∵F在y=上,∴ab=k.∵F为AB的中点,∴B(a,2b),E(a,2b).∵S四边形OEBF=S矩形OABC
–
S△OCE
–
S△OAF∴2=a·2b-×a·2b-
a·b,即k=ab=2。
31
(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)若P是y轴一点,且满足△PAB的面积是5,求P点坐标.
解:(1)一次函数表达式为y=x+1,反比例函数表达式为y= (2)设P点坐标为(0,b),设直线y=x+1与y轴的交点为C,则C点坐标为(0,1),∴PC=|b-1|,∵S△PAC+S△PBC=S△PAB,∴|b-1|×2+|b-1|×3=5,∴|b-1|=2,∴b=3或-1,∴P点坐标为(0,3)或(0,-1)
32.
(8分)如图,一次函数y=k1x+b(k1≠0)与反比例函数y=(k2≠0)的图象交于点A(-1,2),B(m,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
解:(1)把A(-1,2)代入y=,得到k2=-2,∴反比例函数的表达式为y=-.∵B(m,-1)在y=-上,∴m=2,由题意,解得,∴一次函数的表达式为y=-x+1
(2)∵A(-1,2),B(2,-1),∴AB=3,①当PA=PB时,(n+1)2+4=(n-2)2+1,∴n=0,∵n>0,∴n=0不合题意舍弃.②当AP=AB时,22+(n+1)2=(3)2,∵n>0,∴n=-1+.③当BP=BA时,12+(n-2)2=(3)2,∵n>0,∴n=2+.综上所述,n=-1+或2+
33.(8分)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.
(1)求反比例函数的表达式.
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,则点P,Q各位于哪个象限?并简要说明理由.
【解】 (1)由题意得,点B,把点B的坐标代入y=中,得=-,解得k=-3,∴反比例函数的表达式为y=-.
(2)点P在第二象限,点Q在第四象限.理由如下:∵k=-3<0,∴反比例函数y=-在每个象限内,y随x的增大而增大.∵P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,∴点P在第二象限,点Q在第四象限.
34.(12分)如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)的图象相交于第一、三象限内的A(3,5),B(a,-3)两点,与x轴相交于点C.
(1)求一次函数和反比例函数的表达式.
(2)在y轴上找一点P,使PB-PC最大,求PB-PC的最大值及点P的坐标[参考公式:在平面直角坐标系中,若点A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=].
(3)直接写出当y1>y2时,x的取值范围.
【解】 (1)把点A(3,5)的坐标代入y2=(m≠0),得m=3×5=15,∴反比例函数的表达式为y2=.把点B(a,-3)的坐标代入y2=,得a=-5,∴点B(-5,-3).把点A(3,5),B(-5,-3)的坐标代入y=kx+b,得
-5k+b=-3,))解得
b=2.))∴一次函数的表达式为y1=x+2.
(2)在y轴上任取一点M,连结MB,MC,则MB-MC≤BC,当且仅当点M在直线BC上时取等号,∴点P为一次函数y1=x+2的图象与y轴的交点坐标.
令x=0,则y=x+2=2,∴点P(0,2).令y=x+2=0,则x=-2,∴点C(-2,0),
∴BC==3,即PB-PC的最大值为3.
(3)当y1>y2时,-5<x<0或x>3.
35.(12分)如图①,直线l1:y-=k(x-)(k<0)过定点F,且与反比例函数y=(x>0)的图象相交于A,B两点.设点A(x1,y1),B(x2,y2)(x1(1)若k=-1,求△OAB的面积S.
(2)若AB=
,求k的值.
(3)如图②,点P在函数y=(x>0)的图象上,点M在直线l2:y=-x+上,且PM∥x轴.若点N(0,2),求PM+PN的最小值,并求PM+PN取得最小值时点P的坐标.
【解】 (1)当k=-1时,直线l1:y-=-(x-),即y=-x+2.
联立解得
如解图①,设直线l1与y轴相交于点C,则点C(0,2).∴S=S△BOC-S△AOC=×2×(x2-x1)=×2×2=2.
,
(2)联立整理,得kx2+(1-k)x-1=0(k<0).∵Δ=[(1-k)]2+4k=2(1+k2)>0,∴x1,x2是方程kx2+(1-k)x-1=0(k<0)的两个根,∴∴AB==
=·=·=·=·=-.
∵AB=
,∴-=
,整理,得2k2+5k+2=0,解得k1=-2,k2=-.
(3)∵直线l1:y-=k(x-)(k<0)过定点F,∴点F(,).如解图②,设点P,则点M(-+,),∴PM=x+-.设m=x+,则PM=m-(m>).
∵PF======m-,∴PM=PF,∴PM+PN=PF+PN≥NF,∴当点P在NF上时,PM+PN取得最小值.∵点N(0,2),F(,),∴NF==2,∴PM+PN的最小值是2.由(1)易知此时点P(-1,+1).
11.2
反比例函数的图象和性质》强化提优试卷(2)
(时间:90分钟
满分:120分)
1.选择题(共15题;共30分)
1.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是(
)
A.
y3
y2
y1
y1
)
A.
1≤k≤4
B.
2≤k≤8
C.
2≤k≤16
D.
8≤k≤16
第2题图
第3题图
第5题图
3.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是(
)
A.
1
1≤x≤3
C.
x>1
D.
x<3
4.已知A(x1,y1),B(x2,y2)是反比例函数y=(k≠0)图象上的两个点,当x1<x2<0时,y1>y2,则一次函数y=kx-k的图象不经过(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
5.如图所示,已知点A是反比例函数y
=
(k
>
0)的图象上的一点,AB⊥y轴于点B,P是x轴上任意一点,若△ABP的面积为3,则k的值为(
)
A.3
B.
-
3
C.6
D.
-
6
6.已知y
=
y1+
y2,其中y与成反比例且比例系数为k1,y2与x成正比例且比例系数为k2.若x
=-
1时,y
=
0,则k1,k2的关系为(
)
A.k1
+
k2
=
0
B.k1k2
=
1
C.k1k2
=
-
1
D.k1
=
k2
7.已知点A在函数y1
=
-
(x
>
0)的图象上,点B在直线y2
=
kx
+
1
+
k(k为常数,且k≥0)上.若A,B两点关于原点对称,则陈点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为(
A
)
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
8.关于反比例函数,下列说法中错误的是( )
A.当时,随的增大而增大
B.图象位于第二、四象限
C.点在函数图象上
D.当时,
9.如图,反比例函数y=(k为常数,k≠0)的图象经过点A,过点A作AB⊥x轴,垂足为B.若△AOB的面积为2,则k的值为(
)
A.2
B.-2
C.4
D.-4
10.若点,在反比例函数的图象上,且,则的取值范围是(
)
A.
B.
C.
D.或
11
若、都在函数y=的图象上,且,则(
A
)
A.
B.
C.
D.
12.如图,在平面直角坐标系中,轴于点,,双曲线过点,交于点,连接,.若,,则的值为(
)
A.
B.
C.
D.
13.下列图形中,阴影部分面积最大的是(
)
A.
B.
C.D.
14.如图,是反比例函数图象上第二象限内的一点,轴,垂足为,若的面积为,则的值为(
)
A.
B.
C.
D.
15.反比例函数的图象上有两点,,若,则下列结论正确的是(
)
A.
B.
C.
D.
2.填空题(共10题;共20分)
16.如图所示,反比例函数y
=
(k
<
0)的图象与经过原点的直线相交于A,B两点,已知点A的坐标为(
-
2,1),则点B的坐标为
________
.
第16题图
第18题图
第19题图
第20题图
17.若A(
-
1,m)与B(2,m
-
3)是反比例函数y
=
图象上的两个点,则m
=
_________
.
18.如图所示,A,C分别是正比例函数y
=
x的图象与反比例函数y
=
的图象的交点,过点A作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD的面积为
________
.
19.如图所示,正方形ABCD的顶点A,D分别在x轴、y轴上,∠ADO
=
30°,OA
=
2,反比例函数y
=
经过CD的中点M,那么k
=
_________
.
20.如图所示,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y
=
(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF
=
2AF,则k的值为
________
.
21.已知点A(1,m),B(2,n)在反比例函数y=-的图象上,则m与n的大小关系为____.
22.有下列函数:①y=-;②y=2x-1;③y=-x;④y=;⑤y=(x>0);⑥y=-(x<0).其中y随x的增大而增大的是____(填序号).
23.如图,点A在反比例函数y=(x>0)的图象上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为____.
第23题图
第24题图
第25题图
24.如图,矩形ABCD的顶点A,C都在反比例函数y=(k>0,x>0)的图象上.若顶点D的坐标为(5,3),则直线BD的函数表达式是____.
25.如图,已知在平面直角坐标系xOy中,直线y=x-1分别交x轴、y轴于点A和点B,分别交反比例函数y1=(k>0,x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD.若△COE的面积与△DOB的面积相等,则k的值为_____.
3.解答题(共9小题
共70分)
26.
(6分)作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2<y<3时,求x的取值范围;
(3)当-3<x<2时,求y的取值范围.
27.(6分)如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)在图象上取一点P,分别作x轴、y轴的垂线,垂足分别为点Q,R,四边形PQOR的面积为3,求n的值.
28.
(6分)如图,一次函数y=-x+2的图象与x轴交于点B,与反比例函数y=的图象的交点为A(-2,3).
(1)求反比例函数的表达式;
(2)过点A作AC⊥x轴,垂足为点C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.
29.
(6分)已知反比例函数y=的图象与一次函数y=3x+m的图象相交于点(1,5).
(1)
求这两个函数的解析式;
(2)
求这两个函数图象的另一个交点的坐标.
30.(6分)如图,已知双曲线y=
(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,求k的值.
31
(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)若P是y轴一点,且满足△PAB的面积是5,求P点坐标.
32.
(8分)如图,一次函数y=k1x+b(k1≠0)与反比例函数y=(k2≠0)的图象交于点A(-1,2),B(m,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
33.(8分)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.
(1)求反比例函数的表达式.
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,则点P,Q各位于哪个象限?并简要说明理由.
34.(12分)如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)的图象相交于第一、三象限内的A(3,5),B(a,-3)两点,与x轴相交于点C.
(1)求一次函数和反比例函数的表达式.
(2)在y轴上找一点P,使PB-PC最大,求PB-PC的最大值及点P的坐标[参考公式:在平面直角坐标系中,若点A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=].
(3)直接写出当y1>y2时,x的取值范围.
35.(12分)如图①,直线l1:y-=k(x-)(k<0)过定点F,且与反比例函数y=(x>0)的图象相交于A,B两点.设点A(x1,y1),B(x2,y2)(x1
(2)若AB=
,求k的值.
(3)如图②,点P在函数y=(x>0)的图象上,点M在直线l2:y=-x+上,且PM∥x轴.若点N(0,2),求PM+PN的最小值,并求PM+PN取得最小值时点P的坐标.
教师样卷
1.
选择题(共15题;共30分)
1.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是(C)
A.
y3
y2
y1
y1
A.
1≤k≤4
B.
2≤k≤8
C.
2≤k≤16
D.
8≤k≤16
第2题图
第3题图
第5题图
3.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是(A)
A.
1
1≤x≤3
C.
x>1
D.
x<3
4.已知A(x1,y1),B(x2,y2)是反比例函数y=(k≠0)图象上的两个点,当x1<x2<0时,y1>y2,则一次函数y=kx-k的图象不经过(B)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
【解】 ∵当x1<x2<0时,y1>y2,∴k>0.∵一次函数y=kx-k的图象经过点(1,0)和点(0,-k),-k<0,∴一次函数的图象不经过第二象限
5.如图所示,已知点A是反比例函数y
=
(k
>
0)的图象上的一点,AB⊥y轴于点B,P是x轴上任意一点,若△ABP的面积为3,则k的值为(
C
)
A.3
B.
-
3
C.6
D.
-
6
6.已知y
=
y1+
y2,其中y与成反比例且比例系数为k1,y2与x成正比例且比例系数为k2.若x
=-
1时,y
=
0,则k1,k2的关系为(
A
)
A.k1
+
k2
=
0
B.k1k2
=
1
C.k1k2
=
-
1
D.k1
=
k2
7.已知点A在函数y1
=
-
(x
>
0)的图象上,点B在直线y2
=
kx
+
1
+
k(k为常数,且k≥0)上.若A,B两点关于原点对称,则陈点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为(
A
)
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
8.关于反比例函数,下列说法中错误的是( D )
A.当时,随的增大而增大
B.图象位于第二、四象限
C.点在函数图象上
D.当时,
【详解】∵<0,∴当时,随的增大而增大,故A不符合题意;∵,∴图象位于第二、四象限,故B不符合题意;当时,,故C不符合题意;当时,<2,故D错误,符合题意;故答案选D.
9.如图,反比例函数y=(k为常数,k≠0)的图象经过点A,过点A作AB⊥x轴,垂足为B.若△AOB的面积为2,则k的值为(
C
)
A.2
B.-2
C.4
D.-4
【详解】∵AB⊥x轴,垂足为B.若△AOB的面积为2,∴,∴k=4,∵反比例函数图象在第一象限,∴k=4,故选:C.
10.若点,在反比例函数的图象上,且,则的取值范围是(
B
)
A.
B.
C.
D.或
解:∵反比例函数,∴图象经过第二、四象限,在每个象限内,y随x的增大而增大,①若点A、点B同在第二或第四象限,∵,∴a>a+1,此不等式无解;②若点A在第二象限,且点B在第四象限,∵,∴,
解得:;③由y1>y2,可知点A在第四象限,且点B在第二象限这种情况不可能,综上,的取值范围是,故选:B.
11
若、都在函数y=的图象上,且,则(
A
)
B.
B.
C.
D.
解:函数y=,该函数图象在第一、三象限、在每个象限内y随x的增大而减小,∵、都在函数y=的图象上,且
,∴,故选A.
12.如图,在平面直角坐标系中,轴于点,,双曲线过点,交于点,连接,.若,,则的值为(
D
)
A.
B.
C.
D.
【详解】如图:过点A作AH垂直于x轴于点H,设,轴,四边形OCBH为矩形,OH=BC,CO=BH
AH=BH-AB=4a-3a=a,点A坐标(),,双曲线与BC交于点D,点D的坐标(),,,S矩形COHB,,,
,,
S矩形COHB,整理得:,解得:,故选:D.
13.下列图形中,阴影部分面积最大的是(
C
)
A.
B.
C.D.
【详解】A、根据反比例函数系数k的几何意义,阴影部分面积和为:xy=3.B、根据反比例函数系数k的几何意义,阴影部分面积和为:
|xy|=3
.C、如图,过点M作MA⊥x轴于点A,过点N作NB⊥x轴于点B,
根据反比例函数系数k的几何意义,S△OAM=S△OBM=
|xy|=
,从而阴影部分面积和为梯形MABN的面积:
(1+3)×2=4
.D、根据M,N点的坐标以及三角形面积求法得出,阴影部分面积为:×1×6=3
.综上所述,阴影部分面积最大的是C.故选:C.
14.如图,是反比例函数图象上第二象限内的一点,轴,垂足为,若的面积为,则的值为(
A
)
A.
B.
C.
D.
【详解】根据题意得:,解得k=4或k=-4,∵函数图象在第二象限内,∴k=-4,故选:A.
15.反比例函数的图象上有两点,,若,则下列结论正确的是(
D
)
A.
B.
C.
D.
解:∵,∴xy=-1.∴x、y异号.∵x1<0<x2,∴y1>0>y2.故选:D.
2.
填空题(共10题;共20分)
16.如图所示,反比例函数y
=
(k
<
0)的图象与经过原点的直线相交于A,B两点,已知点A的坐标为(
-
2,1),则点B的坐标为
_(2,-1)________
.
第16题图
第18题图
第19题图
第20题图
17.若A(
-
1,m)与B(2,m
-
3)是反比例函数y
=
图象上的两个点,则m
=
___2______
.
18.如图所示,A,C分别是正比例函数y
=
x的图象与反比例函数y
=
的图象的交点,过点A作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD的面积为
___8______
.
19.如图所示,正方形ABCD的顶点A,D分别在x轴、y轴上,∠ADO
=
30°,OA
=
2,反比例函数y
=
经过CD的中点M,那么k
=
__+6_______
.
20.如图所示,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y
=
(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF
=
2AF,则k的值为
___-6______
.
21.已知点A(1,m),B(2,n)在反比例函数y=-的图象上,则m与n的大小关系为__m<n__.
22.有下列函数:①y=-;②y=2x-1;③y=-x;④y=;⑤y=(x>0);⑥y=-(x<0).其中y随x的增大而增大的是__②⑥__(填序号).
23.如图,点A在反比例函数y=(x>0)的图象上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为__+1__.
第23题图
第24题图
第25题图
24.如图,矩形ABCD的顶点A,C都在反比例函数y=(k>0,x>0)的图象上.若顶点D的坐标为(5,3),则直线BD的函数表达式是__y=x__.
【解】 ∵点D(5,3),点A,C都在反比例函数y=的图象上,∴点A,C,
∴点B.设直线BD的函数表达式为y=mx+n.把点D(5,3),B的坐标代入,得
f(k,3)m+n=f(k,5),))解得
n=0.))∴直线BD的函数表达式为y=x.
25如图,已知在平面直角坐标系xOy中,直线y=x-1分别交x轴、y轴于点A和点B,分别交反比例函数y1=(k>0,x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD.若△COE的面积与△DOB的面积相等,则k的值为___2__.
【解】 设点C(x1,y1),D(x2,y2).∵直线y=x-1与y轴相交于点B,∴点B(0,-1),∴OB=1.∵点C在反比例函数y1=(k>0)的图象上,∴S△COE=x1·y1=k.又∵S△BOD=S△COE=k=|x2|×1,∴x2=-k.∵点D在反比例函数y=(k>0)的图象上,∴点D(-k,-2).∵点D(-k,-2)在直线y=x-1上,∴×(-k)-1=-2,解得k=2.
3.
解答题(共9小题
共70分)
26.
(6分)作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2<y<3时,求x的取值范围;
(3)当-3<x<2时,求y的取值范围.
解:作图略(1)y=-6 (2)4<x<6 (3)y<-4或y>6
27.(6分)如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)在图象上取一点P,分别作x轴、y轴的垂线,垂足分别为点Q,R,四边形PQOR的面积为3,求n的值.
解:(1)图象的另一支位于第四象限,n<-3 (2)n=-6
28.
(6分)如图,一次函数y=-x+2的图象与x轴交于点B,与反比例函数y=的图象的交点为A(-2,3).
(1)求反比例函数的表达式;
(2)过点A作AC⊥x轴,垂足为点C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.
解:(1)反比例函数的表达式为y=- (2)设点P的坐标是(a,b).∵一次函数y=-x+2的图象与x轴交于点B,∴当y=0时,-x+2=0,解得x=4,∴点B的坐标是(4,0),即OB=4.∴BC=6.∵△PBC的面积等于18,∴×BC×|b|=18,解得|b|=6,∴b1=6,b2=-6,∴点P的坐标是(-1,6),(1,-6)
29.
(6分)已知反比例函数y=的图象与一次函数y=3x+m的图象相交于点(1,5).
(1)
求这两个函数的解析式;
(2)
求这两个函数图象的另一个交点的坐标.
解:(1)
把x=1,y=5分别代入,得k=5,m=2,∴解析式分别为y=和y=3x+2.
(2)
解方程组eq
blc{(avs4alco1(y=,
y=3x+2)),得,
eq
blc{(avs4alco1(x2=-,y2=-3)).∴另一个交点的坐标为(-,-3).
30.(6分)如图,已知双曲线y=
(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,求k的值.
解:设F(a,b),∵F在y=上,∴ab=k.∵F为AB的中点,∴B(a,2b),E(a,2b).∵S四边形OEBF=S矩形OABC
–
S△OCE
–
S△OAF∴2=a·2b-×a·2b-
a·b,即k=ab=2。
31
(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)若P是y轴一点,且满足△PAB的面积是5,求P点坐标.
解:(1)一次函数表达式为y=x+1,反比例函数表达式为y= (2)设P点坐标为(0,b),设直线y=x+1与y轴的交点为C,则C点坐标为(0,1),∴PC=|b-1|,∵S△PAC+S△PBC=S△PAB,∴|b-1|×2+|b-1|×3=5,∴|b-1|=2,∴b=3或-1,∴P点坐标为(0,3)或(0,-1)
32.
(8分)如图,一次函数y=k1x+b(k1≠0)与反比例函数y=(k2≠0)的图象交于点A(-1,2),B(m,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
解:(1)把A(-1,2)代入y=,得到k2=-2,∴反比例函数的表达式为y=-.∵B(m,-1)在y=-上,∴m=2,由题意,解得,∴一次函数的表达式为y=-x+1
(2)∵A(-1,2),B(2,-1),∴AB=3,①当PA=PB时,(n+1)2+4=(n-2)2+1,∴n=0,∵n>0,∴n=0不合题意舍弃.②当AP=AB时,22+(n+1)2=(3)2,∵n>0,∴n=-1+.③当BP=BA时,12+(n-2)2=(3)2,∵n>0,∴n=2+.综上所述,n=-1+或2+
33.(8分)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.
(1)求反比例函数的表达式.
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,则点P,Q各位于哪个象限?并简要说明理由.
【解】 (1)由题意得,点B,把点B的坐标代入y=中,得=-,解得k=-3,∴反比例函数的表达式为y=-.
(2)点P在第二象限,点Q在第四象限.理由如下:∵k=-3<0,∴反比例函数y=-在每个象限内,y随x的增大而增大.∵P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,∴点P在第二象限,点Q在第四象限.
34.(12分)如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)的图象相交于第一、三象限内的A(3,5),B(a,-3)两点,与x轴相交于点C.
(1)求一次函数和反比例函数的表达式.
(2)在y轴上找一点P,使PB-PC最大,求PB-PC的最大值及点P的坐标[参考公式:在平面直角坐标系中,若点A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=].
(3)直接写出当y1>y2时,x的取值范围.
【解】 (1)把点A(3,5)的坐标代入y2=(m≠0),得m=3×5=15,∴反比例函数的表达式为y2=.把点B(a,-3)的坐标代入y2=,得a=-5,∴点B(-5,-3).把点A(3,5),B(-5,-3)的坐标代入y=kx+b,得
-5k+b=-3,))解得
b=2.))∴一次函数的表达式为y1=x+2.
(2)在y轴上任取一点M,连结MB,MC,则MB-MC≤BC,当且仅当点M在直线BC上时取等号,∴点P为一次函数y1=x+2的图象与y轴的交点坐标.
令x=0,则y=x+2=2,∴点P(0,2).令y=x+2=0,则x=-2,∴点C(-2,0),
∴BC==3,即PB-PC的最大值为3.
(3)当y1>y2时,-5<x<0或x>3.
35.(12分)如图①,直线l1:y-=k(x-)(k<0)过定点F,且与反比例函数y=(x>0)的图象相交于A,B两点.设点A(x1,y1),B(x2,y2)(x1
(2)若AB=
,求k的值.
(3)如图②,点P在函数y=(x>0)的图象上,点M在直线l2:y=-x+上,且PM∥x轴.若点N(0,2),求PM+PN的最小值,并求PM+PN取得最小值时点P的坐标.
【解】 (1)当k=-1时,直线l1:y-=-(x-),即y=-x+2.
联立解得
如解图①,设直线l1与y轴相交于点C,则点C(0,2).∴S=S△BOC-S△AOC=×2×(x2-x1)=×2×2=2.
,
(2)联立整理,得kx2+(1-k)x-1=0(k<0).∵Δ=[(1-k)]2+4k=2(1+k2)>0,∴x1,x2是方程kx2+(1-k)x-1=0(k<0)的两个根,∴∴AB==
=·=·=·=·=-.
∵AB=
,∴-=
,整理,得2k2+5k+2=0,解得k1=-2,k2=-.
(3)∵直线l1:y-=k(x-)(k<0)过定点F,∴点F(,).如解图②,设点P,则点M(-+,),∴PM=x+-.设m=x+,则PM=m-(m>).
∵PF======m-,∴PM=PF,∴PM+PN=PF+PN≥NF,∴当点P在NF上时,PM+PN取得最小值.∵点N(0,2),F(,),∴NF==2,∴PM+PN的最小值是2.由(1)易知此时点P(-1,+1).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
