第18章 平行四边形-2020-2021学年八年级数学下册疑难易错题汇编(含解析)
文档属性
| 名称 | 第18章 平行四边形-2020-2021学年八年级数学下册疑难易错题汇编(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 平行四边形 疑难易错题汇编
一、选择题(共14小题,每题只有一个选项符合题意)
1.(2020?广州)△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=( )
A.22° B.68° C.96° D.112°
2.(2020?眉山)下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
3.(2019?玉林)_???????????¨??????_ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中矩形的个数共有( )【来源:21·世纪·教育·网】
A.5个 B.8个 C.9个 D.11个
4.(2020?黄石_??????????????¨R_t△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为( )www-2-1-cnjy-com
A.3 B.4 C.5 D.6
5.(2019?威海)_?????????E?????±_ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )【出处:21教育名师】
A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
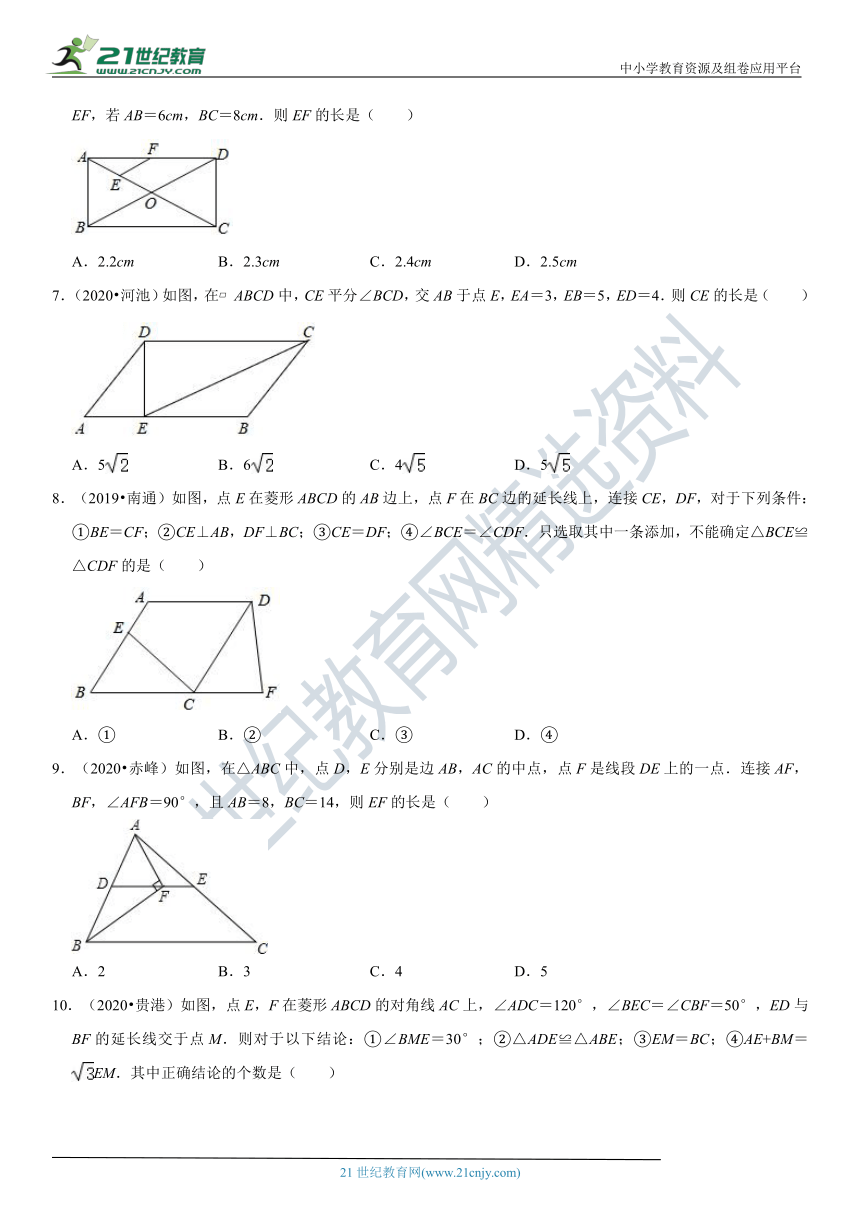
6.(2019_???????±??????????_,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
7.(2020?河池)如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
8.(2019?南_é?????????????????_E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是( )
A.① B.② C.③ D.④
9.(2020?赤峰)如图,在△_ABC?????????_D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A.2 B.3 C.4 D.5
10.(2020?贵港)如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
11.(2020?绵阳)如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
12.(2020?锦州)_???????????¨è?±???_ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
13.(20_20???????¤????_如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
A.13 B.10 C.12 D.5
14.(20_20???é???°??¤?_斯)如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3,连接A1A3,得到△A1A2A3,再以对角线OA3为边作第四个正方形OA3A4B4,连接A2A4,得到△A2A3A4,…,设△AA1A2,△A1A2A3,△A2A3A4,…,的面积分别为S1,S2,S3,…,如此下去,则S2020的值为( )
A. B.22018 C.22018+ D.1010
二.填空题(共6小题)
15.(2020?广安)已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为 cm.
16.(2020?金华)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
17.(2020?鸡西)_???????????¨???è??_形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形(填一个即可).
18.(2020?大连)如图,菱形ABCD中,∠ACD=40°,则∠ABC= °.
19.(2020?德阳)如_????????¨???è?????_边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF= .
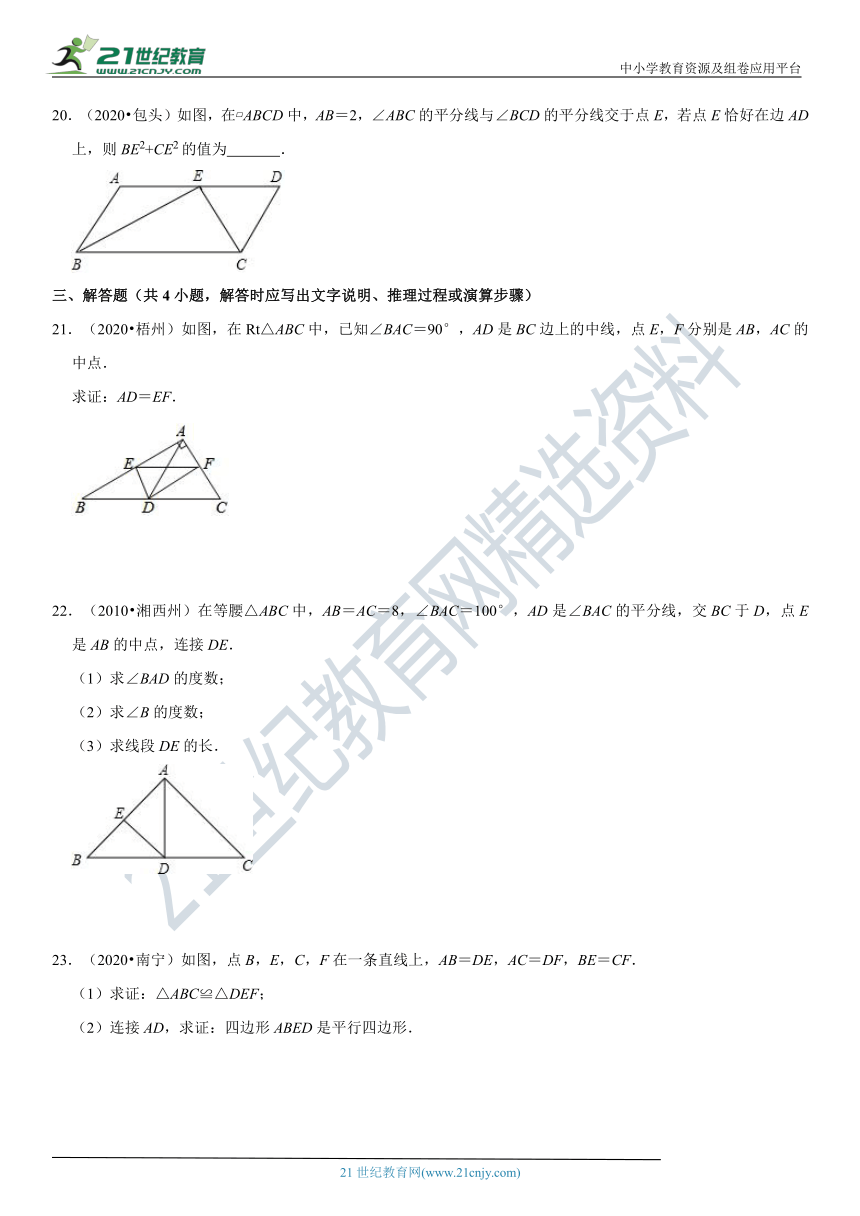
20.(2020?包头)如图_?????¨??±ABC_D中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
三、解答题(共4小题,解答时应写出文字说明、推理过程或演算步骤)
21.(2020?梧州)如图,在Rt△ABC中,已知∠BAC=90°,AD是BC边上的中线,点E,F分别是AB,AC的中点.
求证:AD=EF.
22.(2010?湘西州)_??¨???è?°???AB_C中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.
(1)求∠BAD的度数;
(2)求∠B的度数;
(3)求线段DE的长.
23.(2020?南宁)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
24.(2020?鄂州)如图,在_???è?????è?????A_BCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.21世纪教育网版权所有
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
第18章 平行四边形 疑难易错题汇编
一、选择题(共14小题,每题只有一个选项符合题意)
1.(2020?广州)△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=( )
A.22° B.68° C.96° D.112°
解:∵点D、E分别是△ABC的边AB、AC的中点,
∴DE∥BC,
∴∠AED=∠C,
∵∠C=68°,
∴∠AED=∠C=68°.
答案:B.
2.(2020?眉山)下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
解:A、一组对边平行另一组对边相等的四边形可以是等腰梯形,可以是平行四边形,故选项A不合题意;
B、对角线互相垂直平分的四边形是菱形,故选项B符合题意;
C、对角线相等的平行四边形是矩形,故选项C不合题意;
D、对角线互相垂直平分且相等的四边形是正方形,故选项D不合题意;
答案:B.
3.(2019?玉_?????????????????¨_矩形ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中矩形的个数共有( )2·1·c·n·j·y
A.5个 B.8个 C.9个 D.11个
解:∵E,G分别是边DA,BC的中点,四边形ABCD是矩形,
∴四边形DEGC、AEGB是矩形,
同理四边形ADHF、BCHF是矩形,
则图中四个小四边形是矩形,
故图中矩形的个数共有9个,
答案:C.
4.(2020?黄石)_???????????¨Rt_△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为( )21教育名师原创作品
A.3 B.4 C.5 D.6
解:∵在Rt△ABC中,∠ACB=90°,点H,E,F分别是边AB,BC,CA的中点,
∴EF=AB,CH=AB,
∴EF=CH,
∵EF+CH=8,
∴CH=EF=8=4,
答案:B.
5.(2019?_?¨???·????????????_E是?ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴BCED为平行四边形,故A正确;
∵DE∥BC,
∴∠DEF=∠CBF,
在△DEF与△CBF中,,
∴△DEF≌△CBF(AAS),
∴EF=BF,
∵DF=CF,
∴四边形BCED为平行四边形,故B正确;
∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故C错误;
∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确,
答案:C.
6.如图,在矩形ABCD中,对角_???AC???BD_相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )21*cnjy*com
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=6cm,BC=8cm,
∴由勾股定理得:AC===10(cm),
∴BD=10cm,DO=5cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=OD=2.5cm,
答案:D.
7.(2020?河池)如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
解:∵CE平分∠BCD,
∴∠BCE=∠DCE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠BCE,
∴BC=BE=5,
∴AD=5,
∵EA=3,ED=4,
在△AED中,32+42=52,即EA2+ED2=AD2,
∴∠AED=90°,
∴CD=AB=3+5=8,∠EDC=90°,
在Rt△EDC中,CE===4.
答案:C.
8.如图,点E在菱形ABCD的_ABè???????????_F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是( )21·cn·jy·com
A.① B.② C.③ D.④
解:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,
∴∠B=∠DCF,
①∵添加BE=CF,
∴△BCE≌△CDF(SAS),
②∵添加CE⊥AB,DF⊥BC,
∴∠CEB=∠F=90°,
∴△BCE≌△CDF(AAS),
③∵添加CE=DF,
不能确定△BCE≌△CDF;
④∵添加∠BCE=∠CDF,
∴△BCE≌△CDF(ASA),
答案:C.
9.(2020?赤峰)如图,在△_ABC?????????_D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )21·世纪*教育网
A.2 B.3 C.4 D.5
解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=BC=7,
∵∠AFB=90°,AB=8,
∴DF=AB=4,
∴EF=DE﹣DF=7﹣4=3,
答案:B.
10.(2020?贵港)如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是( )【来源:21cnj*y.co*m】
A.1个 B.2个 C.3个 D.4个
解:∵四边形ABD是菱形,∠ADC=120°,
∴AD=AB=BC=CD,∠BAD=∠BCD=60°,∠DAE=∠BAE,∠DCE=∠BCE=∠BCD=30°,
∵∠BFE=∠BCE+∠CBF=30°+50°=80°,
∴∠EBF=180°﹣∠BEC﹣∠BFE=180°﹣50°﹣80°=50°,
在△CDE和△CBE中,
,
∴△CDE≌△CBE(SAS),
∴∠DEC=∠BEC=50°,
∴∠BEM=∠DEC+∠BEC=100°,
∴∠BME=180°﹣∠BEM﹣∠EBF=180°﹣100°﹣50°=30°,故①正确;
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),故②正确;
∵∠EBC=∠EBF+∠CBF=100°,
∴∠BEM=∠EBC,
在△BEM和△EBC中,
,
∴△BEM≌△EBC(AAS),
∴BM=EC,EM=BC,故③正确;
连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,AC⊥BD,
∵∠DCO=30°,
∴OD=CD=BC,OC=OD,
∴OC=BC,
∴AC=2OC=BC,
∵BM=EC,EM=BC,
∴AE+BM=AE+EC=AC=BC=EM,故④正确,
正确结论的个数是4个,
答案:D.
11.(2020?绵阳)如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
所以此图形的对称轴有4条.
答案:B.
12.(2020?_é???·?????????????_在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )21*cnjy*com
A.4 B. C.6 D.
解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
答案:B.
13.(2020?宁夏)如图,菱_???ABCD???_边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )21教育网
A.13 B.10 C.12 D.5
解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=13,EF∥BD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=13,CO=12,
∴OB=OD==5,
∴BD=2OD=10,
∴EG=BD=10;
答案:B.
14.(202_0???é???°??¤????_)如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3,连接A1A3,得到△A1A2A3,再以对角线OA3为边作第四个正方形OA3A4B4,连接A2A4,得到△A2A3A4,…,设△AA1A2,△A1A2A3,△A2A3A4,…,的面积分别为S1,S2,S3,…,如此下去,则S2020的值为( )2-1-c-n-j-y
A. B.22018 C.22018+ D.1010
解:∵四边形OAA1B1是正方形,
∴OA=AA1=A1B1=1,
∴S1=1×1=,
∵∠OAA1=90°,
∴OA12=12+12=2,
∴OA2=A2A3=2,
∴S2=2×1=1,
同理可求:S3=2×2=2,S4=4…,
∴Sn=2n﹣2,
∴S2020=22018,
答案:B.
二.填空题(共6小题)
15.(2020?广安)已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为 17 cm.21cnjy.com
解:∵D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC=3.5(cm),
同理,EF=AB=6(cm),DE=AC=7.5(cm),
∴△DEF的周长=3.5+6+7.5=17(cm),
故答案为:17.
16.(2020?金华)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 30 °.
解:∵四边形ABCD是平行四边形,
∴∠D+∠C=180°,
∴∠α=180°﹣(540°﹣70°﹣140°﹣180°)=30°,
故答案为:30.
17.(202_0???é??è????????_图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 AB∥CD(答案不唯一) ,使四边形ABCD是平行四边形(填一个即可).【版权所有:21教育】
解:根据平行四边形的判定,可再添加一个条件:AB∥CD.
故答案为:AB∥CD(答案不唯一).
18.(2020?大连)如图,菱形ABCD中,∠ACD=40°,则∠ABC= 100 °.
解:∵四边形ABCD是菱形,
∴AB∥CD,∠BCD=2∠ACD=80°,
∴∠ABC+∠BCD=180°,
∴∠ABC=180°﹣80°=100°;
故答案为:100.
19.(2020?德阳)_???????????¨???è??_四边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF= 2 .
解:在平行四边形ABCD中,AB∥CD,
∴∠ABE=∠BEC.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠BEC,
∴CB=CE.
∵CF⊥BE,
∴BF=EF.
∵G是AB的中点,
∴GF是△ABE的中位线,
∴GF=AE,
∵AE=4,
∴GF=2.
故答案为2.
20.(2020?包头)如图_?????¨??±ABC_D中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 16 .
解:∵BE、CE 分别平分∠ABC 和∠BCD
∴∠EBC=∠ABC,∠ECB=∠BCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,BC=AD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴BE2+CE2=BC2 ,
∵AD∥BC,
∴∠EBC=∠AEB,
∵BE平分∠ABC,
∴∠EBC=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=2,
同理可证 DE=DC=2,
∴DE+AE=AD=4,
∴BE2+CE2=BC2=AD2=16.
故答案为:16.
三、解答题(共4小题,解答时应写出文字说明、推理过程或演算步骤)
21.(2020?梧州)如图,在Rt△ABC中,已知∠BAC=90°,AD是BC边上的中线,点E,F分别是AB,AC的中点.www.21-cn-jy.com
求证:AD=EF.
证明:在Rt△ABC中,AD是BC边上的中线,
∴AD=BC,
∵点E,F分别是AB,AC的中点,
∴EF是△ABC的中位线,
∴EF=BC,
∴AD=EF.
22.(2010?湘西_?·??????¨???è?°???_ABC中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.
(1)求∠BAD的度数;
(2)求∠B的度数;
(3)求线段DE的长.
解:(1)∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠BAC=100°,
∴∠BAD=50°;
(2)∵AB=AC,
∴∠B=∠C,
∴∠;
(3)∵AB=AC,AD平分∠BAC,
∴AD是等腰△ABC底边BC上的高,即∠ADB=90°
在直角三角形ABD中,点E是AB的中点,
∴DE为斜边AB边上的中线,
∴DE=.
23.(2020?南宁)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS);
(2)证明:由(1)得:△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE,
又∵AB=DE,
∴四边形ABED是平行四边形.
24.(2020?鄂州_??????????????¨???_行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
_21?????????è?????(www.21cnjy.com)_
第18章 平行四边形 疑难易错题汇编
一、选择题(共14小题,每题只有一个选项符合题意)
1.(2020?广州)△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=( )
A.22° B.68° C.96° D.112°
2.(2020?眉山)下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
3.(2019?玉林)_???????????¨??????_ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中矩形的个数共有( )【来源:21·世纪·教育·网】
A.5个 B.8个 C.9个 D.11个
4.(2020?黄石_??????????????¨R_t△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为( )www-2-1-cnjy-com
A.3 B.4 C.5 D.6
5.(2019?威海)_?????????E?????±_ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )【出处:21教育名师】
A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
6.(2019_???????±??????????_,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
7.(2020?河池)如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
8.(2019?南_é?????????????????_E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是( )
A.① B.② C.③ D.④
9.(2020?赤峰)如图,在△_ABC?????????_D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A.2 B.3 C.4 D.5
10.(2020?贵港)如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
11.(2020?绵阳)如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
12.(2020?锦州)_???????????¨è?±???_ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
13.(20_20???????¤????_如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
A.13 B.10 C.12 D.5
14.(20_20???é???°??¤?_斯)如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3,连接A1A3,得到△A1A2A3,再以对角线OA3为边作第四个正方形OA3A4B4,连接A2A4,得到△A2A3A4,…,设△AA1A2,△A1A2A3,△A2A3A4,…,的面积分别为S1,S2,S3,…,如此下去,则S2020的值为( )
A. B.22018 C.22018+ D.1010
二.填空题(共6小题)
15.(2020?广安)已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为 cm.
16.(2020?金华)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
17.(2020?鸡西)_???????????¨???è??_形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形(填一个即可).
18.(2020?大连)如图,菱形ABCD中,∠ACD=40°,则∠ABC= °.
19.(2020?德阳)如_????????¨???è?????_边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF= .
20.(2020?包头)如图_?????¨??±ABC_D中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
三、解答题(共4小题,解答时应写出文字说明、推理过程或演算步骤)
21.(2020?梧州)如图,在Rt△ABC中,已知∠BAC=90°,AD是BC边上的中线,点E,F分别是AB,AC的中点.
求证:AD=EF.
22.(2010?湘西州)_??¨???è?°???AB_C中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.
(1)求∠BAD的度数;
(2)求∠B的度数;
(3)求线段DE的长.
23.(2020?南宁)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
24.(2020?鄂州)如图,在_???è?????è?????A_BCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.21世纪教育网版权所有
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
第18章 平行四边形 疑难易错题汇编
一、选择题(共14小题,每题只有一个选项符合题意)
1.(2020?广州)△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=( )
A.22° B.68° C.96° D.112°
解:∵点D、E分别是△ABC的边AB、AC的中点,
∴DE∥BC,
∴∠AED=∠C,
∵∠C=68°,
∴∠AED=∠C=68°.
答案:B.
2.(2020?眉山)下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
解:A、一组对边平行另一组对边相等的四边形可以是等腰梯形,可以是平行四边形,故选项A不合题意;
B、对角线互相垂直平分的四边形是菱形,故选项B符合题意;
C、对角线相等的平行四边形是矩形,故选项C不合题意;
D、对角线互相垂直平分且相等的四边形是正方形,故选项D不合题意;
答案:B.
3.(2019?玉_?????????????????¨_矩形ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中矩形的个数共有( )2·1·c·n·j·y
A.5个 B.8个 C.9个 D.11个
解:∵E,G分别是边DA,BC的中点,四边形ABCD是矩形,
∴四边形DEGC、AEGB是矩形,
同理四边形ADHF、BCHF是矩形,
则图中四个小四边形是矩形,
故图中矩形的个数共有9个,
答案:C.
4.(2020?黄石)_???????????¨Rt_△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为( )21教育名师原创作品
A.3 B.4 C.5 D.6
解:∵在Rt△ABC中,∠ACB=90°,点H,E,F分别是边AB,BC,CA的中点,
∴EF=AB,CH=AB,
∴EF=CH,
∵EF+CH=8,
∴CH=EF=8=4,
答案:B.
5.(2019?_?¨???·????????????_E是?ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴BCED为平行四边形,故A正确;
∵DE∥BC,
∴∠DEF=∠CBF,
在△DEF与△CBF中,,
∴△DEF≌△CBF(AAS),
∴EF=BF,
∵DF=CF,
∴四边形BCED为平行四边形,故B正确;
∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故C错误;
∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确,
答案:C.
6.如图,在矩形ABCD中,对角_???AC???BD_相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )21*cnjy*com
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=6cm,BC=8cm,
∴由勾股定理得:AC===10(cm),
∴BD=10cm,DO=5cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=OD=2.5cm,
答案:D.
7.(2020?河池)如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
解:∵CE平分∠BCD,
∴∠BCE=∠DCE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠BCE,
∴BC=BE=5,
∴AD=5,
∵EA=3,ED=4,
在△AED中,32+42=52,即EA2+ED2=AD2,
∴∠AED=90°,
∴CD=AB=3+5=8,∠EDC=90°,
在Rt△EDC中,CE===4.
答案:C.
8.如图,点E在菱形ABCD的_ABè???????????_F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是( )21·cn·jy·com
A.① B.② C.③ D.④
解:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,
∴∠B=∠DCF,
①∵添加BE=CF,
∴△BCE≌△CDF(SAS),
②∵添加CE⊥AB,DF⊥BC,
∴∠CEB=∠F=90°,
∴△BCE≌△CDF(AAS),
③∵添加CE=DF,
不能确定△BCE≌△CDF;
④∵添加∠BCE=∠CDF,
∴△BCE≌△CDF(ASA),
答案:C.
9.(2020?赤峰)如图,在△_ABC?????????_D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )21·世纪*教育网
A.2 B.3 C.4 D.5
解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=BC=7,
∵∠AFB=90°,AB=8,
∴DF=AB=4,
∴EF=DE﹣DF=7﹣4=3,
答案:B.
10.(2020?贵港)如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是( )【来源:21cnj*y.co*m】
A.1个 B.2个 C.3个 D.4个
解:∵四边形ABD是菱形,∠ADC=120°,
∴AD=AB=BC=CD,∠BAD=∠BCD=60°,∠DAE=∠BAE,∠DCE=∠BCE=∠BCD=30°,
∵∠BFE=∠BCE+∠CBF=30°+50°=80°,
∴∠EBF=180°﹣∠BEC﹣∠BFE=180°﹣50°﹣80°=50°,
在△CDE和△CBE中,
,
∴△CDE≌△CBE(SAS),
∴∠DEC=∠BEC=50°,
∴∠BEM=∠DEC+∠BEC=100°,
∴∠BME=180°﹣∠BEM﹣∠EBF=180°﹣100°﹣50°=30°,故①正确;
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),故②正确;
∵∠EBC=∠EBF+∠CBF=100°,
∴∠BEM=∠EBC,
在△BEM和△EBC中,
,
∴△BEM≌△EBC(AAS),
∴BM=EC,EM=BC,故③正确;
连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,AC⊥BD,
∵∠DCO=30°,
∴OD=CD=BC,OC=OD,
∴OC=BC,
∴AC=2OC=BC,
∵BM=EC,EM=BC,
∴AE+BM=AE+EC=AC=BC=EM,故④正确,
正确结论的个数是4个,
答案:D.
11.(2020?绵阳)如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
所以此图形的对称轴有4条.
答案:B.
12.(2020?_é???·?????????????_在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )21*cnjy*com
A.4 B. C.6 D.
解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
答案:B.
13.(2020?宁夏)如图,菱_???ABCD???_边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )21教育网
A.13 B.10 C.12 D.5
解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=13,EF∥BD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=13,CO=12,
∴OB=OD==5,
∴BD=2OD=10,
∴EG=BD=10;
答案:B.
14.(202_0???é???°??¤????_)如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3,连接A1A3,得到△A1A2A3,再以对角线OA3为边作第四个正方形OA3A4B4,连接A2A4,得到△A2A3A4,…,设△AA1A2,△A1A2A3,△A2A3A4,…,的面积分别为S1,S2,S3,…,如此下去,则S2020的值为( )2-1-c-n-j-y
A. B.22018 C.22018+ D.1010
解:∵四边形OAA1B1是正方形,
∴OA=AA1=A1B1=1,
∴S1=1×1=,
∵∠OAA1=90°,
∴OA12=12+12=2,
∴OA2=A2A3=2,
∴S2=2×1=1,
同理可求:S3=2×2=2,S4=4…,
∴Sn=2n﹣2,
∴S2020=22018,
答案:B.
二.填空题(共6小题)
15.(2020?广安)已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为 17 cm.21cnjy.com
解:∵D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC=3.5(cm),
同理,EF=AB=6(cm),DE=AC=7.5(cm),
∴△DEF的周长=3.5+6+7.5=17(cm),
故答案为:17.
16.(2020?金华)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 30 °.
解:∵四边形ABCD是平行四边形,
∴∠D+∠C=180°,
∴∠α=180°﹣(540°﹣70°﹣140°﹣180°)=30°,
故答案为:30.
17.(202_0???é??è????????_图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 AB∥CD(答案不唯一) ,使四边形ABCD是平行四边形(填一个即可).【版权所有:21教育】
解:根据平行四边形的判定,可再添加一个条件:AB∥CD.
故答案为:AB∥CD(答案不唯一).
18.(2020?大连)如图,菱形ABCD中,∠ACD=40°,则∠ABC= 100 °.
解:∵四边形ABCD是菱形,
∴AB∥CD,∠BCD=2∠ACD=80°,
∴∠ABC+∠BCD=180°,
∴∠ABC=180°﹣80°=100°;
故答案为:100.
19.(2020?德阳)_???????????¨???è??_四边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF= 2 .
解:在平行四边形ABCD中,AB∥CD,
∴∠ABE=∠BEC.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CBE=∠BEC,
∴CB=CE.
∵CF⊥BE,
∴BF=EF.
∵G是AB的中点,
∴GF是△ABE的中位线,
∴GF=AE,
∵AE=4,
∴GF=2.
故答案为2.
20.(2020?包头)如图_?????¨??±ABC_D中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 16 .
解:∵BE、CE 分别平分∠ABC 和∠BCD
∴∠EBC=∠ABC,∠ECB=∠BCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,BC=AD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴BE2+CE2=BC2 ,
∵AD∥BC,
∴∠EBC=∠AEB,
∵BE平分∠ABC,
∴∠EBC=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=2,
同理可证 DE=DC=2,
∴DE+AE=AD=4,
∴BE2+CE2=BC2=AD2=16.
故答案为:16.
三、解答题(共4小题,解答时应写出文字说明、推理过程或演算步骤)
21.(2020?梧州)如图,在Rt△ABC中,已知∠BAC=90°,AD是BC边上的中线,点E,F分别是AB,AC的中点.www.21-cn-jy.com
求证:AD=EF.
证明:在Rt△ABC中,AD是BC边上的中线,
∴AD=BC,
∵点E,F分别是AB,AC的中点,
∴EF是△ABC的中位线,
∴EF=BC,
∴AD=EF.
22.(2010?湘西_?·??????¨???è?°???_ABC中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.
(1)求∠BAD的度数;
(2)求∠B的度数;
(3)求线段DE的长.
解:(1)∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠BAC=100°,
∴∠BAD=50°;
(2)∵AB=AC,
∴∠B=∠C,
∴∠;
(3)∵AB=AC,AD平分∠BAC,
∴AD是等腰△ABC底边BC上的高,即∠ADB=90°
在直角三角形ABD中,点E是AB的中点,
∴DE为斜边AB边上的中线,
∴DE=.
23.(2020?南宁)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS);
(2)证明:由(1)得:△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE,
又∵AB=DE,
∴四边形ABED是平行四边形.
24.(2020?鄂州_??????????????¨???_行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
_21?????????è?????(www.21cnjy.com)_
