2020--2021学年北师大版八年级数学下册3.3 :中心对称(共21张ppt)
文档属性
| 名称 | 2020--2021学年北师大版八年级数学下册3.3 :中心对称(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 389.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 07:19:07 | ||
图片预览







文档简介
(共21张PPT)
第三章
图形的平移与旋转
3.3
中心对称
目标引领
1.理解中心对称的定义及性质,会识别中心对称图形。
2.会根据中心对称的性质画出与已知图形成中心对称的图形。
3.会运用掌握中心对称及中心对称图形的性质解决实际问题。(重点)
自主学习一
阅读课本本课时做一做之前的内容,思考下列问题:
1.中心对称的定义和对称中心的概念是什么?
2.你能画出图3-18和图3-19的对称中心,并用字母表示吗?
3.你认为中心对称的定义中需要重点关注的是哪几点?
如果把一个图形(如△ABO)绕定点O旋转180?,它能够与另一个图形(如△CDO)重合,那么就说这两个图形△ABO与图形△CDO关于点O的对称或中心对称,点O就是对称中心。
如图,△OCD
与△OAB
关于点O
中心对称
,则
是对称中心,点A与
是对称点,
点B与
是对称点。
概念展示:
O
B
C
A
D
O
C
D
归纳总结:
1.中心对称是一种特殊的旋转,其旋转角是180
°。
2.中心对称是对两个图形而言的,表示两个图形之间关系。
3.中心对称只有一个对称中心。
自主学习二
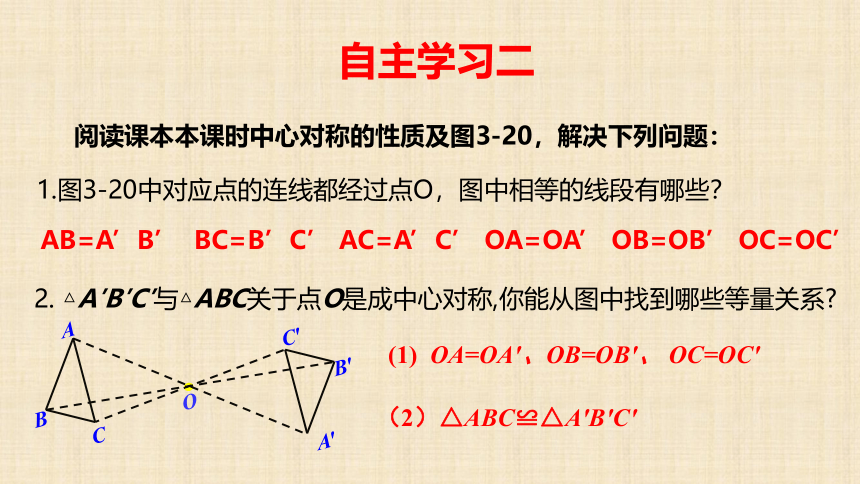
阅读课本本课时中心对称的性质及图3-20,解决下列问题:
1.图3-20中对应点的连线都经过点O,图中相等的线段有哪些?
AB=A’B’
BC=B’C’
AC=A’C’
OA=OA’
OB=OB’
OC=OC’
2.
△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系?
A′
B′
C′
A
B
C
O
(1)
OA=OA′、OB=OB′、
OC=OC′
(2)△ABC≌△A′B′C′
归纳总结:
1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分。
2.成中心对称的两个图形是全等图形,对应角相等,对应线段平行(或在同一直线上)且相等。
自主训练
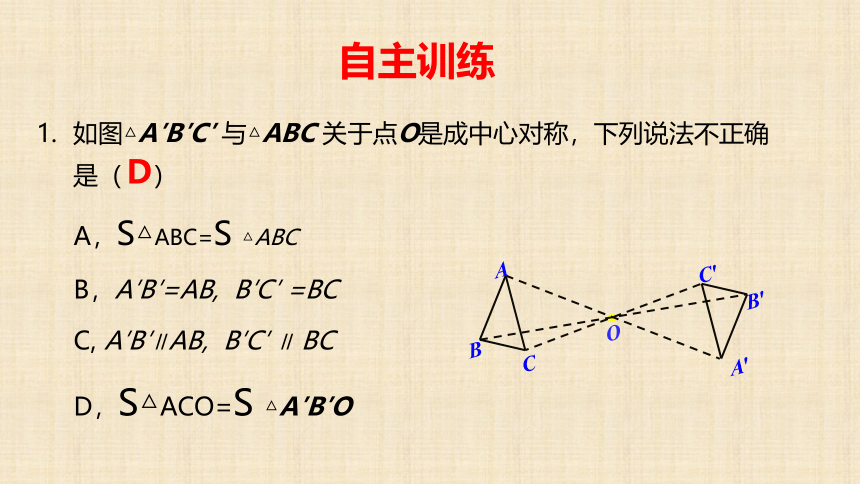
如图△A′B′C′
与△ABC
关于点O是成中心对称,下列说法不正确是(
)
A,S△ABC=S
△ABC
B,A′B′=AB,
B′C′
=BC
C,
A′B′∥AB,
B′C′
∥
BC
D,S△ACO=S
△A′B′O
A′
B′
C′
A
B
C
O
D
自主学习三
阅读课本本课时例题和议一仪中的内容,解决下列问题:
1.教材例题中的画图依据是什么?中心对称图形的定义是什么?
成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分。
2.
仿照例题中的方法,画出四边形ABCD关于O点的对称图形。
A
B
C
D
O
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对称点,再顺次连接各对应点即可。
把一个图形绕某个点旋转180?,如果旋转后图形能与原来图形重合,那么这个图形叫做中心对称图形,这个点叫做他的对称中心。
做法展示:
A
B
C
D
O
1.连接AO并延长到A',使OA'=OA,得到点A的对应点A';
A'
B'
C'
D'
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
合作交流:
根据中心对称的性质画已知图形关于某点成中心对称的图形的步骤是什么?
1.确定关键点:将各关键点(如多边形的各顶点)和对称中心连接并延长。
2.确定对应点:在延长线上取各关键点的对应点,使对应点到对称中心的
距离和关键点到对称中心的距离相等。
3.连线:按照原图将各对应点顺次连接即可得到所要画的图形。
自主训练
1,如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O。
A
B
C
A′
B′
C′
解法示范:
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O
即为所求(如图)。
A
B
C
A′
B′
C′
O
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图)。
O
A
B
C
A′
B′
C′
如果限制只用尺规作图,我们选方法二。
课时测评
√
√
(1)
(2)
(3)
√
(4)
1,下列图形中哪些是中心对称图形?
×
课时测评
2.如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高为________.
解析:设AB边上的高为h,因为△AOB的面积是12,AB=3,易得h=8.
又因为△AOB与△DOC成中心对称,△COD≌△AOB,所以△DOC中CD边上的高是8.
8
课时测评
3.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3。
3
轴
对
称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
当堂练习
1.判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.(
)
(2)成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形.
(
)
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形.
(
)
√
√
×
当堂练习
2.下列图形中是中心对称图形而不是轴对称图形的是
(
)
A
.
平行四边形
B.
矩形
C
.
菱形
D
.
正方形
A
A′
B′
C′
O
A
B
C
3.如图,已知等边三角形ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
总结归纳
中心对称和
中心对称图形
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
课后作业
1.完成本课时对应的课后习题。
2.完成本课时对应的导学测评和基础训练相关练习。
第三章
图形的平移与旋转
3.3
中心对称
目标引领
1.理解中心对称的定义及性质,会识别中心对称图形。
2.会根据中心对称的性质画出与已知图形成中心对称的图形。
3.会运用掌握中心对称及中心对称图形的性质解决实际问题。(重点)
自主学习一
阅读课本本课时做一做之前的内容,思考下列问题:
1.中心对称的定义和对称中心的概念是什么?
2.你能画出图3-18和图3-19的对称中心,并用字母表示吗?
3.你认为中心对称的定义中需要重点关注的是哪几点?
如果把一个图形(如△ABO)绕定点O旋转180?,它能够与另一个图形(如△CDO)重合,那么就说这两个图形△ABO与图形△CDO关于点O的对称或中心对称,点O就是对称中心。
如图,△OCD
与△OAB
关于点O
中心对称
,则
是对称中心,点A与
是对称点,
点B与
是对称点。
概念展示:
O
B
C
A
D
O
C
D
归纳总结:
1.中心对称是一种特殊的旋转,其旋转角是180
°。
2.中心对称是对两个图形而言的,表示两个图形之间关系。
3.中心对称只有一个对称中心。
自主学习二
阅读课本本课时中心对称的性质及图3-20,解决下列问题:
1.图3-20中对应点的连线都经过点O,图中相等的线段有哪些?
AB=A’B’
BC=B’C’
AC=A’C’
OA=OA’
OB=OB’
OC=OC’
2.
△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系?
A′
B′
C′
A
B
C
O
(1)
OA=OA′、OB=OB′、
OC=OC′
(2)△ABC≌△A′B′C′
归纳总结:
1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分。
2.成中心对称的两个图形是全等图形,对应角相等,对应线段平行(或在同一直线上)且相等。
自主训练
如图△A′B′C′
与△ABC
关于点O是成中心对称,下列说法不正确是(
)
A,S△ABC=S
△ABC
B,A′B′=AB,
B′C′
=BC
C,
A′B′∥AB,
B′C′
∥
BC
D,S△ACO=S
△A′B′O
A′
B′
C′
A
B
C
O
D
自主学习三
阅读课本本课时例题和议一仪中的内容,解决下列问题:
1.教材例题中的画图依据是什么?中心对称图形的定义是什么?
成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分。
2.
仿照例题中的方法,画出四边形ABCD关于O点的对称图形。
A
B
C
D
O
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对称点,再顺次连接各对应点即可。
把一个图形绕某个点旋转180?,如果旋转后图形能与原来图形重合,那么这个图形叫做中心对称图形,这个点叫做他的对称中心。
做法展示:
A
B
C
D
O
1.连接AO并延长到A',使OA'=OA,得到点A的对应点A';
A'
B'
C'
D'
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
合作交流:
根据中心对称的性质画已知图形关于某点成中心对称的图形的步骤是什么?
1.确定关键点:将各关键点(如多边形的各顶点)和对称中心连接并延长。
2.确定对应点:在延长线上取各关键点的对应点,使对应点到对称中心的
距离和关键点到对称中心的距离相等。
3.连线:按照原图将各对应点顺次连接即可得到所要画的图形。
自主训练
1,如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O。
A
B
C
A′
B′
C′
解法示范:
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O
即为所求(如图)。
A
B
C
A′
B′
C′
O
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图)。
O
A
B
C
A′
B′
C′
如果限制只用尺规作图,我们选方法二。
课时测评
√
√
(1)
(2)
(3)
√
(4)
1,下列图形中哪些是中心对称图形?
×
课时测评
2.如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高为________.
解析:设AB边上的高为h,因为△AOB的面积是12,AB=3,易得h=8.
又因为△AOB与△DOC成中心对称,△COD≌△AOB,所以△DOC中CD边上的高是8.
8
课时测评
3.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3。
3
轴
对
称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
当堂练习
1.判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.(
)
(2)成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形.
(
)
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形.
(
)
√
√
×
当堂练习
2.下列图形中是中心对称图形而不是轴对称图形的是
(
)
A
.
平行四边形
B.
矩形
C
.
菱形
D
.
正方形
A
A′
B′
C′
O
A
B
C
3.如图,已知等边三角形ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
总结归纳
中心对称和
中心对称图形
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
课后作业
1.完成本课时对应的课后习题。
2.完成本课时对应的导学测评和基础训练相关练习。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
