2020-2021学年北师大版八年级数学下册课课练 3. 1 图形的平移(第3课时)(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册课课练 3. 1 图形的平移(第3课时)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 575.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 14:29:22 | ||
图片预览




文档简介
1 第3课时 平面直角坐标系中的平移(2)
(A卷)
知识点 依次沿两个坐标轴方向平移后所得到的图形与原图形之间的关系
1.[2020·台州]
如图3-1-19,把△ABC先向右平移3个单位长度,再向上平移2个单位长度得到△DEF,则顶点C(0,-1)的对应点F的坐标为
( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
图3-1-19
图3-1-20
2.[2019·海南]
如图3-1-20,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为
( )
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
3.如图3-1-21,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1的位置,则a+b的值为
( )
A.2
B.3
C.4
D.5
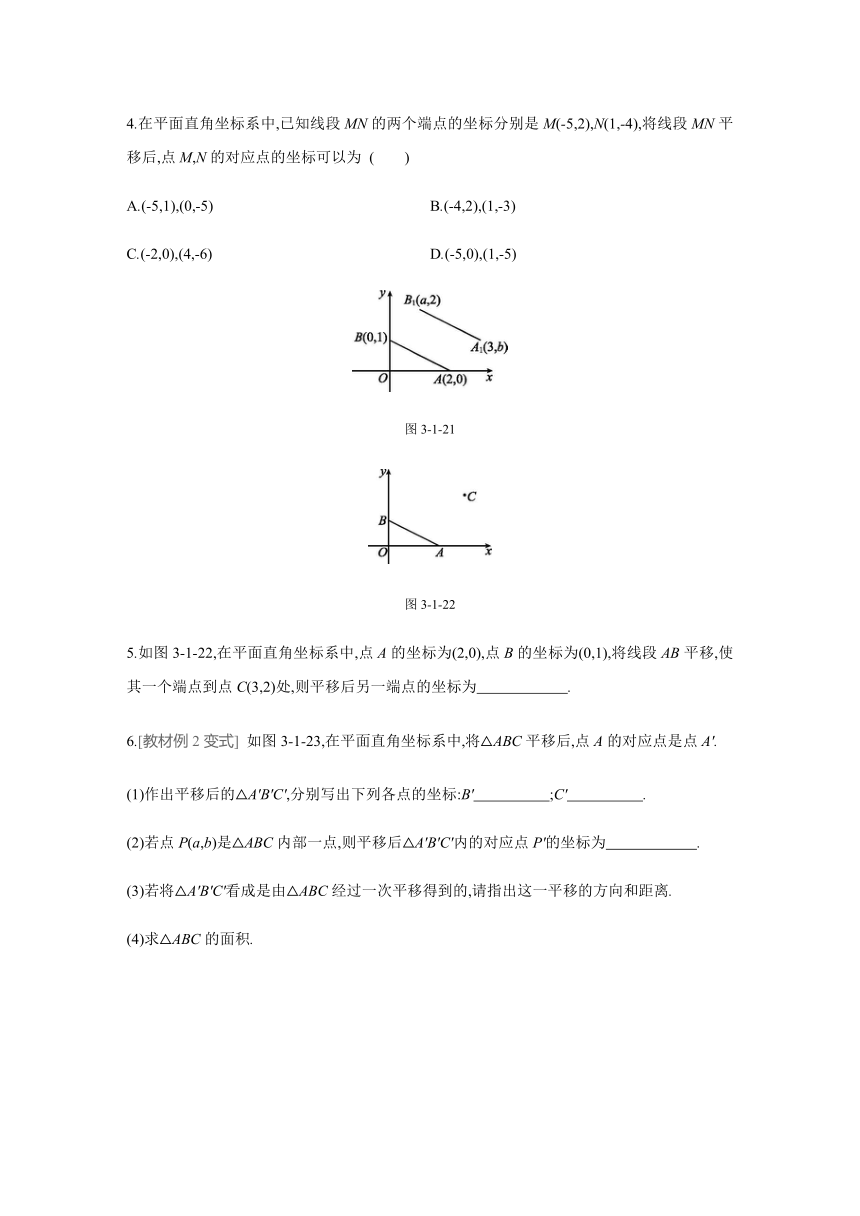
4.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-5,2),N(1,-4),将线段MN平移后,点M,N的对应点的坐标可以为
( )
A.(-5,1),(0,-5)
B.(-4,2),(1,-3)
C.(-2,0),(4,-6)
D.(-5,0),(1,-5)
图3-1-21
图3-1-22
5.如图3-1-22,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到点C(3,2)处,则平移后另一端点的坐标为 .?
6.[教材例2变式]
如图3-1-23,在平面直角坐标系中,将△ABC平移后,点A的对应点是点A'.
(1)作出平移后的△A'B'C',分别写出下列各点的坐标:B' ;C' .?
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C'内的对应点P'的坐标为 .?
(3)若将△A'B'C'看成是由△ABC经过一次平移得到的,请指出这一平移的方向和距离.
(4)求△ABC的面积.
图3-1-23
7.如图3-1-24所示,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着折线OABCO移动(即沿着长方形移动一周).
(1)点B的坐标是 ;?
(2)当点P移动了4秒时,在图中描出此时点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
图3-1-24
(B卷)
命题点
1 由坐标变化规律求解相关点的坐标或进行计算
1.在平面直角坐标系中,将点P(-2,1)先向右平移3个单位长度,再向上平移4个单位长度得到的点的坐标是( )
A.(2,4)
B.(1,5)
C.(1,-3)
D.(-5,5)
2.2019·信阳浉河区月考
将点A先向下平移3个单位长度,再向右平移4个单位长度,得到点A′(-3,-6),则点A的坐标为( )
A.(-7,3)
B.(6,-10)
C.(-7,-3)
D.(-1,-10)
3.2019·海南
如图3-1-21,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
图3-1-21
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
4.如图3-1-22,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
图3-1-22
A.2
B.3
C.4
D.5
5.已知△ABC内一点P(a,b)经过平移后的对应点为P′(c,d),顶点A(-2,2)在经过此次平移后的对应点为A′(5,-4),则a-b-c+d的值为( )
A.13
B.-13
C.1
D.-1
6.2020·南阳邓州一模
如图3-1-23,在平面直角坐标系中,等边三角形OAB的边长为4,点A在第二象限内,将△OAB沿射线AO平移,平移后点A′的横坐标为4
,则点B′的坐标为________.
图3-1-23
方法点拨(6题)
在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
命题点
2 与坐标系有关的作图与计算
7.如图3-1-24,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
图3-1-24
8.2020·孝感云梦期中
如图3-1-25,△ABC的三个顶点坐标分别为A(-3,1),B(1,-2),C(2,2),△ABC内有一点P(m,n)经过平移后的对应点为P1(m-1,n+2),将△ABC做同样平移得到△A1B1C1.
(1)写出A1,B1,C1三点的坐标;
(2)求△A1B1C1的面积.
图3-1-25
9.△ABC的顶点坐标分别为A(2,-1),B(1,-3),C(4,-3.5).
(1)在平面直角坐标系中画出△ABC;
(2)把△A1B1C1先向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1各顶点的坐标,并在平面直角坐标系中画出△A1B1C1;
(3)求出△A1B1C1的面积.
图3-1-26
方法点拨(9题)
在平面直角坐标系中解决与面积有关的问题时,通常将所求图形补成易求面积的图形或将图形分割成易求面积的图形进行求解.
命题点
3 与坐标平移变化有关的规律探究题
10.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到点(0,1),然后按图3-1-27中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动1个单位长度,那么第35秒时跳蚤所在位置的坐标是( )
图3-1-27
A.(4,0)
B.(5,0)
C.(0,5)
D.(5,5)
11.2020·南宁武鸣期中如图3-1-28,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动1个单位长度,由此得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0)……那么点A2020的坐标为( )
图3-1-28
A.(2020,1)
B.(2020,0)
C.(1010,1)
D.(1010,0)
12.2020·武汉江岸区月考
在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4……这样依次得到点A1,A2,A3,…,An.若点A1的坐标为(a,b),则点A2020的坐标为( )
A.(a,b)
B.(-b+1,a+1)
C.(-a,-b+2)
D.(b-1,-a+1)
13.如图3-1-29所示,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—A—B—C—O的路线移动(即沿着长方形移动一周).
(1)点B的坐标是________;
(2)当点P移动了4秒时,描出此时点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
图3-1-29
解题突破(13题)
你能确定点P到x轴的距离为5个单位长度时,有哪几种情况吗?
教师详解详析
1.D [解析]
∵把△ABC先向右平移3个单位长度,再向上平移2个单位长度得到△DEF,点C(0,-1),∴点C的对应点F的坐标为(0+3,-1+2),即F(3,1).
2.C [解析]
由点A(2,1)平移后的对应点A1的坐标为(-2,2)可得线段AB的平移过程是:向左平移4个单位长度,向上平移1个单位长度,
所以点B的对应点B1的坐标为(-1,0).
故选C.
3.A [解析]
由点B平移前后的纵坐标分别为1,2,可得点B向上平移了1个单位长度,由点A平移前后的横坐标分别为2,3,可得点A向右平移了1个单位长度,由此得线段AB的平移过程是向上平移1个单位长度,再向右平移1个单位长度,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.
4.C [解析]
先由点M及其对应点的坐标得出平移的方向、距离,再根据坐标系中点的坐标的平移规律得出点C的对应点.由M(-5,2)对应(-2,0)知点N(1,-4)的对应点应该是(4,-6),所以C选项正确.
5.(1,3)或(5,1) [解析]
分两种情况:①当点A平移到点C时,∵C(3,2),A(2,0),∴点A的横坐标增加了1,纵坐标增加了2,则平移后点B的坐标变为(1,3);②当点B平移到点C时,∵C(3,2),B(0,1),∴点B的横坐标增加了3,纵坐标增加了1,∴平移后点A的坐标变为(5,1).
6.解:(1)如图:
(-2,-2) (-1,-1)
(2)(a-4,b-2)
(3)连接AA',可知AA'==2,
因此,若将△A'B'C'看成是由△ABC经过一次平移得到的,则这一平移的方向是由点A到点A'的方向,平移的距离是2个单位长度.
(4)S△ABC=2×3-×2×2-×1×3-×1×1=2.
7.解:(1)(4,6)
(2)点P的移动速度为每秒2个单位长度,当点P移动了4秒时,共移动了8个单位长度,此时点P的坐标为(4,4),位于AB上,描点略.
(3)根据题意,当点P到x轴的距离为5个单位长度时,有两种情况:①若点P在AB上,则点P移动了4+5=9(个)单位长度,此时点P移动了=4.5(秒);②若点P在OC上,则点P移动了4+6+4+1=15(个)单位长度,此时点P移动了=7.5(秒).
综上所述,当点P到x轴的距离为5个单位长度时,点P移动的时间为4.5秒或7.5秒.
教师详解详析
1.B 2.C 3.C
4.A [解析]
由点A平移前后的横坐标分别为2和3,可知点A向右平移了1个单位长度;由点B平移前后的纵坐标分别为1和2,可知点B向上平移了1个单位长度,因而可得线段AB平移至A1B1的过程:向右平移1个单位长度,向上平移1个单位长度.按此平移规律,可得a=0+1=1,b=0+1=1,∴a+b=1+1=2.故选A.
5.B [解析]
∵A(-2,2)在经过此次平移后的对应点A'的坐标为(5,-4),
∴△ABC的平移规律为:向右平移7个单位长度,向下平移6个单位长度.
∵点P(a,b)经过平移后的对应点为P'(c,d),
∴a+7=c,b-6=d,∴a-c=-7,b-d=6,
∴a-b-c+d=a-c-(b-d)=-7-6=-13.故选B.
6.(6,-2) [解析]
∵等边三角形OAB的边长为4,点A在第二象限内,
∴点A的坐标为(-2,2).
∵平移后点A'的横坐标为4,纵坐标为-4,
∴平移规律为向右平移6个单位长度,向下平移6个单位长度.
∵点B的坐标为(0,4),
∴点B'的坐标为(6,-2).
7.解:(1)∵A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF,
∴D(2,9),E(1,5),F(4,6).
(2)连接AD,由图可知AD==5.
∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是点A到点D的方向(或点B到点E的方向或点C到点F的方向),平移的距离是5个单位长度.
8.解:(1)如图所示:
A1(-4,3),B1(0,0),C1(1,4).
(2)△A1B1C1的面积=4×5-×1×4-×1×5-×3×4=20-2--6=.
9.解:(1)在平面直角坐标系中描出A,B,C三点,顺次连接,得到△ABC,如图.
(2)把△A1B1C1先向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,即△ABC向上平移3个单位长度,向左平移4个单位长度,得到△A1B1C1,按照平移中点的坐标变化规律:横坐标右移加,左移减;纵坐标上移加,下移减,可得A1(-2,2),B1(-3,0),C1(0,-0.5),画出△A1B1C1如图所示.
(3)如图,把△A1B1C1补成长方形再把周边的三角形的面积减去,求得△A1B1C1的面积=3×2.5-1-2.5-0.75=3.25.∴△A1B1C1的面积为3.25.
10.B [解析]
方法一:跳蚤跳动的速度是每秒跳动1个单位长度,到点(0,1),(1,1),(1,0)用的秒数分别是1秒、2秒、3秒,到点(2,0)用4秒,到点(2,2)用6秒,到点(0,2)用8秒,到点(0,3)用9秒,到点(3,3)用12秒,到点(3,0)用15秒,依次类推,到点(5,0)用35秒.故第35秒时跳蚤所在位置的坐标是(5,0).方法二:根据题意,结合图形我们可以发现第n(n+2)秒时跳蚤所在位置的坐标是
35=5×(5+2),所以第35秒时跳蚤所在位置的坐标为(5,0).
11.D [解析]
由图象可知:纵坐标每四个点循环一次,而2020=505×4,
故点A2020的纵坐标与点A4的纵坐标相同,都等于0;
由A4(2,0),A8(4,0),A12(6,0),…,
可得到规律A4n(2n,0)(n为不为0的自然数),
当n=505时,A2020(1010,0).
12.D [解析]
观察发现:A1(a,b),A2(-b+1,a+1),A3(-a,-b+2),A4(b-1,-a+1),A5(a,b),A6(-b+1,a+1)…
∴依此类推,每4个点为一个循环组依次循环.
∵2020÷4=505,
∴点A2020的坐标与点A4的坐标相同,为(b-1,-a+1).
13.解:(1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行,故点B的坐标为(4,6).
(2)根据题意,知点P的运动速度为每秒2个单位长度,当点P移动了4秒时,共移动了8个单位长度,此时点P的坐标为(4,4),位于AB上,描点略.
(3)根据题意,点P到x轴的距离为5个单位长度时,有两种情况:
①若点P在AB上,则点P移动了4+5=9(个)单位长度,此时点P移动了9÷2=4.5(秒);
②若点P在OC上,则点P移动了4+6+4+1=15(个)单位长度,此时点P移动了15÷2=7.5(秒).
综上所述,点P移动的时间为4.5秒或7.5秒.
(A卷)
知识点 依次沿两个坐标轴方向平移后所得到的图形与原图形之间的关系
1.[2020·台州]
如图3-1-19,把△ABC先向右平移3个单位长度,再向上平移2个单位长度得到△DEF,则顶点C(0,-1)的对应点F的坐标为
( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
图3-1-19
图3-1-20
2.[2019·海南]
如图3-1-20,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为
( )
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
3.如图3-1-21,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1的位置,则a+b的值为
( )
A.2
B.3
C.4
D.5
4.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-5,2),N(1,-4),将线段MN平移后,点M,N的对应点的坐标可以为
( )
A.(-5,1),(0,-5)
B.(-4,2),(1,-3)
C.(-2,0),(4,-6)
D.(-5,0),(1,-5)
图3-1-21
图3-1-22
5.如图3-1-22,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到点C(3,2)处,则平移后另一端点的坐标为 .?
6.[教材例2变式]
如图3-1-23,在平面直角坐标系中,将△ABC平移后,点A的对应点是点A'.
(1)作出平移后的△A'B'C',分别写出下列各点的坐标:B' ;C' .?
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C'内的对应点P'的坐标为 .?
(3)若将△A'B'C'看成是由△ABC经过一次平移得到的,请指出这一平移的方向和距离.
(4)求△ABC的面积.
图3-1-23
7.如图3-1-24所示,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着折线OABCO移动(即沿着长方形移动一周).
(1)点B的坐标是 ;?
(2)当点P移动了4秒时,在图中描出此时点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
图3-1-24
(B卷)
命题点
1 由坐标变化规律求解相关点的坐标或进行计算
1.在平面直角坐标系中,将点P(-2,1)先向右平移3个单位长度,再向上平移4个单位长度得到的点的坐标是( )
A.(2,4)
B.(1,5)
C.(1,-3)
D.(-5,5)
2.2019·信阳浉河区月考
将点A先向下平移3个单位长度,再向右平移4个单位长度,得到点A′(-3,-6),则点A的坐标为( )
A.(-7,3)
B.(6,-10)
C.(-7,-3)
D.(-1,-10)
3.2019·海南
如图3-1-21,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
图3-1-21
A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
4.如图3-1-22,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
图3-1-22
A.2
B.3
C.4
D.5
5.已知△ABC内一点P(a,b)经过平移后的对应点为P′(c,d),顶点A(-2,2)在经过此次平移后的对应点为A′(5,-4),则a-b-c+d的值为( )
A.13
B.-13
C.1
D.-1
6.2020·南阳邓州一模
如图3-1-23,在平面直角坐标系中,等边三角形OAB的边长为4,点A在第二象限内,将△OAB沿射线AO平移,平移后点A′的横坐标为4
,则点B′的坐标为________.
图3-1-23
方法点拨(6题)
在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
命题点
2 与坐标系有关的作图与计算
7.如图3-1-24,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
图3-1-24
8.2020·孝感云梦期中
如图3-1-25,△ABC的三个顶点坐标分别为A(-3,1),B(1,-2),C(2,2),△ABC内有一点P(m,n)经过平移后的对应点为P1(m-1,n+2),将△ABC做同样平移得到△A1B1C1.
(1)写出A1,B1,C1三点的坐标;
(2)求△A1B1C1的面积.
图3-1-25
9.△ABC的顶点坐标分别为A(2,-1),B(1,-3),C(4,-3.5).
(1)在平面直角坐标系中画出△ABC;
(2)把△A1B1C1先向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1各顶点的坐标,并在平面直角坐标系中画出△A1B1C1;
(3)求出△A1B1C1的面积.
图3-1-26
方法点拨(9题)
在平面直角坐标系中解决与面积有关的问题时,通常将所求图形补成易求面积的图形或将图形分割成易求面积的图形进行求解.
命题点
3 与坐标平移变化有关的规律探究题
10.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到点(0,1),然后按图3-1-27中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动1个单位长度,那么第35秒时跳蚤所在位置的坐标是( )
图3-1-27
A.(4,0)
B.(5,0)
C.(0,5)
D.(5,5)
11.2020·南宁武鸣期中如图3-1-28,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动1个单位长度,由此得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0)……那么点A2020的坐标为( )
图3-1-28
A.(2020,1)
B.(2020,0)
C.(1010,1)
D.(1010,0)
12.2020·武汉江岸区月考
在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4……这样依次得到点A1,A2,A3,…,An.若点A1的坐标为(a,b),则点A2020的坐标为( )
A.(a,b)
B.(-b+1,a+1)
C.(-a,-b+2)
D.(b-1,-a+1)
13.如图3-1-29所示,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—A—B—C—O的路线移动(即沿着长方形移动一周).
(1)点B的坐标是________;
(2)当点P移动了4秒时,描出此时点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
图3-1-29
解题突破(13题)
你能确定点P到x轴的距离为5个单位长度时,有哪几种情况吗?
教师详解详析
1.D [解析]
∵把△ABC先向右平移3个单位长度,再向上平移2个单位长度得到△DEF,点C(0,-1),∴点C的对应点F的坐标为(0+3,-1+2),即F(3,1).
2.C [解析]
由点A(2,1)平移后的对应点A1的坐标为(-2,2)可得线段AB的平移过程是:向左平移4个单位长度,向上平移1个单位长度,
所以点B的对应点B1的坐标为(-1,0).
故选C.
3.A [解析]
由点B平移前后的纵坐标分别为1,2,可得点B向上平移了1个单位长度,由点A平移前后的横坐标分别为2,3,可得点A向右平移了1个单位长度,由此得线段AB的平移过程是向上平移1个单位长度,再向右平移1个单位长度,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.
4.C [解析]
先由点M及其对应点的坐标得出平移的方向、距离,再根据坐标系中点的坐标的平移规律得出点C的对应点.由M(-5,2)对应(-2,0)知点N(1,-4)的对应点应该是(4,-6),所以C选项正确.
5.(1,3)或(5,1) [解析]
分两种情况:①当点A平移到点C时,∵C(3,2),A(2,0),∴点A的横坐标增加了1,纵坐标增加了2,则平移后点B的坐标变为(1,3);②当点B平移到点C时,∵C(3,2),B(0,1),∴点B的横坐标增加了3,纵坐标增加了1,∴平移后点A的坐标变为(5,1).
6.解:(1)如图:
(-2,-2) (-1,-1)
(2)(a-4,b-2)
(3)连接AA',可知AA'==2,
因此,若将△A'B'C'看成是由△ABC经过一次平移得到的,则这一平移的方向是由点A到点A'的方向,平移的距离是2个单位长度.
(4)S△ABC=2×3-×2×2-×1×3-×1×1=2.
7.解:(1)(4,6)
(2)点P的移动速度为每秒2个单位长度,当点P移动了4秒时,共移动了8个单位长度,此时点P的坐标为(4,4),位于AB上,描点略.
(3)根据题意,当点P到x轴的距离为5个单位长度时,有两种情况:①若点P在AB上,则点P移动了4+5=9(个)单位长度,此时点P移动了=4.5(秒);②若点P在OC上,则点P移动了4+6+4+1=15(个)单位长度,此时点P移动了=7.5(秒).
综上所述,当点P到x轴的距离为5个单位长度时,点P移动的时间为4.5秒或7.5秒.
教师详解详析
1.B 2.C 3.C
4.A [解析]
由点A平移前后的横坐标分别为2和3,可知点A向右平移了1个单位长度;由点B平移前后的纵坐标分别为1和2,可知点B向上平移了1个单位长度,因而可得线段AB平移至A1B1的过程:向右平移1个单位长度,向上平移1个单位长度.按此平移规律,可得a=0+1=1,b=0+1=1,∴a+b=1+1=2.故选A.
5.B [解析]
∵A(-2,2)在经过此次平移后的对应点A'的坐标为(5,-4),
∴△ABC的平移规律为:向右平移7个单位长度,向下平移6个单位长度.
∵点P(a,b)经过平移后的对应点为P'(c,d),
∴a+7=c,b-6=d,∴a-c=-7,b-d=6,
∴a-b-c+d=a-c-(b-d)=-7-6=-13.故选B.
6.(6,-2) [解析]
∵等边三角形OAB的边长为4,点A在第二象限内,
∴点A的坐标为(-2,2).
∵平移后点A'的横坐标为4,纵坐标为-4,
∴平移规律为向右平移6个单位长度,向下平移6个单位长度.
∵点B的坐标为(0,4),
∴点B'的坐标为(6,-2).
7.解:(1)∵A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF,
∴D(2,9),E(1,5),F(4,6).
(2)连接AD,由图可知AD==5.
∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是点A到点D的方向(或点B到点E的方向或点C到点F的方向),平移的距离是5个单位长度.
8.解:(1)如图所示:
A1(-4,3),B1(0,0),C1(1,4).
(2)△A1B1C1的面积=4×5-×1×4-×1×5-×3×4=20-2--6=.
9.解:(1)在平面直角坐标系中描出A,B,C三点,顺次连接,得到△ABC,如图.
(2)把△A1B1C1先向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,即△ABC向上平移3个单位长度,向左平移4个单位长度,得到△A1B1C1,按照平移中点的坐标变化规律:横坐标右移加,左移减;纵坐标上移加,下移减,可得A1(-2,2),B1(-3,0),C1(0,-0.5),画出△A1B1C1如图所示.
(3)如图,把△A1B1C1补成长方形再把周边的三角形的面积减去,求得△A1B1C1的面积=3×2.5-1-2.5-0.75=3.25.∴△A1B1C1的面积为3.25.
10.B [解析]
方法一:跳蚤跳动的速度是每秒跳动1个单位长度,到点(0,1),(1,1),(1,0)用的秒数分别是1秒、2秒、3秒,到点(2,0)用4秒,到点(2,2)用6秒,到点(0,2)用8秒,到点(0,3)用9秒,到点(3,3)用12秒,到点(3,0)用15秒,依次类推,到点(5,0)用35秒.故第35秒时跳蚤所在位置的坐标是(5,0).方法二:根据题意,结合图形我们可以发现第n(n+2)秒时跳蚤所在位置的坐标是
35=5×(5+2),所以第35秒时跳蚤所在位置的坐标为(5,0).
11.D [解析]
由图象可知:纵坐标每四个点循环一次,而2020=505×4,
故点A2020的纵坐标与点A4的纵坐标相同,都等于0;
由A4(2,0),A8(4,0),A12(6,0),…,
可得到规律A4n(2n,0)(n为不为0的自然数),
当n=505时,A2020(1010,0).
12.D [解析]
观察发现:A1(a,b),A2(-b+1,a+1),A3(-a,-b+2),A4(b-1,-a+1),A5(a,b),A6(-b+1,a+1)…
∴依此类推,每4个点为一个循环组依次循环.
∵2020÷4=505,
∴点A2020的坐标与点A4的坐标相同,为(b-1,-a+1).
13.解:(1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行,故点B的坐标为(4,6).
(2)根据题意,知点P的运动速度为每秒2个单位长度,当点P移动了4秒时,共移动了8个单位长度,此时点P的坐标为(4,4),位于AB上,描点略.
(3)根据题意,点P到x轴的距离为5个单位长度时,有两种情况:
①若点P在AB上,则点P移动了4+5=9(个)单位长度,此时点P移动了9÷2=4.5(秒);
②若点P在OC上,则点P移动了4+6+4+1=15(个)单位长度,此时点P移动了15÷2=7.5(秒).
综上所述,点P移动的时间为4.5秒或7.5秒.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
