2020--2021学年北师大版七年级数学下册4.1: 第4课时 三角形的高(共18张ppt)
文档属性
| 名称 | 2020--2021学年北师大版七年级数学下册4.1: 第4课时 三角形的高(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
第四章
三角形
1
第4课时
三角形的高
课堂小结
例题讲解
知识回顾
随堂演练
获取新知
知识回顾
1.什么是三角形的中线?什么是三角形的角平分线?
2.三角形的三条中线、角平分线相交于一点吗?
这一交点在三角形的内部还是外部?
根据自己的理解回答
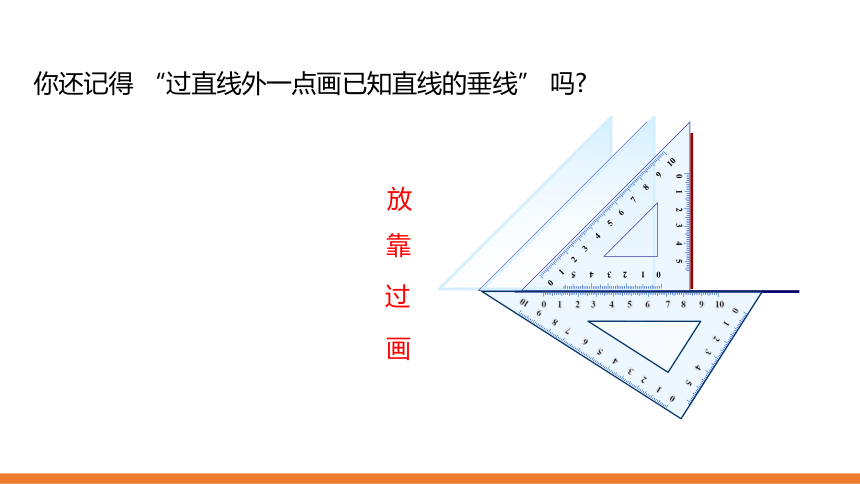
你还记得
“过直线外一点画已知直线的垂线”
吗?
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
放
靠
过
画
获取新知
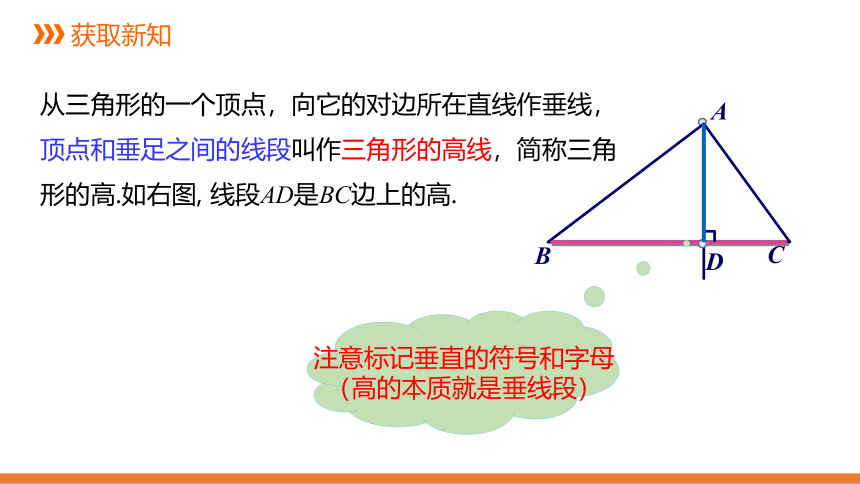
从三角形的一个顶点,向它的对边所在直线作垂线,
顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.如右图,
线段AD是BC边上的高.
A
B
C
D
注意标记垂直的符号和字母
(高的本质就是垂线段)
做一做
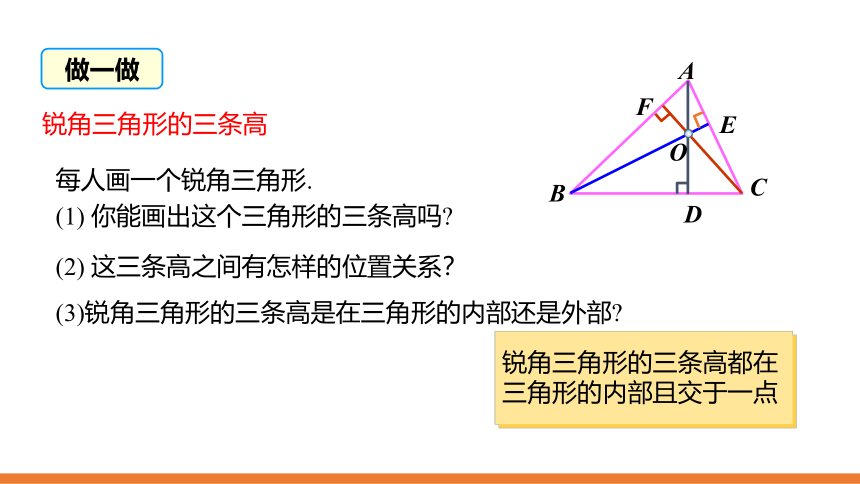
锐角三角形的三条高
每人画一个锐角三角形.
(1)
你能画出这个三角形的三条高吗?
(2)
这三条高之间有怎样的位置关系?
(3)锐角三角形的三条高是在三角形的内部还是外部?
O
A
B
C
D
E
F
锐角三角形的三条高都在三角形的内部且交于一点
议一议
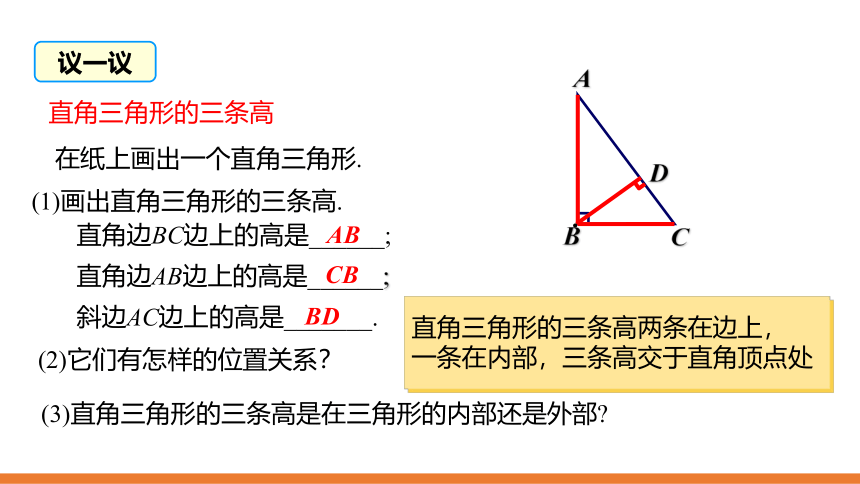
直角三角形的三条高
在纸上画出一个直角三角形.
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
斜边AC边上的高是_______.
BD
(3)直角三角形的三条高是在三角形的内部还是外部?
A
B
C
D
●
直角三角形的三条高两条在边上,
一条在内部,三条高交于直角顶点处
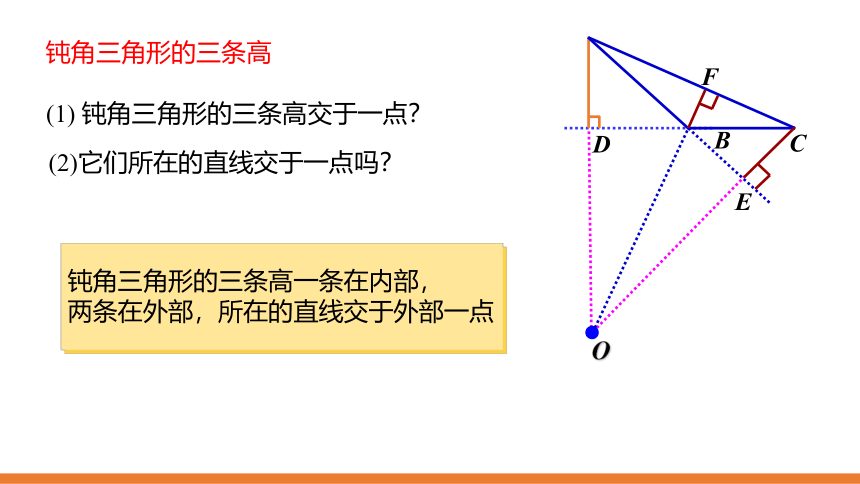
钝角三角形的三条高
(1)
钝角三角形的三条高交于一点?
(2)它们所在的直线交于一点吗?
B
C
D
E
F
O
钝角三角形的三条高一条在内部,
两条在外部,所在的直线交于外部一点
三角形的三条高的特性:
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
三条高所在直线的交点位置
钝角三角形
直角三角形
锐角三角形
例题讲解
例1
画出下图中△ABC的三条高.(要标明字母,不写画法)
解:如图所示.
例2
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD=100°.
随堂演练
1.下列各组图形中,哪一组图形中AD是△ABC
的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
2.
如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上都有可能
C
3.
如图,在△ABC中,AD是高,∠B=40°,∠CAD=20°,
则∠BAC的度数为
( )
A.20°
B.30°
C.50°
D.60°
B
4.
如图,在△ABC中,BC边上的高是________;
在△BCE中,BE边上的高是________;
在△ACD中,AC边上的高是________.
AF
CE
CD
5.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=_______.
50°
1
2
A
C
D
B
E
6.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
解:
∵
AD是△ABC的高,
∴∠ADC=90°,
∵∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-(∠ADC+∠C)=50°
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=
9°.
B
A
C
D
E
7.
如图,已知△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.试说明:BG=DE+DF.
解:如图,连接AD,因为S△ABC=S△ABD+S△ADC,
所以
AC·BG=
AB·DE+
AC·DF.
又因为AB=AC,
所以BG=DE+DF.
课堂小结
三角形的高
锐角三角形的三条高
都在三角形的内部.
高的定义(垂线段)
高的性质
直角三角形的三条高
交于直角顶点.
钝角三角形的三条高
所在直线交于一点.
第四章
三角形
1
第4课时
三角形的高
课堂小结
例题讲解
知识回顾
随堂演练
获取新知
知识回顾
1.什么是三角形的中线?什么是三角形的角平分线?
2.三角形的三条中线、角平分线相交于一点吗?
这一交点在三角形的内部还是外部?
根据自己的理解回答
你还记得
“过直线外一点画已知直线的垂线”
吗?
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
放
靠
过
画
获取新知
从三角形的一个顶点,向它的对边所在直线作垂线,
顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.如右图,
线段AD是BC边上的高.
A
B
C
D
注意标记垂直的符号和字母
(高的本质就是垂线段)
做一做
锐角三角形的三条高
每人画一个锐角三角形.
(1)
你能画出这个三角形的三条高吗?
(2)
这三条高之间有怎样的位置关系?
(3)锐角三角形的三条高是在三角形的内部还是外部?
O
A
B
C
D
E
F
锐角三角形的三条高都在三角形的内部且交于一点
议一议
直角三角形的三条高
在纸上画出一个直角三角形.
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
斜边AC边上的高是_______.
BD
(3)直角三角形的三条高是在三角形的内部还是外部?
A
B
C
D
●
直角三角形的三条高两条在边上,
一条在内部,三条高交于直角顶点处
钝角三角形的三条高
(1)
钝角三角形的三条高交于一点?
(2)它们所在的直线交于一点吗?
B
C
D
E
F
O
钝角三角形的三条高一条在内部,
两条在外部,所在的直线交于外部一点
三角形的三条高的特性:
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
三条高所在直线的交点位置
钝角三角形
直角三角形
锐角三角形
例题讲解
例1
画出下图中△ABC的三条高.(要标明字母,不写画法)
解:如图所示.
例2
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD=100°.
随堂演练
1.下列各组图形中,哪一组图形中AD是△ABC
的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
2.
如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上都有可能
C
3.
如图,在△ABC中,AD是高,∠B=40°,∠CAD=20°,
则∠BAC的度数为
( )
A.20°
B.30°
C.50°
D.60°
B
4.
如图,在△ABC中,BC边上的高是________;
在△BCE中,BE边上的高是________;
在△ACD中,AC边上的高是________.
AF
CE
CD
5.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=_______.
50°
1
2
A
C
D
B
E
6.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
解:
∵
AD是△ABC的高,
∴∠ADC=90°,
∵∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-(∠ADC+∠C)=50°
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=
9°.
B
A
C
D
E
7.
如图,已知△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.试说明:BG=DE+DF.
解:如图,连接AD,因为S△ABC=S△ABD+S△ADC,
所以
AC·BG=
AB·DE+
AC·DF.
又因为AB=AC,
所以BG=DE+DF.
课堂小结
三角形的高
锐角三角形的三条高
都在三角形的内部.
高的定义(垂线段)
高的性质
直角三角形的三条高
交于直角顶点.
钝角三角形的三条高
所在直线交于一点.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
