6.3向心加速度 课件 24张PPT
文档属性
| 名称 | 6.3向心加速度 课件 24张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-08 16:00:47 | ||
图片预览







文档简介
6.3 向心加速度
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为 0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
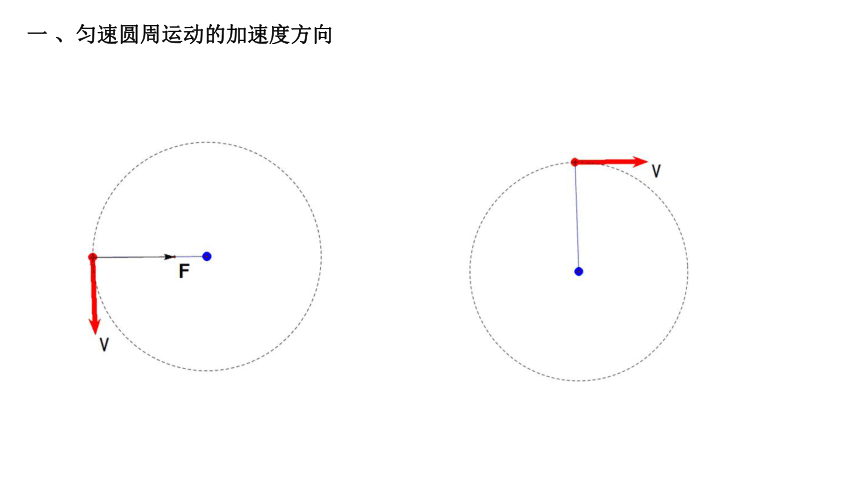
一 、匀速圆周运动的加速度方向
物体做匀速圆周运动时,所受合力提供向心力,合力 的方向总是指向圆心,如图 6.3-1 所示。根据牛顿第二定律,物体运动的加速度方向与它所受合力的方向相同。因此,物体做匀速圆周运动时的加速度总指向圆心,我们把它叫作向心加速度(centripetal acceleration)。
我们知道,加速度是速度的变化率。在研究直线运动时,我们曾通过分析速度变化的情况,得出直线运动的加速度大小和方向。其实,在研究匀速圆周运动时,同样可以通过这种办法来确定加速度的方向。用运动学的方法求向心加速度的方向,在本节后的“拓展学习”中会涉及。
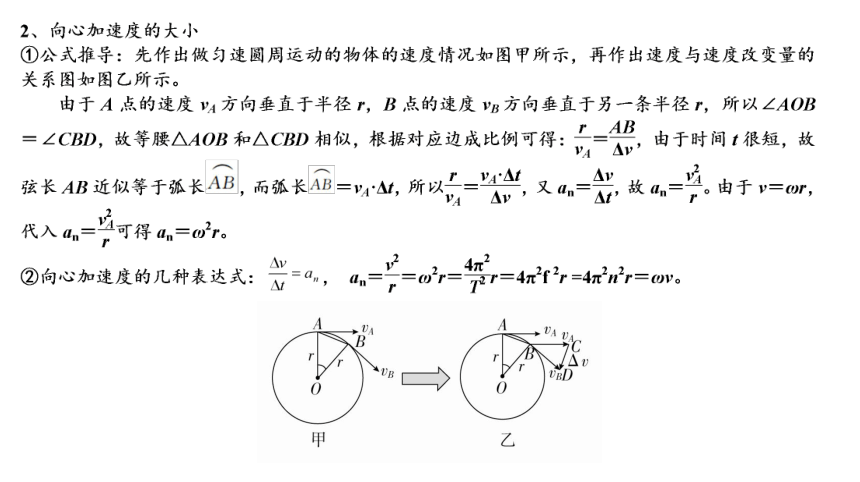
二、匀速圆周运动的加速度大小
(一)从牛顿运动定律的角度看向心加速度
(二)从运动学的角度看向心加速度
(1)直线运动
(2)圆周运动
(三)对向心加速度的理解
3、对向心加速度的理解
(1) 物理意义:描述匀速圆周运动中线速度改变的快慢,只能表示速度方向变化的快慢,不表示速度大小变化的快慢。
(2)方向特点
①指向圆心:无论是匀速圆周运动,还是变速圆周运动,向心加速度的方向都指向圆心(或者说与线速度方向垂直)。
②时刻改变:无论向心加速度的大小是否变化,向心加速度的方向随线速度方向的改变时刻改变,所以圆周运动的向心加速度是时刻改变的。
(3)“匀速圆周运动中的“变”与“不变”
① “不变”量:匀速圆周运动的角速度、周期、转速不变,线速度、加速度这两个矢量的大小不变。
②“变化”量:匀速圆周运动的线速度、加速度这两个矢量的方向时刻改变,故它们在时刻变化。
例题:如图 6.3-3 所示,在长为 l 的细绳下端拴一个质量 为 m 的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。 当绳子跟竖直方向的夹角为 θ 时,小球运动的向心加速 度 an 的大小为多少?通过计算说明 :要增大夹角 θ,应 该增大小球运动的角速度 ω。
三、向心加速度公式也适用于非匀速圆周运动.
1、变速圆周运动的向心加速度
做变速圆周运动的物体,加速度一般情况下不指向圆心,该加速度有两个分量:
一是向心加速度,
二是切向加速度.
(1)向心加速度表示速度方向变化的快慢,
(2)切向加速度表示速度大小变化的快慢.
所以变速圆周运动中,向心加速度的方向也总是指向圆心.对于变速圆周运动,如图所示,物体加速度的方向不再指向圆心,但其中一个分加速度的方向指向圆心,为向心加速度,仍满足公式an,其作用仍然是改变速度的方向。
(2)它们的线速度大小相等,在相同时间内甲与圆心的连线扫过的角度比乙的大。
(1)它们的角速度相等,乙的线速度小。
四、传动装置
课堂练习
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为 0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
一 、匀速圆周运动的加速度方向
物体做匀速圆周运动时,所受合力提供向心力,合力 的方向总是指向圆心,如图 6.3-1 所示。根据牛顿第二定律,物体运动的加速度方向与它所受合力的方向相同。因此,物体做匀速圆周运动时的加速度总指向圆心,我们把它叫作向心加速度(centripetal acceleration)。
我们知道,加速度是速度的变化率。在研究直线运动时,我们曾通过分析速度变化的情况,得出直线运动的加速度大小和方向。其实,在研究匀速圆周运动时,同样可以通过这种办法来确定加速度的方向。用运动学的方法求向心加速度的方向,在本节后的“拓展学习”中会涉及。
二、匀速圆周运动的加速度大小
(一)从牛顿运动定律的角度看向心加速度
(二)从运动学的角度看向心加速度
(1)直线运动
(2)圆周运动
(三)对向心加速度的理解
3、对向心加速度的理解
(1) 物理意义:描述匀速圆周运动中线速度改变的快慢,只能表示速度方向变化的快慢,不表示速度大小变化的快慢。
(2)方向特点
①指向圆心:无论是匀速圆周运动,还是变速圆周运动,向心加速度的方向都指向圆心(或者说与线速度方向垂直)。
②时刻改变:无论向心加速度的大小是否变化,向心加速度的方向随线速度方向的改变时刻改变,所以圆周运动的向心加速度是时刻改变的。
(3)“匀速圆周运动中的“变”与“不变”
① “不变”量:匀速圆周运动的角速度、周期、转速不变,线速度、加速度这两个矢量的大小不变。
②“变化”量:匀速圆周运动的线速度、加速度这两个矢量的方向时刻改变,故它们在时刻变化。
例题:如图 6.3-3 所示,在长为 l 的细绳下端拴一个质量 为 m 的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。 当绳子跟竖直方向的夹角为 θ 时,小球运动的向心加速 度 an 的大小为多少?通过计算说明 :要增大夹角 θ,应 该增大小球运动的角速度 ω。
三、向心加速度公式也适用于非匀速圆周运动.
1、变速圆周运动的向心加速度
做变速圆周运动的物体,加速度一般情况下不指向圆心,该加速度有两个分量:
一是向心加速度,
二是切向加速度.
(1)向心加速度表示速度方向变化的快慢,
(2)切向加速度表示速度大小变化的快慢.
所以变速圆周运动中,向心加速度的方向也总是指向圆心.对于变速圆周运动,如图所示,物体加速度的方向不再指向圆心,但其中一个分加速度的方向指向圆心,为向心加速度,仍满足公式an,其作用仍然是改变速度的方向。
(2)它们的线速度大小相等,在相同时间内甲与圆心的连线扫过的角度比乙的大。
(1)它们的角速度相等,乙的线速度小。
四、传动装置
课堂练习
