6.2向心力 课件 29张PPT
文档属性
| 名称 | 6.2向心力 课件 29张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 33.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-08 16:06:23 | ||
图片预览







文档简介
6.2 向心力
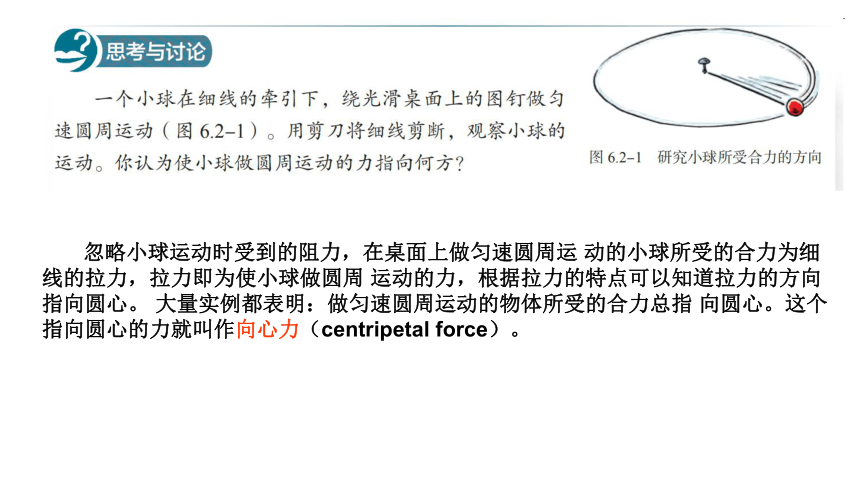
做圆周运动的物体,其运动状态在不断变化,说明物体一定受到了力的作用。那么迫使物体做圆周运动的力的 方向有何特点呢?
一、向心力
忽略小球运动时受到的阻力,在桌面上做匀速圆周运 动的小球所受的合力为细线的拉力,拉力即为使小球做圆周 运动的力,根据拉力的特点可以知道拉力的方向指向圆心。 大量实例都表明:做匀速圆周运动的物体所受的合力总指 向圆心。这个指向圆心的力就叫作向心力(centripetal force)。
(一)向心力的概念
1.向心力定义:做匀速圆周运动的物体所受的合力总指向圆心。这个指向圆心的力就叫作向心力。“向心力”一词是从这种合外力作用所产生的效果而命名的。
2.向心力的方向:无论是否为匀速圆周运动,其向心力总是沿着半径指向圆心,方向时刻改变,故向心力是变力.
3.作用效果:向心力只改变线速度的方向,不改变线速度的大小,由于向心力始终指向圆心,其方向与物体运动方向始终垂直,故向心力不改变线速度的大小.它不是具有特定性质的某种力,任何性质的力都可以作为向心力.质点做圆周运动时,任意时刻都有沿切线方向飞出的趋势,而向心力的作用正是使质点沿圆轨道运动,如果某一时刻失去向心力,质点从此时刻起就沿切线方向飞出去.
(二)向心力的来源(谁符合当向心力)
向心力是根据力的作用效果命名的.它可以由重力、弹力、摩擦力等各种性质的力提供,也可以由它们的合力提供,还可以由某个力的分力提供.例如,地球绕太阳的运动可近似看作匀速圆周运动,太阳对地球 的引力提供向心力 ;在本节的“问题”所说的空中飞椅项 目中,飞椅与人一起做圆周运动的向心力 Fn 则是由绳子斜 向上方的拉力 F 和所受重力 G 的合力提供的。
1、当物体做匀速圆周运动时,由于物体沿切线方向的加速度为零,即切线方向的合力为零,物体受到的合外力一定指向圆心,所以合力充当向心力。
2、当物体做非匀速圆周运动时,其向心力为物体所受的合外力在半径方向上的分力,而合外力在切线方向的分力则用于改变线速度的大小.
3、无论是匀速圆周运动还是非匀速圆周运动,物体所受各力沿半径方向分量的矢量和提供向心力.
二、向心力的大小
在物理学中,认识物理量时可以先定性了解,然后再 探究不同物理量之间的定量关系。因此,我们也先通过实验感受向心力大小与圆周运动的一些运动学量之间的定性关系,再通过实验,进一步探究向心力的大小与这些量的定量关系。
1、感受向心力
如图 6.2-3 所示,在绳子的一端拴一个小沙袋(或其他小物体),另一端握在手中。将手举过头顶,使沙 袋在水平面内做圆周运动。此时,沙袋所受的向心力近 似等于手通过绳对沙袋的拉力。换用不同质量的沙袋, 并改变沙袋转动的速度和绳的长度,感受向心力的变化。
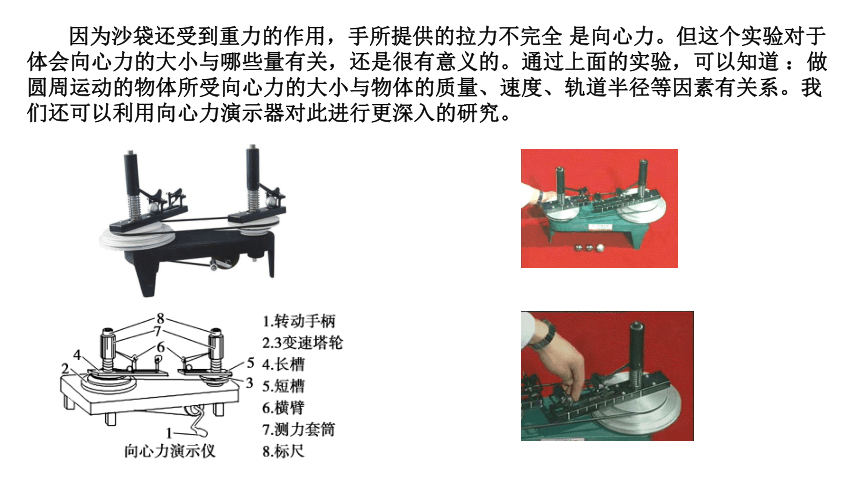
因为沙袋还受到重力的作用,手所提供的拉力不完全 是向心力。但这个实验对于体会向心力的大小与哪些量有关,还是很有意义的。通过上面的实验,可以知道 :做圆周运动的物体所受向心力的大小与物体的质量、速度、轨道半径等因素有关系。我们还可以利用向心力演示器对此进行更深入的研究。
2、探究向心力大小的表达式
(1)实验目的:探究做圆周运动的物体所需要的向心力F与其质量m、转运半径r和转动角速度ω之间的关系
(2)实验方法:控制变量法
(3)实验过程
①保持两个小球质量m和角速度ω相同,使两球运动半径r不同进行实验,比较向心力Fn与运动半径r之间的关系.
②保持两个小球质量m和运动半径r相同,使两球的角速度ω不同进行实验,比较向心力Fn与角速度ω之间的关系.
③保持运动半径r和角速度ω相同,用质量m不同的钢球和铝球进行实验,比较向心力Fn与质量m的关系.
①保持两个小球质量m和角速度ω相同,使两球运动半径r不同进行实验,比较向心力Fn与运动半径r之间的关系.
②保持两个小球质量m和运动半径r相同,使两球的角速度ω不同进行实验,比较向心力Fn与角速度ω之间的关系.
ω相同进行实验
ω不同进行实验
③保持运动半径r和角速度ω相同,用质量m不同的钢球和铝球进行实验,比较向心力Fn与质量m的关系.
三、变速圆周运动和一般曲线运动的受力特点
仔细观察运动员掷链球时的动作,结合手握绳子使沙 袋加速转动的体会,可以发现 :我们使沙袋加速转动时, 绳子牵引沙袋的方向并不与沙袋运动的方向垂直。也就是 说,沙袋加速时,它所受的力并不严格指向运动轨迹的圆心。
1、图 6.2-5 表示做圆周运动的沙袋正在加速转动的情况。 O 是沙袋运动轨迹的圆心,F 是绳对沙袋的拉力。根据 F 产生的效果,可以把 F 分解为两个相互垂直的分力:跟圆 周相切的分力 Ft 和指向圆心的分力 Fn。Ft 与沙袋运动的速 度同向,使得沙袋的速度越来越大 ;Fn 指向圆心,提供沙 袋做圆周运动所需的向心力,改变沙袋速度的方向。
变速圆周运动所受合外力一般不等于向心力,合外力一般产生两个方面的效果:
(1)合外力F 跟圆周相切的分力Ft,此分力与物体运动的速度在一条直线上来改变速度大小
(2)合外力F 指向圆心的分力Fn,此分力提供物体做圆周运动所需的向心力,改变物体速度的方向.
①合外力的方向与速度方向夹角小于90°,如图甲所示,其中Ft只改变v的大小,使速度增加,Fn产生向心加速度,改变速度方向.
②F与v夹角大于90°时,Ft使v减小,Fn改变速度方向,如图乙所示.
结论:同时具有向心加速度和切向加速度的圆周运动就是变速圆周运动 ,匀速圆周运动切向加速度为零。
2、运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。尽管这时曲线各个位置的弯曲程度不 一样,但在研究时,可以把这条曲线分割为许多很短的小 段,质点在每小段的运动都可以看作圆周运动的一部分(图 6.2-6)。这样,在分析质点经过曲线上某位置的运动时, 就可以采用圆周运动的分析方法来处理了。
3.圆周运动与曲线运动
(1)向心力公式Fn=mv2/r,其意义是:质量为m的物体,在半径为r的圆周上以速率v做匀速圆周运动,所需的向心力大小是mv2/r,
(2)向心力公式Fn=mω2r,其意义是:质量为m的物体在半径为r的圆周上以角速度ω做匀速圆周运动,所需的合外力是mω2r,如果物体所受的合外力大小不满足mv2/r或mω2r等,方向不总是垂直于线速度的方向,物体就会偏离圆轨道做一般的曲线运动.
1、(多选)下面关于向心力的叙述中,正确的是( )
A.向心力的方向始终沿着半径指向圆心,所以是一个变力
B.做匀速圆周运动的物体,除了受到别的物体对它的作用力外,还一定受到一个向心力的作用
C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力
D.向心力只改变物体速度的方向,不改变物体速度的大小
课堂练习
解析选:ACD [向心力是根据力的作用效果来命名的,它可以是物体受力的合力,也可以是某一个力的分力,因此,在进行受力分析时,不能再分析向心力.向心力时刻指向圆心,与速度方向垂直,所以向心力只改变速度方向,不改变速度大小,A、C、D正确.]
7、用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关.
(1)本实验采用的科学方法是 .
A.控制变量法 B.累积法
C.微元法 D.放大法
(2)图示情景正在探究的是 .
A.向心力的大小与半径的关系
B.向心力的大小与线速度大小的关系
C.向心力的大小与角速度大小的关系
D.向心力的大小与物体质量的关系
(3)通过本实验可以得到的结果是 .
A.在质量和半径一定的情况下,向心力的大小与角速度成正比
B.在质量和半径一定的情况下,向心力的大小与线速度的大小成正比
C.在半径和角速度一定的情况下,向心力的大小与质量成正比
D.在质量和角速度一定的情况下,向心力的大小与半径成正比
[解析]
(1)这个装置中,控制半径、角速度不变,只改变质量,来研究向心力与质量之间的关系,故采用控制变量法,A正确.
(2)控制半径、角速度不变,只改变质量,来研究向心力与质量之间的关系,所以选项D正确.
(3)通过控制变量法,得到的结果为在半径和角速度一定的情况下,向心力的大小与质量成正比,所以选项C正确.
[答案] (1)A (2)D (3)C
做圆周运动的物体,其运动状态在不断变化,说明物体一定受到了力的作用。那么迫使物体做圆周运动的力的 方向有何特点呢?
一、向心力
忽略小球运动时受到的阻力,在桌面上做匀速圆周运 动的小球所受的合力为细线的拉力,拉力即为使小球做圆周 运动的力,根据拉力的特点可以知道拉力的方向指向圆心。 大量实例都表明:做匀速圆周运动的物体所受的合力总指 向圆心。这个指向圆心的力就叫作向心力(centripetal force)。
(一)向心力的概念
1.向心力定义:做匀速圆周运动的物体所受的合力总指向圆心。这个指向圆心的力就叫作向心力。“向心力”一词是从这种合外力作用所产生的效果而命名的。
2.向心力的方向:无论是否为匀速圆周运动,其向心力总是沿着半径指向圆心,方向时刻改变,故向心力是变力.
3.作用效果:向心力只改变线速度的方向,不改变线速度的大小,由于向心力始终指向圆心,其方向与物体运动方向始终垂直,故向心力不改变线速度的大小.它不是具有特定性质的某种力,任何性质的力都可以作为向心力.质点做圆周运动时,任意时刻都有沿切线方向飞出的趋势,而向心力的作用正是使质点沿圆轨道运动,如果某一时刻失去向心力,质点从此时刻起就沿切线方向飞出去.
(二)向心力的来源(谁符合当向心力)
向心力是根据力的作用效果命名的.它可以由重力、弹力、摩擦力等各种性质的力提供,也可以由它们的合力提供,还可以由某个力的分力提供.例如,地球绕太阳的运动可近似看作匀速圆周运动,太阳对地球 的引力提供向心力 ;在本节的“问题”所说的空中飞椅项 目中,飞椅与人一起做圆周运动的向心力 Fn 则是由绳子斜 向上方的拉力 F 和所受重力 G 的合力提供的。
1、当物体做匀速圆周运动时,由于物体沿切线方向的加速度为零,即切线方向的合力为零,物体受到的合外力一定指向圆心,所以合力充当向心力。
2、当物体做非匀速圆周运动时,其向心力为物体所受的合外力在半径方向上的分力,而合外力在切线方向的分力则用于改变线速度的大小.
3、无论是匀速圆周运动还是非匀速圆周运动,物体所受各力沿半径方向分量的矢量和提供向心力.
二、向心力的大小
在物理学中,认识物理量时可以先定性了解,然后再 探究不同物理量之间的定量关系。因此,我们也先通过实验感受向心力大小与圆周运动的一些运动学量之间的定性关系,再通过实验,进一步探究向心力的大小与这些量的定量关系。
1、感受向心力
如图 6.2-3 所示,在绳子的一端拴一个小沙袋(或其他小物体),另一端握在手中。将手举过头顶,使沙 袋在水平面内做圆周运动。此时,沙袋所受的向心力近 似等于手通过绳对沙袋的拉力。换用不同质量的沙袋, 并改变沙袋转动的速度和绳的长度,感受向心力的变化。
因为沙袋还受到重力的作用,手所提供的拉力不完全 是向心力。但这个实验对于体会向心力的大小与哪些量有关,还是很有意义的。通过上面的实验,可以知道 :做圆周运动的物体所受向心力的大小与物体的质量、速度、轨道半径等因素有关系。我们还可以利用向心力演示器对此进行更深入的研究。
2、探究向心力大小的表达式
(1)实验目的:探究做圆周运动的物体所需要的向心力F与其质量m、转运半径r和转动角速度ω之间的关系
(2)实验方法:控制变量法
(3)实验过程
①保持两个小球质量m和角速度ω相同,使两球运动半径r不同进行实验,比较向心力Fn与运动半径r之间的关系.
②保持两个小球质量m和运动半径r相同,使两球的角速度ω不同进行实验,比较向心力Fn与角速度ω之间的关系.
③保持运动半径r和角速度ω相同,用质量m不同的钢球和铝球进行实验,比较向心力Fn与质量m的关系.
①保持两个小球质量m和角速度ω相同,使两球运动半径r不同进行实验,比较向心力Fn与运动半径r之间的关系.
②保持两个小球质量m和运动半径r相同,使两球的角速度ω不同进行实验,比较向心力Fn与角速度ω之间的关系.
ω相同进行实验
ω不同进行实验
③保持运动半径r和角速度ω相同,用质量m不同的钢球和铝球进行实验,比较向心力Fn与质量m的关系.
三、变速圆周运动和一般曲线运动的受力特点
仔细观察运动员掷链球时的动作,结合手握绳子使沙 袋加速转动的体会,可以发现 :我们使沙袋加速转动时, 绳子牵引沙袋的方向并不与沙袋运动的方向垂直。也就是 说,沙袋加速时,它所受的力并不严格指向运动轨迹的圆心。
1、图 6.2-5 表示做圆周运动的沙袋正在加速转动的情况。 O 是沙袋运动轨迹的圆心,F 是绳对沙袋的拉力。根据 F 产生的效果,可以把 F 分解为两个相互垂直的分力:跟圆 周相切的分力 Ft 和指向圆心的分力 Fn。Ft 与沙袋运动的速 度同向,使得沙袋的速度越来越大 ;Fn 指向圆心,提供沙 袋做圆周运动所需的向心力,改变沙袋速度的方向。
变速圆周运动所受合外力一般不等于向心力,合外力一般产生两个方面的效果:
(1)合外力F 跟圆周相切的分力Ft,此分力与物体运动的速度在一条直线上来改变速度大小
(2)合外力F 指向圆心的分力Fn,此分力提供物体做圆周运动所需的向心力,改变物体速度的方向.
①合外力的方向与速度方向夹角小于90°,如图甲所示,其中Ft只改变v的大小,使速度增加,Fn产生向心加速度,改变速度方向.
②F与v夹角大于90°时,Ft使v减小,Fn改变速度方向,如图乙所示.
结论:同时具有向心加速度和切向加速度的圆周运动就是变速圆周运动 ,匀速圆周运动切向加速度为零。
2、运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。尽管这时曲线各个位置的弯曲程度不 一样,但在研究时,可以把这条曲线分割为许多很短的小 段,质点在每小段的运动都可以看作圆周运动的一部分(图 6.2-6)。这样,在分析质点经过曲线上某位置的运动时, 就可以采用圆周运动的分析方法来处理了。
3.圆周运动与曲线运动
(1)向心力公式Fn=mv2/r,其意义是:质量为m的物体,在半径为r的圆周上以速率v做匀速圆周运动,所需的向心力大小是mv2/r,
(2)向心力公式Fn=mω2r,其意义是:质量为m的物体在半径为r的圆周上以角速度ω做匀速圆周运动,所需的合外力是mω2r,如果物体所受的合外力大小不满足mv2/r或mω2r等,方向不总是垂直于线速度的方向,物体就会偏离圆轨道做一般的曲线运动.
1、(多选)下面关于向心力的叙述中,正确的是( )
A.向心力的方向始终沿着半径指向圆心,所以是一个变力
B.做匀速圆周运动的物体,除了受到别的物体对它的作用力外,还一定受到一个向心力的作用
C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力
D.向心力只改变物体速度的方向,不改变物体速度的大小
课堂练习
解析选:ACD [向心力是根据力的作用效果来命名的,它可以是物体受力的合力,也可以是某一个力的分力,因此,在进行受力分析时,不能再分析向心力.向心力时刻指向圆心,与速度方向垂直,所以向心力只改变速度方向,不改变速度大小,A、C、D正确.]
7、用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关.
(1)本实验采用的科学方法是 .
A.控制变量法 B.累积法
C.微元法 D.放大法
(2)图示情景正在探究的是 .
A.向心力的大小与半径的关系
B.向心力的大小与线速度大小的关系
C.向心力的大小与角速度大小的关系
D.向心力的大小与物体质量的关系
(3)通过本实验可以得到的结果是 .
A.在质量和半径一定的情况下,向心力的大小与角速度成正比
B.在质量和半径一定的情况下,向心力的大小与线速度的大小成正比
C.在半径和角速度一定的情况下,向心力的大小与质量成正比
D.在质量和角速度一定的情况下,向心力的大小与半径成正比
[解析]
(1)这个装置中,控制半径、角速度不变,只改变质量,来研究向心力与质量之间的关系,故采用控制变量法,A正确.
(2)控制半径、角速度不变,只改变质量,来研究向心力与质量之间的关系,所以选项D正确.
(3)通过控制变量法,得到的结果为在半径和角速度一定的情况下,向心力的大小与质量成正比,所以选项C正确.
[答案] (1)A (2)D (3)C
