6.4生活中的圆周运动 课件 33张PPT
文档属性
| 名称 | 6.4生活中的圆周运动 课件 33张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 31.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览







文档简介
6.4 生活中的圆周运动
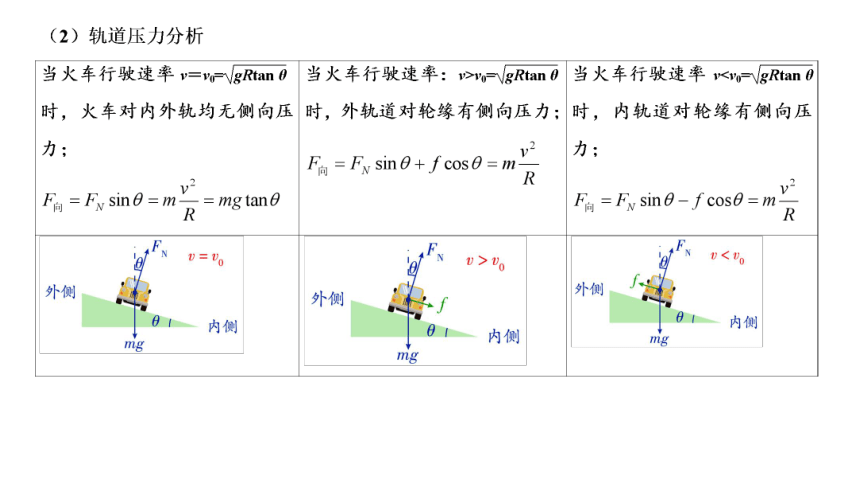
一、火车转弯
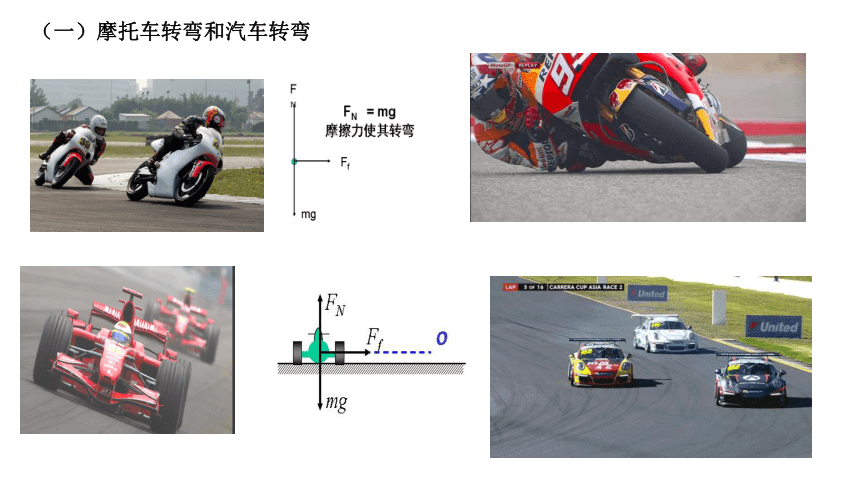
(一)摩托车转弯和汽车转弯
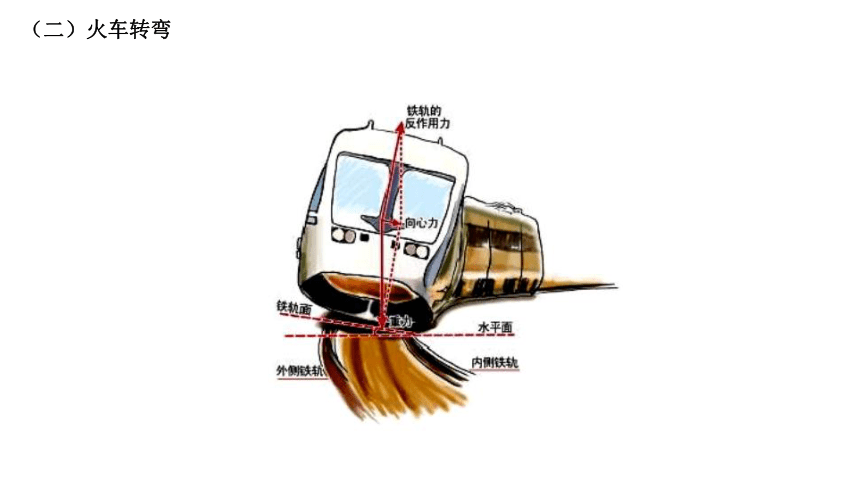
(二)火车转弯
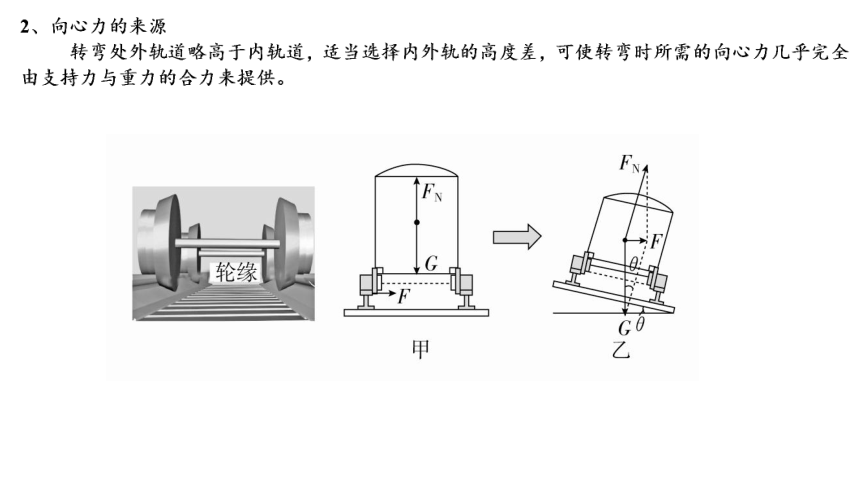
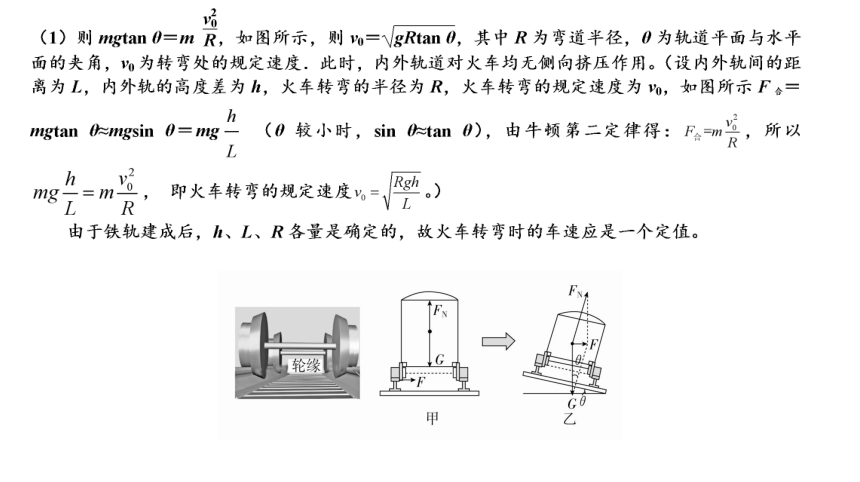
1、了解轮缘
二、汽车过拱形桥
(一)拱桥
汽车过拱形桥时的运动也可以看作圆周运动。质量为m 的汽车在拱形桥上以速度 v 前进,设桥面的圆弧半径为 r,我们来分析汽车通过桥的最高点时对桥的压力。
选汽车为研究对象。分析汽车所受的力(图 6.4-4),如果知道了桥对汽车的支持力 FN,桥所受的压力也就知道了。汽车在竖直方向受到重力 G 和桥的支持力 FN,它们的合力就是使汽车做圆周运动的向心力 F。鉴于向心加速度的方向是竖直向下的,故合力为F = G - F N
二、凹桥
公路在通过小型水库泄洪闸的下游时常常要修建凹形路面,也叫“过水路面”。汽车通过凹形路面的最低点时(图 6.4-5),车对地面的压力比汽车所受的重力大些还是小些?同学们可以仿照上面的方法自己进行分析。
1、凹形桥
2、秋千
三、航天器中的失重现象
上面“思考与讨论”中描述的场景其实已经实现了, 不过不是在汽车上,而是在航天器中。我们以绕地球做匀速圆周运动的宇宙飞船为例做些说明。当飞船距地面高度 为 100 ? 200 km 时,它的轨道半径近似等于地球半径 R, 航天员受到的地球引力近似等于他在地面受到的重力 mg。
四、离心运动
做圆周运动的物体,由于惯性,总有沿着切线方向飞 出去的倾向。但是物体没有飞出去,这是因为向心力在拉 着它,使它与圆心的距离保持不变。一旦向心力突然消失, 物体就会沿切线方向飞出去。 除了向心力突然消失这种情况外,在合力不足以提供所需的向心力时,物体虽然不会沿切线飞去,也会逐渐远
离圆心这里描述的运动叫作离心运动
五、竖直面内圆周运动的临界问题
一、绳球模型与圆桶(细线约束的小球在竖直面上的变速圆周运动)
1、“水流星”—绳球模型
2、过山车
二、杆球模型与管道 (轻杆约束小球在竖直面上的变速圆周运动)
1、杆球模型
2、管道
课堂练习
一、火车转弯
(一)摩托车转弯和汽车转弯
(二)火车转弯
1、了解轮缘
二、汽车过拱形桥
(一)拱桥
汽车过拱形桥时的运动也可以看作圆周运动。质量为m 的汽车在拱形桥上以速度 v 前进,设桥面的圆弧半径为 r,我们来分析汽车通过桥的最高点时对桥的压力。
选汽车为研究对象。分析汽车所受的力(图 6.4-4),如果知道了桥对汽车的支持力 FN,桥所受的压力也就知道了。汽车在竖直方向受到重力 G 和桥的支持力 FN,它们的合力就是使汽车做圆周运动的向心力 F。鉴于向心加速度的方向是竖直向下的,故合力为F = G - F N
二、凹桥
公路在通过小型水库泄洪闸的下游时常常要修建凹形路面,也叫“过水路面”。汽车通过凹形路面的最低点时(图 6.4-5),车对地面的压力比汽车所受的重力大些还是小些?同学们可以仿照上面的方法自己进行分析。
1、凹形桥
2、秋千
三、航天器中的失重现象
上面“思考与讨论”中描述的场景其实已经实现了, 不过不是在汽车上,而是在航天器中。我们以绕地球做匀速圆周运动的宇宙飞船为例做些说明。当飞船距地面高度 为 100 ? 200 km 时,它的轨道半径近似等于地球半径 R, 航天员受到的地球引力近似等于他在地面受到的重力 mg。
四、离心运动
做圆周运动的物体,由于惯性,总有沿着切线方向飞 出去的倾向。但是物体没有飞出去,这是因为向心力在拉 着它,使它与圆心的距离保持不变。一旦向心力突然消失, 物体就会沿切线方向飞出去。 除了向心力突然消失这种情况外,在合力不足以提供所需的向心力时,物体虽然不会沿切线飞去,也会逐渐远
离圆心这里描述的运动叫作离心运动
五、竖直面内圆周运动的临界问题
一、绳球模型与圆桶(细线约束的小球在竖直面上的变速圆周运动)
1、“水流星”—绳球模型
2、过山车
二、杆球模型与管道 (轻杆约束小球在竖直面上的变速圆周运动)
1、杆球模型
2、管道
课堂练习
