5.4 抛体运动 3-平抛运动与斜面相结合的问题 学案Word版含答案
文档属性
| 名称 | 5.4 抛体运动 3-平抛运动与斜面相结合的问题 学案Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-08 16:21:59 | ||
图片预览

文档简介
5-3
抛体运动
3-平抛运动与斜面相结合的问题
【知识点梳理】
1、常见的有两类情况
(1)物体从斜面上某一点水平抛出以后又重新落在斜面上,此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角.
(2)做平抛运动的物体垂直打在斜面上,此时物体的合速度与竖直方向的夹角等于斜面的倾角.
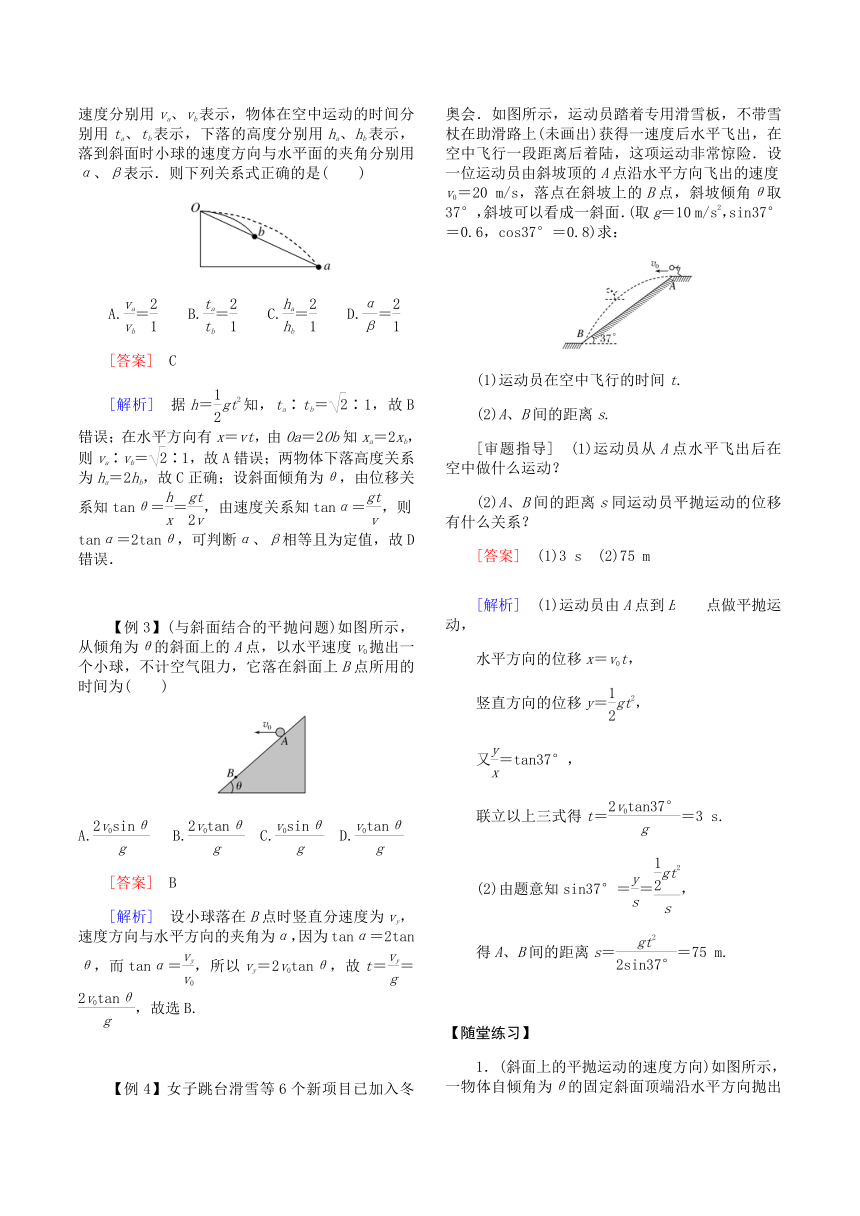
2、两类与斜面结合的平抛运动
(1)从斜面上开始运动又落在斜面上
速度方向与斜面夹角恒定;运动时间t=.
(2)垂直打在斜面上
速度方向与斜面垂直;运动时间t=.
实例
实例1
实例2
图示
定量
关系
tanθ==
tanθ==
3.求解方法
(1)对于重新落在斜面上的平抛运动,画出位移分解图;对于垂直打在斜面上的平抛运动,画出速度分解图.
(2)确定合速度(或合位移)与水平方向的夹角,利用夹角确定分速度(或分位移)的关系tanθ=
.
(3)再结合平抛运动在水平方向和竖直方向的位移公式或速度公式列式求解.
【例题讲解】
【例1】如图所示,从倾角为θ的斜面上某点先后将同一小球以不同的初速度水平抛出,小球均落在斜面上.当抛出的速度为v1时,小球落在斜面上时速度方向与斜面的夹角为α1;当抛出速度为v2时,小球落在斜面上时速度方向与斜面的夹角为α2,则( )
A.当v1>v2时,α1>α2
B.当v1>v2时,α1<α2
C.无论v1、v2关系如何,均有α1=α2
D.α1、α2的关系与斜面倾角θ有关
[答案] C
[解析] 小球从斜面上某点抛出后落到斜面上,小球的位移与水平方向的夹角等于斜面的倾角θ,即tanθ===,小球落到斜面上时速度方向与水平方向的夹角的正切值tanφ==,故可得tanφ=2tanθ.只要小球落到斜面上,位移方向与水平方向的夹角就总是θ,则小球的速度方向与水平方向的夹角也总是φ,故速度方向与斜面的夹角总是相等,与v1、v2的关系无关,C选项正确.
【例2】如图所示,某人先后两次由斜面体顶端的O点沿水平方向抛出两个可视为质点的物体,第一次的落地点为斜面体上的a点,第二次的落地点为斜面体上的b点,且Oa=2Ob,两次物体的初速度分别用va、vb表示,物体在空中运动的时间分别用ta、tb表示,下落的高度分别用ha、hb表示,落到斜面时小球的速度方向与水平面的夹角分别用α、β表示.则下列关系式正确的是( )
A.=
B.=
C.=
D.=
[答案] C
[解析] 据h=gt2知,ta∶tb=∶1,故B错误;在水平方向有x=vt,由Oa=2Ob知xa=2xb,则va∶vb=∶1,故A错误;两物体下落高度关系为ha=2hb,故C正确;设斜面倾角为θ,由位移关系知tanθ==,由速度关系知tanα=,则tanα=2tanθ,可判断α、β相等且为定值,故D错误.
【例3】(与斜面结合的平抛问题)如图所示,从倾角为θ的斜面上的A点,以水平速度v0抛出一个小球,不计空气阻力,它落在斜面上B点所用的时间为( )
A.
B.
C.
D.
[答案] B
[解析] 设小球落在B点时竖直分速度为vy,速度方向与水平方向的夹角为α,因为tanα=2tanθ,而tanα=,所以vy=2v0tanθ,故t==,故选B.
【例4】女子跳台滑雪等6个新项目已加入冬奥会.如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(未画出)获得一速度后水平飞出,在空中飞行一段距离后着陆,这项运动非常惊险.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20
m/s,落点在斜坡上的B点,斜坡倾角θ取37°,斜坡可以看成一斜面.(取g=10
m/s2,sin37°=0.6,cos37°=0.8)求:
(1)运动员在空中飞行的时间t.
(2)A、B间的距离s.
[审题指导] (1)运动员从A点水平飞出后在空中做什么运动?
(2)A、B间的距离s同运动员平抛运动的位移有什么关系?
[答案] (1)3
s (2)75
m
[解析] (1)运动员由A点到B点做平抛运动,
水平方向的位移x=v0t,
竖直方向的位移y=gt2,
又=tan37°,
联立以上三式得t==3
s.
(2)由题意知sin37°==,
得A、B间的距离s==75
m.
【随堂练习】
1.(斜面上的平抛运动的速度方向)如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上.物体与斜面接触时速度与水平方向的夹角φ满足( )
A.tanφ=sinθ
B.tanφ=cosθ
C.tanφ=tanθ
D.tanφ=2tanθ
[答案] D
[解析] 设物体飞行时间为t,则tanφ==,tanθ===,故tanφ=2tanθ,D正确.故选D.
2.(斜面上的平抛运动的运动时间)如图所示,同样高度的两个斜面,倾角分别为37°和53°,在顶点两个小球A,B以同样大小的初速度v0分别向左、向右水平抛出,小球都落在斜面上,若不计空气阻力,则A,B两个小球运动时间之比为( )
A.1∶1
B.4∶3
C.16∶9
D.9∶16
[答案] D
[解析] 结合平抛运动知识,A球满足tan37°=,B球满足tan53°=,则t1∶t2=9∶16.故D选项正确.
【课后作业】
1.如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角为α,若把小球初速度变为原来的倍,则下列说法正确的是( )
A.小球在空中运动时间变为原来的2倍
B.落在斜面上的速度方向与斜面间的夹角大于α
C.抛出点到落到斜面上的点的距离一定等于PQ的4倍
D.落在斜面上的速度方向与斜面间的夹角等于α
[解析] 由tanθ===可知,小球在空中运动时间变为原来的倍,抛出点到落到斜面上的点的距离为PQ的2倍,水平速度与竖直速度的比值不变,故合速度方向不变,可得落在斜面上的速度方向与斜面间的夹角等于α,故D正确,A、B、C错误.
[答案] D
2.一水平抛出的小球落到一倾角为θ的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示.小球在竖直方向下落的距离与在水平方向通过的距离之比为( )
A.tanθ
B.2tanθ
C.
D.
[解析] 设小球的初速度为v0,抛出t时间后小球落在斜面上.根据速度方向与斜面垂直,求得t时小球的竖直速度vy=,故时间t==.t时间内小球水平位移x=v0t=,竖直位移y==,=,选项D正确.
[答案] D
3.(多选)如图所示,在某次自由式滑雪比赛中,一运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )
A.如果v0不同,则该运动员落到雪坡时的速度方向也就不同
B.不论v0多大,该运动员落到雪坡时的速度方向都是相同的
C.运动员落到雪坡时的速度大小是
D.运动员在空中经历的时间是
[解析] 如果v0不同,则该运动员落到雪坡时的位置不同,但位移方向均沿斜坡,即位移方向与水平方向的夹角均为θ,设落到雪坡时速度方向与水平方向的夹角为φ,则tanφ=2tanθ,得速度方向与水平方向的夹角均为φ,故A错误,B正确;将运动员落到雪坡时的速度沿水平和竖直方向分解,求出运动员落到雪坡时的速度大小为,故C错误;由几何关系得tanθ=,解出运动员在空中经历的时间t=,故D正确.
[答案] BD
抛体运动
3-平抛运动与斜面相结合的问题
【知识点梳理】
1、常见的有两类情况
(1)物体从斜面上某一点水平抛出以后又重新落在斜面上,此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角.
(2)做平抛运动的物体垂直打在斜面上,此时物体的合速度与竖直方向的夹角等于斜面的倾角.
2、两类与斜面结合的平抛运动
(1)从斜面上开始运动又落在斜面上
速度方向与斜面夹角恒定;运动时间t=.
(2)垂直打在斜面上
速度方向与斜面垂直;运动时间t=.
实例
实例1
实例2
图示
定量
关系
tanθ==
tanθ==
3.求解方法
(1)对于重新落在斜面上的平抛运动,画出位移分解图;对于垂直打在斜面上的平抛运动,画出速度分解图.
(2)确定合速度(或合位移)与水平方向的夹角,利用夹角确定分速度(或分位移)的关系tanθ=
.
(3)再结合平抛运动在水平方向和竖直方向的位移公式或速度公式列式求解.
【例题讲解】
【例1】如图所示,从倾角为θ的斜面上某点先后将同一小球以不同的初速度水平抛出,小球均落在斜面上.当抛出的速度为v1时,小球落在斜面上时速度方向与斜面的夹角为α1;当抛出速度为v2时,小球落在斜面上时速度方向与斜面的夹角为α2,则( )
A.当v1>v2时,α1>α2
B.当v1>v2时,α1<α2
C.无论v1、v2关系如何,均有α1=α2
D.α1、α2的关系与斜面倾角θ有关
[答案] C
[解析] 小球从斜面上某点抛出后落到斜面上,小球的位移与水平方向的夹角等于斜面的倾角θ,即tanθ===,小球落到斜面上时速度方向与水平方向的夹角的正切值tanφ==,故可得tanφ=2tanθ.只要小球落到斜面上,位移方向与水平方向的夹角就总是θ,则小球的速度方向与水平方向的夹角也总是φ,故速度方向与斜面的夹角总是相等,与v1、v2的关系无关,C选项正确.
【例2】如图所示,某人先后两次由斜面体顶端的O点沿水平方向抛出两个可视为质点的物体,第一次的落地点为斜面体上的a点,第二次的落地点为斜面体上的b点,且Oa=2Ob,两次物体的初速度分别用va、vb表示,物体在空中运动的时间分别用ta、tb表示,下落的高度分别用ha、hb表示,落到斜面时小球的速度方向与水平面的夹角分别用α、β表示.则下列关系式正确的是( )
A.=
B.=
C.=
D.=
[答案] C
[解析] 据h=gt2知,ta∶tb=∶1,故B错误;在水平方向有x=vt,由Oa=2Ob知xa=2xb,则va∶vb=∶1,故A错误;两物体下落高度关系为ha=2hb,故C正确;设斜面倾角为θ,由位移关系知tanθ==,由速度关系知tanα=,则tanα=2tanθ,可判断α、β相等且为定值,故D错误.
【例3】(与斜面结合的平抛问题)如图所示,从倾角为θ的斜面上的A点,以水平速度v0抛出一个小球,不计空气阻力,它落在斜面上B点所用的时间为( )
A.
B.
C.
D.
[答案] B
[解析] 设小球落在B点时竖直分速度为vy,速度方向与水平方向的夹角为α,因为tanα=2tanθ,而tanα=,所以vy=2v0tanθ,故t==,故选B.
【例4】女子跳台滑雪等6个新项目已加入冬奥会.如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(未画出)获得一速度后水平飞出,在空中飞行一段距离后着陆,这项运动非常惊险.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20
m/s,落点在斜坡上的B点,斜坡倾角θ取37°,斜坡可以看成一斜面.(取g=10
m/s2,sin37°=0.6,cos37°=0.8)求:
(1)运动员在空中飞行的时间t.
(2)A、B间的距离s.
[审题指导] (1)运动员从A点水平飞出后在空中做什么运动?
(2)A、B间的距离s同运动员平抛运动的位移有什么关系?
[答案] (1)3
s (2)75
m
[解析] (1)运动员由A点到B点做平抛运动,
水平方向的位移x=v0t,
竖直方向的位移y=gt2,
又=tan37°,
联立以上三式得t==3
s.
(2)由题意知sin37°==,
得A、B间的距离s==75
m.
【随堂练习】
1.(斜面上的平抛运动的速度方向)如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上.物体与斜面接触时速度与水平方向的夹角φ满足( )
A.tanφ=sinθ
B.tanφ=cosθ
C.tanφ=tanθ
D.tanφ=2tanθ
[答案] D
[解析] 设物体飞行时间为t,则tanφ==,tanθ===,故tanφ=2tanθ,D正确.故选D.
2.(斜面上的平抛运动的运动时间)如图所示,同样高度的两个斜面,倾角分别为37°和53°,在顶点两个小球A,B以同样大小的初速度v0分别向左、向右水平抛出,小球都落在斜面上,若不计空气阻力,则A,B两个小球运动时间之比为( )
A.1∶1
B.4∶3
C.16∶9
D.9∶16
[答案] D
[解析] 结合平抛运动知识,A球满足tan37°=,B球满足tan53°=,则t1∶t2=9∶16.故D选项正确.
【课后作业】
1.如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角为α,若把小球初速度变为原来的倍,则下列说法正确的是( )
A.小球在空中运动时间变为原来的2倍
B.落在斜面上的速度方向与斜面间的夹角大于α
C.抛出点到落到斜面上的点的距离一定等于PQ的4倍
D.落在斜面上的速度方向与斜面间的夹角等于α
[解析] 由tanθ===可知,小球在空中运动时间变为原来的倍,抛出点到落到斜面上的点的距离为PQ的2倍,水平速度与竖直速度的比值不变,故合速度方向不变,可得落在斜面上的速度方向与斜面间的夹角等于α,故D正确,A、B、C错误.
[答案] D
2.一水平抛出的小球落到一倾角为θ的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示.小球在竖直方向下落的距离与在水平方向通过的距离之比为( )
A.tanθ
B.2tanθ
C.
D.
[解析] 设小球的初速度为v0,抛出t时间后小球落在斜面上.根据速度方向与斜面垂直,求得t时小球的竖直速度vy=,故时间t==.t时间内小球水平位移x=v0t=,竖直位移y==,=,选项D正确.
[答案] D
3.(多选)如图所示,在某次自由式滑雪比赛中,一运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )
A.如果v0不同,则该运动员落到雪坡时的速度方向也就不同
B.不论v0多大,该运动员落到雪坡时的速度方向都是相同的
C.运动员落到雪坡时的速度大小是
D.运动员在空中经历的时间是
[解析] 如果v0不同,则该运动员落到雪坡时的位置不同,但位移方向均沿斜坡,即位移方向与水平方向的夹角均为θ,设落到雪坡时速度方向与水平方向的夹角为φ,则tanφ=2tanθ,得速度方向与水平方向的夹角均为φ,故A错误,B正确;将运动员落到雪坡时的速度沿水平和竖直方向分解,求出运动员落到雪坡时的速度大小为,故C错误;由几何关系得tanθ=,解出运动员在空中经历的时间t=,故D正确.
[答案] BD
