七年级数学平行线的性质第一课时课件
文档属性
| 名称 | 七年级数学平行线的性质第一课时课件 |  | |
| 格式 | zip | ||
| 文件大小 | 41.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-16 18:55:24 | ||
图片预览








文档简介
(共22张PPT)
平行线的性质
第一课时
教学目标:
1、理解并掌握平行线的三个性质,并能运用它们作简单的推理。
2、经历探索直线平行的性质的过程,并能灵活运用它们进行简单的推理和计算。
教学重点:
探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
教学难点:
能区分平行线的性质和判定,平行线的性质与判定的混合应用.
思考:
判定两条直线平行的三种条件是什么?
C
D
A
B
E
F
8
5
6
1
2
3
4
7
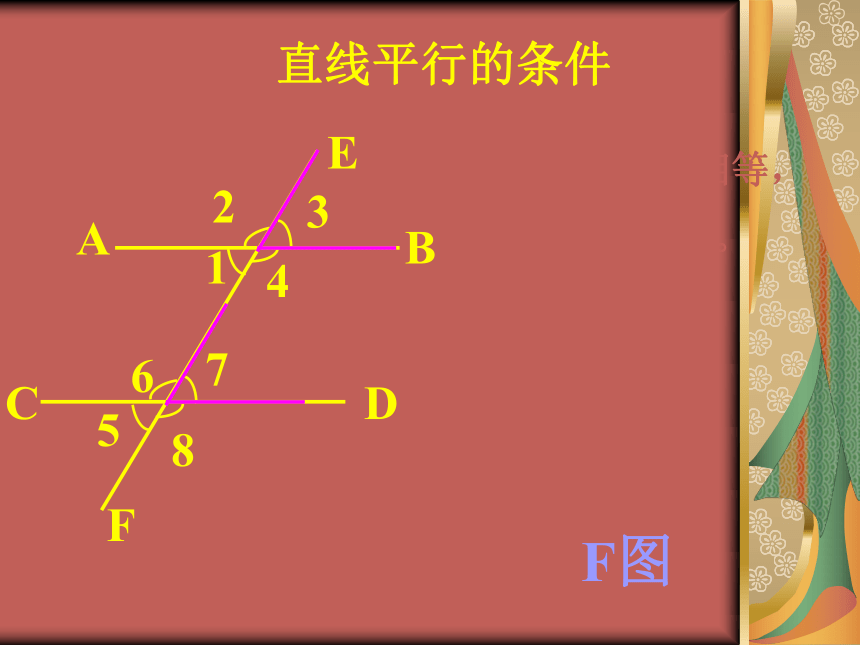
直线平行的条件
1、同位角相等,
两直线平行。
F图
探究新知
学生画图活动:用直尺和三角尺画出两条平行线a∥b,再画一条截线c与直线a、b相交,标出所形成的4个角
学生测量这些角的度数,并写出来.
∠1 ∠2 ∠ 3 ∠4度数分别是多少?
学生根据测量所得数据作出猜想.
图中哪些角是同位角 它们具有怎样的数量关系
图中哪些角是内错角 它们具有怎样的数量关系
图中哪些角是同旁内角 它们具有怎样的数量关系
归纳:
平行线的性质:
性质1:两条平行线被第三条直线所截,同位角相等,简称为两直线平行, 同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等,简称为两直线平行, 内错相等.
性质3:两条直线按被第三条线所截,同旁内角互补,简称为两直线平行, 同旁内角互补.
教师引导学生理清平行线的性质与平行线判定的区别.
平行线的性质 平行线的判定
因为a∥b, 因为∠1=∠2,
所以∠1=∠2 所以a∥b.
因为a∥b, 因为∠2=∠3,
所以∠2=∠3, 所以a∥b.
因为a∥b, 因为∠2+∠4=180°,
所以∠2+∠4=180°, 所以a∥b.
平行线性质应用.
例 (课本P23)如图是一块梯形铁片的线全部分,量得∠A=100°,∠B=115°, 梯形另外两个角分别是多少度
“直线平行的条件”与“平行线的性质”
条件
性质
1、同位角相等,
两直线平行
1、两直线平行,
同位角相等
2、内错角相等,
两直线平行
2、两直线平行,
内错角相等
3、同旁内角互补,
两直线平行
3、两直线平行,
同旁内角互补
类比
直线平行的
条件
平行线的
性质
由角的大小关系转化为直线的位置关系
由直线的位置关系转化为角的大小关系
巩固练习
1.如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
求证:∠1+∠2=90°.
2.如图所示,已知:∠1=∠2,
求证:∠3+∠4=180°.
课内总结
今天,你收获了什么?
课后作业
判断题.
1.两条直线被第三条直线所截,则同旁内角互补.( )
2.两条直线被第三条直线所截,如果同旁内角互补,那么同位角相等.( )
3.两条平行线被第三条直线所截,则一对同旁内角的平分线互相平行.( )
选择题.
1.∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2; C.∠1<∠2 D.无法确定
2.一个人驱车前进时,两次拐弯后,按原来的相反方向前进, 这两次拐弯的角度是( )
A.向右拐85°,再向右拐95°; B.向右拐85°,再向左拐85°
C.向右拐85°,再向右拐85°; D.向右拐85°,再向左拐95°
解答题
1.如图,已知:∠1=110°,∠2=110°,∠3=70°,求∠4的度数.
2.如图,已知:DE∥CB,∠1=∠2,求证:CD平分∠ECB.
平行线的性质
第一课时
教学目标:
1、理解并掌握平行线的三个性质,并能运用它们作简单的推理。
2、经历探索直线平行的性质的过程,并能灵活运用它们进行简单的推理和计算。
教学重点:
探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
教学难点:
能区分平行线的性质和判定,平行线的性质与判定的混合应用.
思考:
判定两条直线平行的三种条件是什么?
C
D
A
B
E
F
8
5
6
1
2
3
4
7
直线平行的条件
1、同位角相等,
两直线平行。
F图
探究新知
学生画图活动:用直尺和三角尺画出两条平行线a∥b,再画一条截线c与直线a、b相交,标出所形成的4个角
学生测量这些角的度数,并写出来.
∠1 ∠2 ∠ 3 ∠4度数分别是多少?
学生根据测量所得数据作出猜想.
图中哪些角是同位角 它们具有怎样的数量关系
图中哪些角是内错角 它们具有怎样的数量关系
图中哪些角是同旁内角 它们具有怎样的数量关系
归纳:
平行线的性质:
性质1:两条平行线被第三条直线所截,同位角相等,简称为两直线平行, 同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等,简称为两直线平行, 内错相等.
性质3:两条直线按被第三条线所截,同旁内角互补,简称为两直线平行, 同旁内角互补.
教师引导学生理清平行线的性质与平行线判定的区别.
平行线的性质 平行线的判定
因为a∥b, 因为∠1=∠2,
所以∠1=∠2 所以a∥b.
因为a∥b, 因为∠2=∠3,
所以∠2=∠3, 所以a∥b.
因为a∥b, 因为∠2+∠4=180°,
所以∠2+∠4=180°, 所以a∥b.
平行线性质应用.
例 (课本P23)如图是一块梯形铁片的线全部分,量得∠A=100°,∠B=115°, 梯形另外两个角分别是多少度
“直线平行的条件”与“平行线的性质”
条件
性质
1、同位角相等,
两直线平行
1、两直线平行,
同位角相等
2、内错角相等,
两直线平行
2、两直线平行,
内错角相等
3、同旁内角互补,
两直线平行
3、两直线平行,
同旁内角互补
类比
直线平行的
条件
平行线的
性质
由角的大小关系转化为直线的位置关系
由直线的位置关系转化为角的大小关系
巩固练习
1.如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
求证:∠1+∠2=90°.
2.如图所示,已知:∠1=∠2,
求证:∠3+∠4=180°.
课内总结
今天,你收获了什么?
课后作业
判断题.
1.两条直线被第三条直线所截,则同旁内角互补.( )
2.两条直线被第三条直线所截,如果同旁内角互补,那么同位角相等.( )
3.两条平行线被第三条直线所截,则一对同旁内角的平分线互相平行.( )
选择题.
1.∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2; C.∠1<∠2 D.无法确定
2.一个人驱车前进时,两次拐弯后,按原来的相反方向前进, 这两次拐弯的角度是( )
A.向右拐85°,再向右拐95°; B.向右拐85°,再向左拐85°
C.向右拐85°,再向右拐85°; D.向右拐85°,再向左拐95°
解答题
1.如图,已知:∠1=110°,∠2=110°,∠3=70°,求∠4的度数.
2.如图,已知:DE∥CB,∠1=∠2,求证:CD平分∠ECB.
