第25章解直角三角形单元教案
图片预览




文档简介
第二十五章 解直角三角形
单元教学计划
本单元的主要内容是直角三角形的边角关系及其实际应用。教材先从测量入手,给学生创设学习情景,接着研究直角三角形的边角关系——锐角三角形函数,最后运用勾股定理及锐角三角函数等知识解决一些简单的实际问题。
教学目标:
1.经历由情境引出问题,探索掌握有关的数学知识内容,再运用于实践的过程,培养学数学、用数学的意识与能力。
2.通过实例认识直角三角形的边角关系,即锐角三角函数(sinA,cosA,tanA,cotA);知道30、45、60角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角。
3.运用三角函数解决与直角三角形有关的简单的实际问题。
4.能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题。
课时安排:本章教学时间约需14课时。具体分配如下:
25.1 测量 1课时
25.2 锐角三角函数 3课时
25.3 解直角三角形 4课时
复习 2课时
单元测验与评讲 4课时
第二十五章 解直角三角形
25.1 测 量
教学目标:
本节主要研究如何利用已学知识尤其是相似三角形的相关知识解决生活中某些测量问题。
教学重点:探究和解决生活中的某些测量问题。
教学难点:探究解决生活中的某些测量问题的方法。
教学方法;探究法
教具准备:皮尺、测角仪
教学过程:
一.问题引入
1.测量操场旗杆有多高?
如图25.1.1,站在操场上,请你的同学量出你在太阳下的影子长度、旗杆的影子长度,再根据你的身高,便可以计算出旗杆的高度.
图25.1.1
2.如果就你一个人,又遇上阴天,那怎么办呢?人们想到了一种可行的方法,还是利用相似三角形的知识.
二.试一试
如图25.1.2所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.现在请你按1∶500的比例将△ABC画在纸上,并记为△A′B′C′,用刻度直尺量出纸上B′C′的长度,便可以算出旗杆的实际高度.
你知道计算的方法吗?(请你量一量、算一算。)
实际上,我们利用图25.1.2(1)中已知的数据就可以直接计算旗杆的高度,而这一问题的解决将涉及到直角三角形中的边角关系.直角三角形中,三条边有什么关系?它的边与角又有什么关系?这一切都是本章要探究的内容.
三.课堂练习
1.在一次数学活动课上,老师让同学们到操场测量旗杆的高度,然后回来交流各自的测量方法。小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图所示),然后沿BC方向走到D处,这时目测旗杆顶部A到竹竿顶部E处恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高。
你认为这种测量方法是否可行?请说明理由。
2.请你与你的同学一起设计两种方案,测量你们学校楼房的高度。
四.归纳小结:
两种测量的方法:
方法一:构造可以测量的与原三角形相似的小三角形,利用对应线段成比例的性质计算出所求线段的长;
方法二:利用比例尺在纸上画一个与实物三角形相似的小三角形,通过直尺测量出所求线段在纸上的长度,再利用比例尺计算出实际长度。
五.课后作业
P87 习题25.1
六.教学反思:
25.2锐角三角函数
1 锐角三角函数
教学目标:
1.了解锐角三角函数的定义;
2.初步掌握三角函数的性质;
3.知道几种特殊角的三角函数值;
4.掌握定理:在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半。
教学重点:掌握几种特殊角的三角函数值和定理“在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半”。
教学难点:掌握三角函数的性质
教学方法:探究法
教具准备:直尺、电脑、实物投影
教学过程
一.复习引入
1.已知Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,问两个三角形的三组边是否成比例?
2.观察图25.2.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3中,
=__________=__________
=__________=__________
(可以使用几何画板演示)
结论:当Rt△ABC中,∠A的大小不变时,三条边的比例也不变(即为一个固定值)。
二.讲述新课
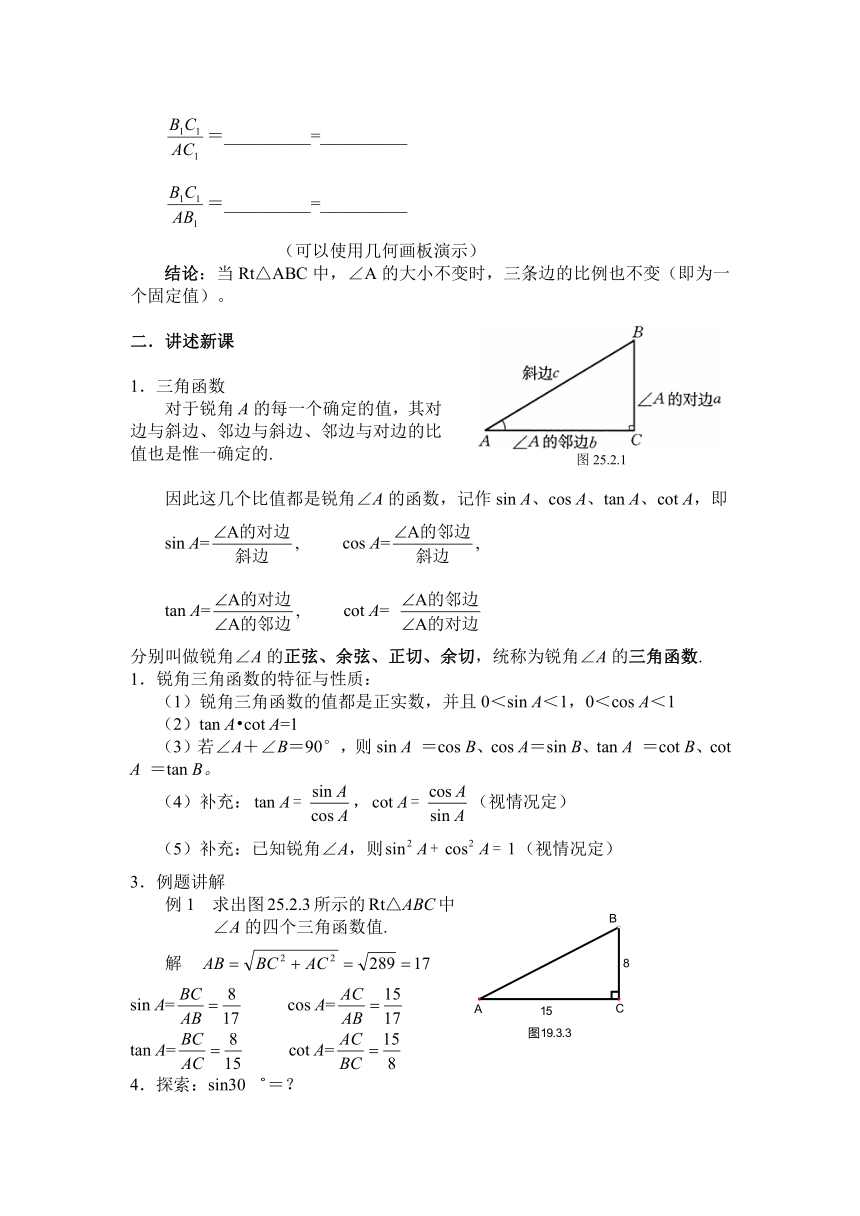
1.三角函数
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的.
因此这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A、cot A,即
sin A=, cos A=,
tan A=, cot A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
锐角三角函数的特征与性质:
(1)锐角三角函数的值都是正实数,并且0<sin A<1,0<cos A<1
(2)tan A cot A=1
(3)若∠A+∠B=90°,则sin A =cos B、cos A=sin B、tan A =cot B、cot A =tan B。
(4)补充:,(视情况定)
(5)补充:已知锐角∠A,则(视情况定)
3.例题讲解
求出图25.2.3所示的Rt△ABC中∠A的四个三角函数值.
解
sin A= cos A=
tan A= cot A=
4.探索:sin30゜=?
5.定理:在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半.
6.做一做:请填出空白处的值
三.课堂练习
P91(练习):1~4
四.归纳小结:
五.课后作业
P93(习题25.2):1~3
六.教学反思:
25.2锐角三角函数
用计算器求锐角三角函数值
教学目标:
1.会使用计算器求锐角三角函数的值;
2.会使用计算器根据锐角三角函数的值求对应的锐角。
教学重点:会使用计算器求锐角三角函数的值
教学难点:会使用计算器根据锐角三角函数的值求对应的锐角
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.讲述新课
1.如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角.
求已知锐角的三角函数值.
求sin63゜52′41″的值.(精确到0.0001)
解 先用如下方法将角度单位状态设定为“度”:
显示
再按下列顺序依次按键:
显示结果为0.897 859 012.
所以 sin63゜52′41″≈0.8979
例3 求cot70゜45′的值.(精确到0.0001)
解 在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序依次按键:
显示结果为0.349 215 633.
所以 cot70゜45′≈0.3492.
由锐角三角函数值求锐角
例4 已知tan x=0.7410,求锐角x.(精确到1′)
解 在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序
依次按键:
显示结果为36.538 445 77.
再按键:显示结果为36゜32′18.4.
所以,x≈36゜32′.
已知cot x=0.1950,求锐角x.(精确到1′)
分析 根据tan x=,可以求出tan x的值,然后根据例4的方法就可
以求出锐角x的值.
二.课堂练习
P93(练习):1~2
三.归纳小结:
四.作业:
P93(习题25.2):4~5
五.教学反思:
25.3 解直角三角形(1)
教学目标:
1.会运用三角函数解决与直角三角形有关的简单实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:
会运用三角函数解决与直角三角形有关的简单实际问题
教学难点:
会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:
探究法
教具准备:计算器、电脑、实物投影
教学过程
一.复习提问
复述勾股定理的内容:直角三角形两直角边的平方和等于斜边的平方.
锐角三角函数的定义:sin A=, cos A=,
tan A=, cot A= 。
锐角三角函数的特征与性质:
(1)锐角三角函数的值都是正实数,并且0<sin A<1,0<cos A<1
(2)tan A cot A=1
(3)若∠A+∠B=90°,则sin A =cos B、cos A=sin B、tan A =cot B、cot A =tan B。
(4)补充:,(视情况定)
(5)补充:已知锐角∠A,则(视情况定)
二.讲述新课
1.解直角三角形:在直角三角形中,除一个直角外,还有2个角和3条边共5个元素,由已知元素求出未知元素的过程,叫做解直角三角形。
2.例题讲解
例1: 在Rt△ABC中,∠C=90゜,已知,,解直角三角形。
分析:先根据条件画出三角形,可由勾股定理求出c,再由三角函数求锐角的度数。
[答案:,∠A=60°,∠B=30°]
例2(P93例1) 如图25.3.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
分析: 利用勾股定理求出折断倒下部分的长度,再求大树在折断前的高度。
[答案:36米]
三.归纳小结:
1.解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
2.在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.
四.课堂练习
P95练习第1题
五.课后作业:
P98习题25.3第1题
六.教学反思:
25.3 解直角三角形(2)
教学目标:
1.会运用三角函数解决与直角三角形有关的简单实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:会运用三角函数解决与直角三角形有关的简单实际问题
教学难点:会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.复习提问
1.解直角三角形:在直角三角形中,除一个直角外,还有2个角和3条边共5个元素,由已知元素求出未知元素的过程,叫做解直角三角形。
2.解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
3.在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′。
二.例题讲解
例2 如图25.3.2,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
分析:分析题目所给条件,找出未知量与已知量间的关系。计算方法不止一种,可选择适当的方法。
解: 在Rt△ABC中,
∠CAB=90゜-∠DAC=50゜,
=tan∠CAB,
∴BC=AB tan∠CAB=2000×tan50゜≈2384(米).
又∵ ,
∴AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米。
三.课堂练习
P95(练习):2
四.归纳小结:
1.请你小结测量物体的高度的几种方法;
2.如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离。
五.课后作业
P98(习题25.3):2
六.教学反思:
25.3 解直角三角形(3)
教学目标:
1.会运用解直角三角形有关知识解决有关仰角俯角的实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:
会运用解直角三角形有关知识解决有关仰角俯角的实际问题
教学难点:
会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.新知识点提
读一读
如图25.3.3,在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
二.例题讲解
例3 如图25.3.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
解 在Rt△BDE中,
BE=DE×tan a
=AC×tan a
=22.7×tan 22°
≈9.17,
所以 AB=BE+AE
=BE+CD
=9.17+1.20≈10.4(米).
答: 电线杆的高度约为10.4米.
[注意:]当题目中要求取近似值时,计算过程应比题目要求多取一位近似值。如该例题中要求精确到0.1米,则在计算过程中应先精确到0.01米。
三.课堂练习
P96(练习):1、2
四.归纳小结:
谈学习这节课的感受(怎样用数学知识解决实际生活中的问题)
五.课后作业
P98(习题25.3):3
六.教学反思:
25.3 解直角三角形(4)
教学目标:
1.会运用解直角三角形有关知识解决有关仰角俯角的实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:
会运用解直角三角形有关知识解决有关仰角俯角的实际问题
教学难点:
会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.新知识点提
读一读
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图25.3.5,坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比).记作i,即i=.
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,有
i==tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
二.例题讲解
例4 如图25.3.6,一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到
0.1米)
解 作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4.2(米),
CD=EF=12.51(米).
在Rt△ADE中,∵
∴
在Rt△BCF中,同理可得
∴ AB=AE+EF+BF
≈6.72+12.51+7.90≈27.13(米).
答: 路基下底的宽约为27.13米.
三.课堂练习
P98(练习)
四.归纳小结:
小结本课所学知识的感受
五.课后作业
P98(习题25.3):4
六.教学反思:
小结与复习(1)
教学目标
1.复习本章知识结构;
2.巩固勾股定理、三角函数和解直角三角形的相关知识;
教学重点:
勾股定理、锐角三角函数和解直角三角形的应用
教学难点:
锐角三角函数的概念
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.知识结构
二.概括
1. 了解勾股定理的历史,经历勾股定理的探索过程;
2. 理解并掌握直角三角形中边角之间的关系;
3. 能应用直角三角形的边角关系解决有关实际问题.
三.例题讲解
如图,以Rt△ABC的三边向外作三个半圆,试探索三个半圆的面积之间的关系.
(第2题)
计算: 2cos 30°+cot 60°-2tan 45°
求下列直角三角形中字母的值:
4.如图,在直角坐标平面中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角a的正切值是,求:
(1) y的值; (2) 角a的正弦值.
5.如图,一个古代棺木被探明位于A点地下24米处.由于A点地面下有煤气管道,考古人员不能垂直向下挖掘,他们被允许从距A点8米的B点挖掘.考古人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
四.课堂练习
P101(复习题)
A组:1、3、4(2)(3)、5(2)(3)、10
五.归纳小结:
1.锐角三角函数的概念;
2. 勾股定理、锐角三角函数和解直角三角形的应用
六.课后作业:
P101(复习题)A组:6、7、8
七.教学反思:
小结与复习(2)
教学目标:
1.进一步巩固勾股定理、三角函数和解直角三角形的相关知识;
2.熟练掌握运用解直角三角形的相关知识解决实际问题,增强应用数学的意识。
教学重点:
解直角三角形的应用
教学难点:
解直角三角形的应用
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.例题讲解
例 1: 一架25米的梯子靠在一座建筑物上,梯子的底部离建筑物7米.如果梯子的顶部滑下4米,梯子的底部滑开多远?
例2: 如图,两建筑物的水平距离BC为24米,从点A测得点D的俯角a=30°,测得点C的俯角b=60°,求AB和CD两座建筑物的高.(结果保留根号)
例 3: 在地面上一点A测得一电视塔的顶端的仰角为42°,再向电视塔方向前进120米,又测得电视塔的顶端的仰角为61°,求这个电视塔的高度.(精确到1米)
二.课堂练习
P102:9、11、12
三.归纳小结:
解直角三角形的应用
四.课后习题
P103C组14——16题
五.教学反思:
单元检测与评讲(4课时)
单元教学计划
本单元的主要内容是直角三角形的边角关系及其实际应用。教材先从测量入手,给学生创设学习情景,接着研究直角三角形的边角关系——锐角三角形函数,最后运用勾股定理及锐角三角函数等知识解决一些简单的实际问题。
教学目标:
1.经历由情境引出问题,探索掌握有关的数学知识内容,再运用于实践的过程,培养学数学、用数学的意识与能力。
2.通过实例认识直角三角形的边角关系,即锐角三角函数(sinA,cosA,tanA,cotA);知道30、45、60角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角。
3.运用三角函数解决与直角三角形有关的简单的实际问题。
4.能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题。
课时安排:本章教学时间约需14课时。具体分配如下:
25.1 测量 1课时
25.2 锐角三角函数 3课时
25.3 解直角三角形 4课时
复习 2课时
单元测验与评讲 4课时
第二十五章 解直角三角形
25.1 测 量
教学目标:
本节主要研究如何利用已学知识尤其是相似三角形的相关知识解决生活中某些测量问题。
教学重点:探究和解决生活中的某些测量问题。
教学难点:探究解决生活中的某些测量问题的方法。
教学方法;探究法
教具准备:皮尺、测角仪
教学过程:
一.问题引入
1.测量操场旗杆有多高?
如图25.1.1,站在操场上,请你的同学量出你在太阳下的影子长度、旗杆的影子长度,再根据你的身高,便可以计算出旗杆的高度.
图25.1.1
2.如果就你一个人,又遇上阴天,那怎么办呢?人们想到了一种可行的方法,还是利用相似三角形的知识.
二.试一试
如图25.1.2所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.现在请你按1∶500的比例将△ABC画在纸上,并记为△A′B′C′,用刻度直尺量出纸上B′C′的长度,便可以算出旗杆的实际高度.
你知道计算的方法吗?(请你量一量、算一算。)
实际上,我们利用图25.1.2(1)中已知的数据就可以直接计算旗杆的高度,而这一问题的解决将涉及到直角三角形中的边角关系.直角三角形中,三条边有什么关系?它的边与角又有什么关系?这一切都是本章要探究的内容.
三.课堂练习
1.在一次数学活动课上,老师让同学们到操场测量旗杆的高度,然后回来交流各自的测量方法。小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图所示),然后沿BC方向走到D处,这时目测旗杆顶部A到竹竿顶部E处恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高。
你认为这种测量方法是否可行?请说明理由。
2.请你与你的同学一起设计两种方案,测量你们学校楼房的高度。
四.归纳小结:
两种测量的方法:
方法一:构造可以测量的与原三角形相似的小三角形,利用对应线段成比例的性质计算出所求线段的长;
方法二:利用比例尺在纸上画一个与实物三角形相似的小三角形,通过直尺测量出所求线段在纸上的长度,再利用比例尺计算出实际长度。
五.课后作业
P87 习题25.1
六.教学反思:
25.2锐角三角函数
1 锐角三角函数
教学目标:
1.了解锐角三角函数的定义;
2.初步掌握三角函数的性质;
3.知道几种特殊角的三角函数值;
4.掌握定理:在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半。
教学重点:掌握几种特殊角的三角函数值和定理“在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半”。
教学难点:掌握三角函数的性质
教学方法:探究法
教具准备:直尺、电脑、实物投影
教学过程
一.复习引入
1.已知Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,问两个三角形的三组边是否成比例?
2.观察图25.2.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3中,
=__________=__________
=__________=__________
(可以使用几何画板演示)
结论:当Rt△ABC中,∠A的大小不变时,三条边的比例也不变(即为一个固定值)。
二.讲述新课
1.三角函数
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的.
因此这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A、cot A,即
sin A=, cos A=,
tan A=, cot A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
锐角三角函数的特征与性质:
(1)锐角三角函数的值都是正实数,并且0<sin A<1,0<cos A<1
(2)tan A cot A=1
(3)若∠A+∠B=90°,则sin A =cos B、cos A=sin B、tan A =cot B、cot A =tan B。
(4)补充:,(视情况定)
(5)补充:已知锐角∠A,则(视情况定)
3.例题讲解
求出图25.2.3所示的Rt△ABC中∠A的四个三角函数值.
解
sin A= cos A=
tan A= cot A=
4.探索:sin30゜=?
5.定理:在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半.
6.做一做:请填出空白处的值
三.课堂练习
P91(练习):1~4
四.归纳小结:
五.课后作业
P93(习题25.2):1~3
六.教学反思:
25.2锐角三角函数
用计算器求锐角三角函数值
教学目标:
1.会使用计算器求锐角三角函数的值;
2.会使用计算器根据锐角三角函数的值求对应的锐角。
教学重点:会使用计算器求锐角三角函数的值
教学难点:会使用计算器根据锐角三角函数的值求对应的锐角
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.讲述新课
1.如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角.
求已知锐角的三角函数值.
求sin63゜52′41″的值.(精确到0.0001)
解 先用如下方法将角度单位状态设定为“度”:
显示
再按下列顺序依次按键:
显示结果为0.897 859 012.
所以 sin63゜52′41″≈0.8979
例3 求cot70゜45′的值.(精确到0.0001)
解 在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序依次按键:
显示结果为0.349 215 633.
所以 cot70゜45′≈0.3492.
由锐角三角函数值求锐角
例4 已知tan x=0.7410,求锐角x.(精确到1′)
解 在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序
依次按键:
显示结果为36.538 445 77.
再按键:显示结果为36゜32′18.4.
所以,x≈36゜32′.
已知cot x=0.1950,求锐角x.(精确到1′)
分析 根据tan x=,可以求出tan x的值,然后根据例4的方法就可
以求出锐角x的值.
二.课堂练习
P93(练习):1~2
三.归纳小结:
四.作业:
P93(习题25.2):4~5
五.教学反思:
25.3 解直角三角形(1)
教学目标:
1.会运用三角函数解决与直角三角形有关的简单实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:
会运用三角函数解决与直角三角形有关的简单实际问题
教学难点:
会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:
探究法
教具准备:计算器、电脑、实物投影
教学过程
一.复习提问
复述勾股定理的内容:直角三角形两直角边的平方和等于斜边的平方.
锐角三角函数的定义:sin A=, cos A=,
tan A=, cot A= 。
锐角三角函数的特征与性质:
(1)锐角三角函数的值都是正实数,并且0<sin A<1,0<cos A<1
(2)tan A cot A=1
(3)若∠A+∠B=90°,则sin A =cos B、cos A=sin B、tan A =cot B、cot A =tan B。
(4)补充:,(视情况定)
(5)补充:已知锐角∠A,则(视情况定)
二.讲述新课
1.解直角三角形:在直角三角形中,除一个直角外,还有2个角和3条边共5个元素,由已知元素求出未知元素的过程,叫做解直角三角形。
2.例题讲解
例1: 在Rt△ABC中,∠C=90゜,已知,,解直角三角形。
分析:先根据条件画出三角形,可由勾股定理求出c,再由三角函数求锐角的度数。
[答案:,∠A=60°,∠B=30°]
例2(P93例1) 如图25.3.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
分析: 利用勾股定理求出折断倒下部分的长度,再求大树在折断前的高度。
[答案:36米]
三.归纳小结:
1.解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
2.在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.
四.课堂练习
P95练习第1题
五.课后作业:
P98习题25.3第1题
六.教学反思:
25.3 解直角三角形(2)
教学目标:
1.会运用三角函数解决与直角三角形有关的简单实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:会运用三角函数解决与直角三角形有关的简单实际问题
教学难点:会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.复习提问
1.解直角三角形:在直角三角形中,除一个直角外,还有2个角和3条边共5个元素,由已知元素求出未知元素的过程,叫做解直角三角形。
2.解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
3.在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′。
二.例题讲解
例2 如图25.3.2,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
分析:分析题目所给条件,找出未知量与已知量间的关系。计算方法不止一种,可选择适当的方法。
解: 在Rt△ABC中,
∠CAB=90゜-∠DAC=50゜,
=tan∠CAB,
∴BC=AB tan∠CAB=2000×tan50゜≈2384(米).
又∵ ,
∴AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米。
三.课堂练习
P95(练习):2
四.归纳小结:
1.请你小结测量物体的高度的几种方法;
2.如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离。
五.课后作业
P98(习题25.3):2
六.教学反思:
25.3 解直角三角形(3)
教学目标:
1.会运用解直角三角形有关知识解决有关仰角俯角的实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:
会运用解直角三角形有关知识解决有关仰角俯角的实际问题
教学难点:
会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.新知识点提
读一读
如图25.3.3,在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
二.例题讲解
例3 如图25.3.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
解 在Rt△BDE中,
BE=DE×tan a
=AC×tan a
=22.7×tan 22°
≈9.17,
所以 AB=BE+AE
=BE+CD
=9.17+1.20≈10.4(米).
答: 电线杆的高度约为10.4米.
[注意:]当题目中要求取近似值时,计算过程应比题目要求多取一位近似值。如该例题中要求精确到0.1米,则在计算过程中应先精确到0.01米。
三.课堂练习
P96(练习):1、2
四.归纳小结:
谈学习这节课的感受(怎样用数学知识解决实际生活中的问题)
五.课后作业
P98(习题25.3):3
六.教学反思:
25.3 解直角三角形(4)
教学目标:
1.会运用解直角三角形有关知识解决有关仰角俯角的实际问题;
2.会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题。
教学重点:
会运用解直角三角形有关知识解决有关仰角俯角的实际问题
教学难点:
会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.新知识点提
读一读
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图25.3.5,坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比).记作i,即i=.
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,有
i==tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
二.例题讲解
例4 如图25.3.6,一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到
0.1米)
解 作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4.2(米),
CD=EF=12.51(米).
在Rt△ADE中,∵
∴
在Rt△BCF中,同理可得
∴ AB=AE+EF+BF
≈6.72+12.51+7.90≈27.13(米).
答: 路基下底的宽约为27.13米.
三.课堂练习
P98(练习)
四.归纳小结:
小结本课所学知识的感受
五.课后作业
P98(习题25.3):4
六.教学反思:
小结与复习(1)
教学目标
1.复习本章知识结构;
2.巩固勾股定理、三角函数和解直角三角形的相关知识;
教学重点:
勾股定理、锐角三角函数和解直角三角形的应用
教学难点:
锐角三角函数的概念
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.知识结构
二.概括
1. 了解勾股定理的历史,经历勾股定理的探索过程;
2. 理解并掌握直角三角形中边角之间的关系;
3. 能应用直角三角形的边角关系解决有关实际问题.
三.例题讲解
如图,以Rt△ABC的三边向外作三个半圆,试探索三个半圆的面积之间的关系.
(第2题)
计算: 2cos 30°+cot 60°-2tan 45°
求下列直角三角形中字母的值:
4.如图,在直角坐标平面中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角a的正切值是,求:
(1) y的值; (2) 角a的正弦值.
5.如图,一个古代棺木被探明位于A点地下24米处.由于A点地面下有煤气管道,考古人员不能垂直向下挖掘,他们被允许从距A点8米的B点挖掘.考古人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
四.课堂练习
P101(复习题)
A组:1、3、4(2)(3)、5(2)(3)、10
五.归纳小结:
1.锐角三角函数的概念;
2. 勾股定理、锐角三角函数和解直角三角形的应用
六.课后作业:
P101(复习题)A组:6、7、8
七.教学反思:
小结与复习(2)
教学目标:
1.进一步巩固勾股定理、三角函数和解直角三角形的相关知识;
2.熟练掌握运用解直角三角形的相关知识解决实际问题,增强应用数学的意识。
教学重点:
解直角三角形的应用
教学难点:
解直角三角形的应用
教学方法:探究法
教具准备:计算器、电脑、实物投影
教学过程
一.例题讲解
例 1: 一架25米的梯子靠在一座建筑物上,梯子的底部离建筑物7米.如果梯子的顶部滑下4米,梯子的底部滑开多远?
例2: 如图,两建筑物的水平距离BC为24米,从点A测得点D的俯角a=30°,测得点C的俯角b=60°,求AB和CD两座建筑物的高.(结果保留根号)
例 3: 在地面上一点A测得一电视塔的顶端的仰角为42°,再向电视塔方向前进120米,又测得电视塔的顶端的仰角为61°,求这个电视塔的高度.(精确到1米)
二.课堂练习
P102:9、11、12
三.归纳小结:
解直角三角形的应用
四.课后习题
P103C组14——16题
五.教学反思:
单元检测与评讲(4课时)
