2020-2021学年高一数学人教A版 必修4 第一章1.6三角函数模型的简单应用 课件(共19张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版 必修4 第一章1.6三角函数模型的简单应用 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 595.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 11:00:27 | ||
图片预览




文档简介
(共19张PPT)
教学目标:掌握由已知图象和数据求函数解析式的方法;加强用三角函数模型刻画周期变换现象,解决实际问题的能力.
教学重点:用三角函数模型解决一些具有周
期变化规律的实际问题.
教学难点:将某些实际问题抽象为三角函数
模型;利用收集到的数据作出散点图,并进行函数拟合,从而得到函数模型.
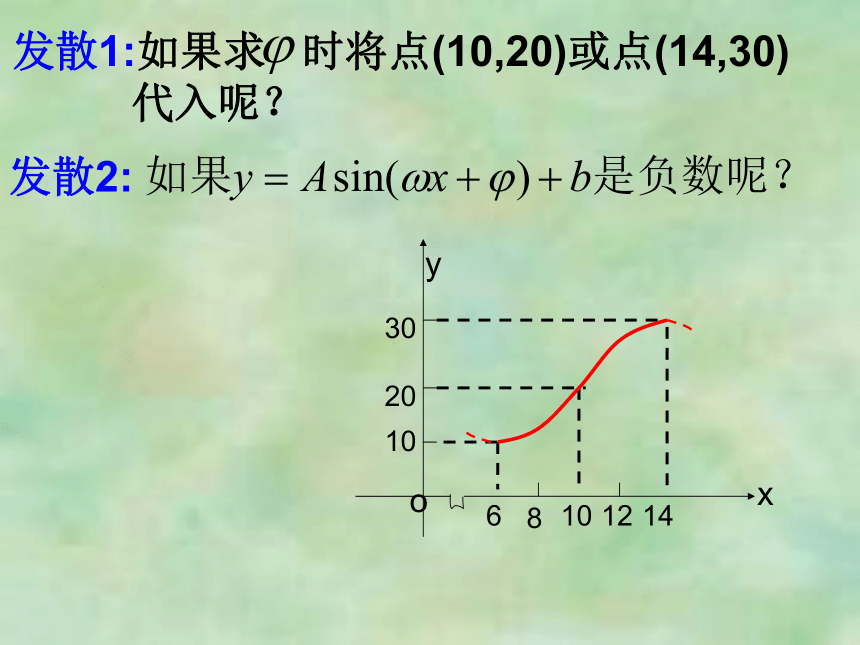
例1
如图所示,某地一天从6~14时的温度变
化曲线近似满足函数
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
x
o
8
6
y
10
14
12
10
30
20
小结:本题是研究温度随时间呈周期性变化的问题.在解决问题时要注意所给的曲线,求出函数解析式,要特别注意自变量的变化范围.
总结:求
的方法。
x
o
8
6
y
10
14
12
10
30
20
发散1:如果求
时将点(10,20)或点(14,30)
代入呢?
发散2:
巩固练习:
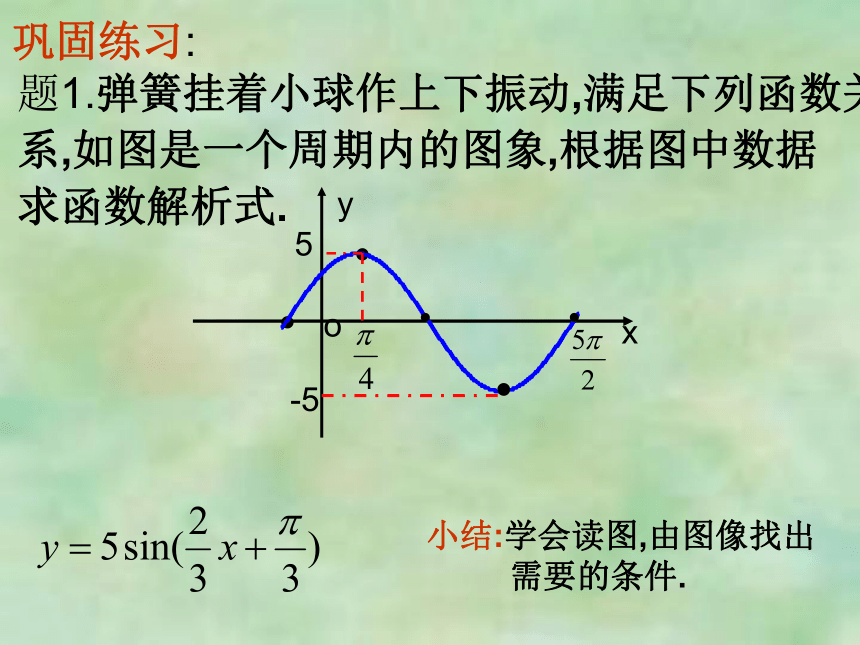
题1.弹簧挂着小球作上下振动,满足下列函数关
系,如图是一个周期内的图象,根据图中数据
求函数解析式.
小结:学会读图,由图像找出
需要的条件.
x
y
o
5
-5
的解析式
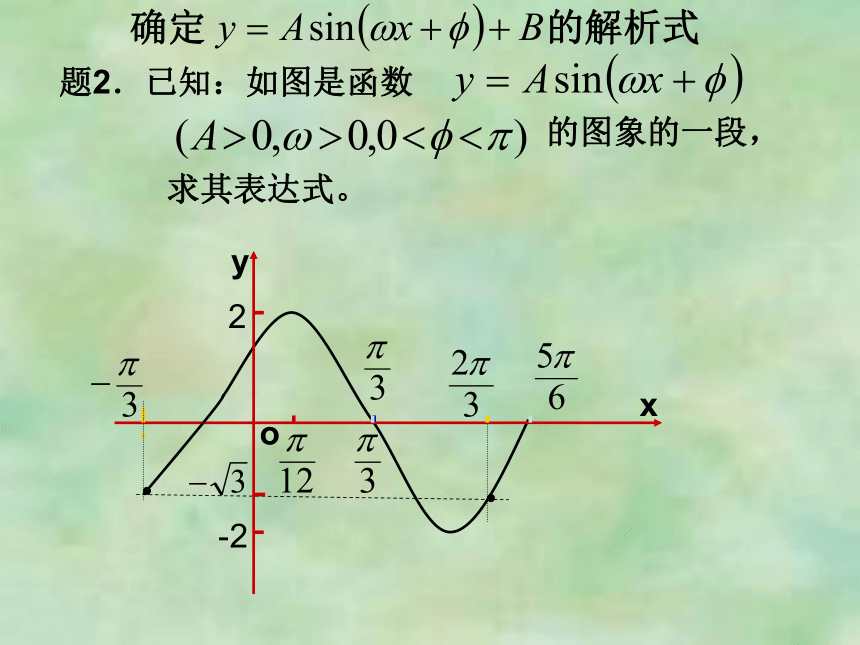
确定
题2.已知:如图是函数
o
的图象的一段,
求其表达式。
x
2
-2
y
2
-2
X
Y
o
2
-2
X
Y
O
归纳:利用
的特殊
位置求
归纳:利用
最值求
归纳:根据
图象上任意一点
确定
x
2
-2
y
o
例2
海水受日月的引力,在一定的时候发生涨
落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在
通常情况下,船在涨潮时驶进行道,靠近码头;
卸货后,在落潮时返回海洋.下面是某港口在某
季节每天的时间与水深关系表:
x(h)
0
3
6
9
12
15
18
21
24
y(m)
5.0
7.5
5.0
2.5
5.0
7.5
5.0
2.5
5.0
(1)请根据以上数据,选用一个函数近似描述
这个港口的水深与时间的函数关系,并求出
函数解析式.
分析:水深的变化具有周期性,根据图中的数据作出散点图,从散点判断,这个港口的水深与
时间的关系可以用形如
的函数来刻画,其中
是时间,
是水深.根据
所给数据可以具体确定
的值.
(2)一条货船的吃水深度(船底与水面的距离)
为4米,安全条例规定至少要有1.5米的安全
间隙(船底与海底的距离),那么该船何时能够安全进出港?
小结:解题时应注意探求表格中的规律,画出散点
图,选择合适的函数模型,依据题意分析问题,解决
问题;并注意考虑问题的实际意义.
(3)若该船必须在当天安全进港和出港,它在
港口停留的时间最多有多少小时?
巩固练习:
已知某海滨浴场海浪的高度
米是时间
(
单位:小时)的函数,记作:
下表是某日各时的浪高数据:
t(时)
0
3
6
9
12
15
18
21
24
y(米)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经过长期观察,此函数的曲线可近似地看成
是函数
的曲线.
(1)根据以上数据,你能否选用一个函数来近似
描述这个函数关系,并求出其解析式.
(2)依据规定,当海浪高度高于1米时才对冲浪
爱好者开放,请依据(1)的结论,判断一天内
的上午8:00时至晚上20:00时之间,有多少
时间可供冲浪爱好者运动?
(2)上午9:00至下午3:00
例3
如图,点P是半径为rcm的砂轮边缘上的
一个质点,它从初始位置P0
开始,按逆时针方
向以角速度
作圆周运动,求:
(1)P的纵坐标y关于时间
t的函数解析式;
o
P
P0
(3)如果
(4)
在(3)条件下,试求P点到达x轴的正半轴所
需的时间.
(2)点P的运动周期的频率;
分析:数形结合,利用三角函数的定义以及三角函数线,建立P点的纵坐标y与时间t之间的函数关系式,这是本题的关键.
解:(1)如图所示,
(2)由(1)可知,
小结:解题时应充分利用图形分析问题,且注意
物理知识和数学的综合运用.
(4)设小球经过时间t后到达x轴的正半轴,令
小结
1.确定函数解释式
参数的确定:
A,b:
利用最值;
w:利用周期;
:
小结
2.利用三角函数模型解应用题的步骤:
(1)阅读理解,审清题意;
(2)搜集整理数据,建立数学模型;
(3)利用所学的三角函数知识对得到的三角
函数模型进行解答,求的结果;
(4)将所得结论转译成实际问题的答案.
3.体会三角函数模型的特点,体验数学在解决实际
问题中的价值和作用,以及数学与日常生活和其
他学科的联系,逐步提高创新意识和实践能力.
本节课是对整章三角函数的一个应用,在讲解时要注意培养学生分析问题,解决问题的能力。
教学目标:掌握由已知图象和数据求函数解析式的方法;加强用三角函数模型刻画周期变换现象,解决实际问题的能力.
教学重点:用三角函数模型解决一些具有周
期变化规律的实际问题.
教学难点:将某些实际问题抽象为三角函数
模型;利用收集到的数据作出散点图,并进行函数拟合,从而得到函数模型.
例1
如图所示,某地一天从6~14时的温度变
化曲线近似满足函数
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
x
o
8
6
y
10
14
12
10
30
20
小结:本题是研究温度随时间呈周期性变化的问题.在解决问题时要注意所给的曲线,求出函数解析式,要特别注意自变量的变化范围.
总结:求
的方法。
x
o
8
6
y
10
14
12
10
30
20
发散1:如果求
时将点(10,20)或点(14,30)
代入呢?
发散2:
巩固练习:
题1.弹簧挂着小球作上下振动,满足下列函数关
系,如图是一个周期内的图象,根据图中数据
求函数解析式.
小结:学会读图,由图像找出
需要的条件.
x
y
o
5
-5
的解析式
确定
题2.已知:如图是函数
o
的图象的一段,
求其表达式。
x
2
-2
y
2
-2
X
Y
o
2
-2
X
Y
O
归纳:利用
的特殊
位置求
归纳:利用
最值求
归纳:根据
图象上任意一点
确定
x
2
-2
y
o
例2
海水受日月的引力,在一定的时候发生涨
落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在
通常情况下,船在涨潮时驶进行道,靠近码头;
卸货后,在落潮时返回海洋.下面是某港口在某
季节每天的时间与水深关系表:
x(h)
0
3
6
9
12
15
18
21
24
y(m)
5.0
7.5
5.0
2.5
5.0
7.5
5.0
2.5
5.0
(1)请根据以上数据,选用一个函数近似描述
这个港口的水深与时间的函数关系,并求出
函数解析式.
分析:水深的变化具有周期性,根据图中的数据作出散点图,从散点判断,这个港口的水深与
时间的关系可以用形如
的函数来刻画,其中
是时间,
是水深.根据
所给数据可以具体确定
的值.
(2)一条货船的吃水深度(船底与水面的距离)
为4米,安全条例规定至少要有1.5米的安全
间隙(船底与海底的距离),那么该船何时能够安全进出港?
小结:解题时应注意探求表格中的规律,画出散点
图,选择合适的函数模型,依据题意分析问题,解决
问题;并注意考虑问题的实际意义.
(3)若该船必须在当天安全进港和出港,它在
港口停留的时间最多有多少小时?
巩固练习:
已知某海滨浴场海浪的高度
米是时间
(
单位:小时)的函数,记作:
下表是某日各时的浪高数据:
t(时)
0
3
6
9
12
15
18
21
24
y(米)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经过长期观察,此函数的曲线可近似地看成
是函数
的曲线.
(1)根据以上数据,你能否选用一个函数来近似
描述这个函数关系,并求出其解析式.
(2)依据规定,当海浪高度高于1米时才对冲浪
爱好者开放,请依据(1)的结论,判断一天内
的上午8:00时至晚上20:00时之间,有多少
时间可供冲浪爱好者运动?
(2)上午9:00至下午3:00
例3
如图,点P是半径为rcm的砂轮边缘上的
一个质点,它从初始位置P0
开始,按逆时针方
向以角速度
作圆周运动,求:
(1)P的纵坐标y关于时间
t的函数解析式;
o
P
P0
(3)如果
(4)
在(3)条件下,试求P点到达x轴的正半轴所
需的时间.
(2)点P的运动周期的频率;
分析:数形结合,利用三角函数的定义以及三角函数线,建立P点的纵坐标y与时间t之间的函数关系式,这是本题的关键.
解:(1)如图所示,
(2)由(1)可知,
小结:解题时应充分利用图形分析问题,且注意
物理知识和数学的综合运用.
(4)设小球经过时间t后到达x轴的正半轴,令
小结
1.确定函数解释式
参数的确定:
A,b:
利用最值;
w:利用周期;
:
小结
2.利用三角函数模型解应用题的步骤:
(1)阅读理解,审清题意;
(2)搜集整理数据,建立数学模型;
(3)利用所学的三角函数知识对得到的三角
函数模型进行解答,求的结果;
(4)将所得结论转译成实际问题的答案.
3.体会三角函数模型的特点,体验数学在解决实际
问题中的价值和作用,以及数学与日常生活和其
他学科的联系,逐步提高创新意识和实践能力.
本节课是对整章三角函数的一个应用,在讲解时要注意培养学生分析问题,解决问题的能力。
