一年级上册数学教案-5.4 整理与提高(加倍与一半) 沪教版
文档属性
| 名称 | 一年级上册数学教案-5.4 整理与提高(加倍与一半) 沪教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 84.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览



文档简介
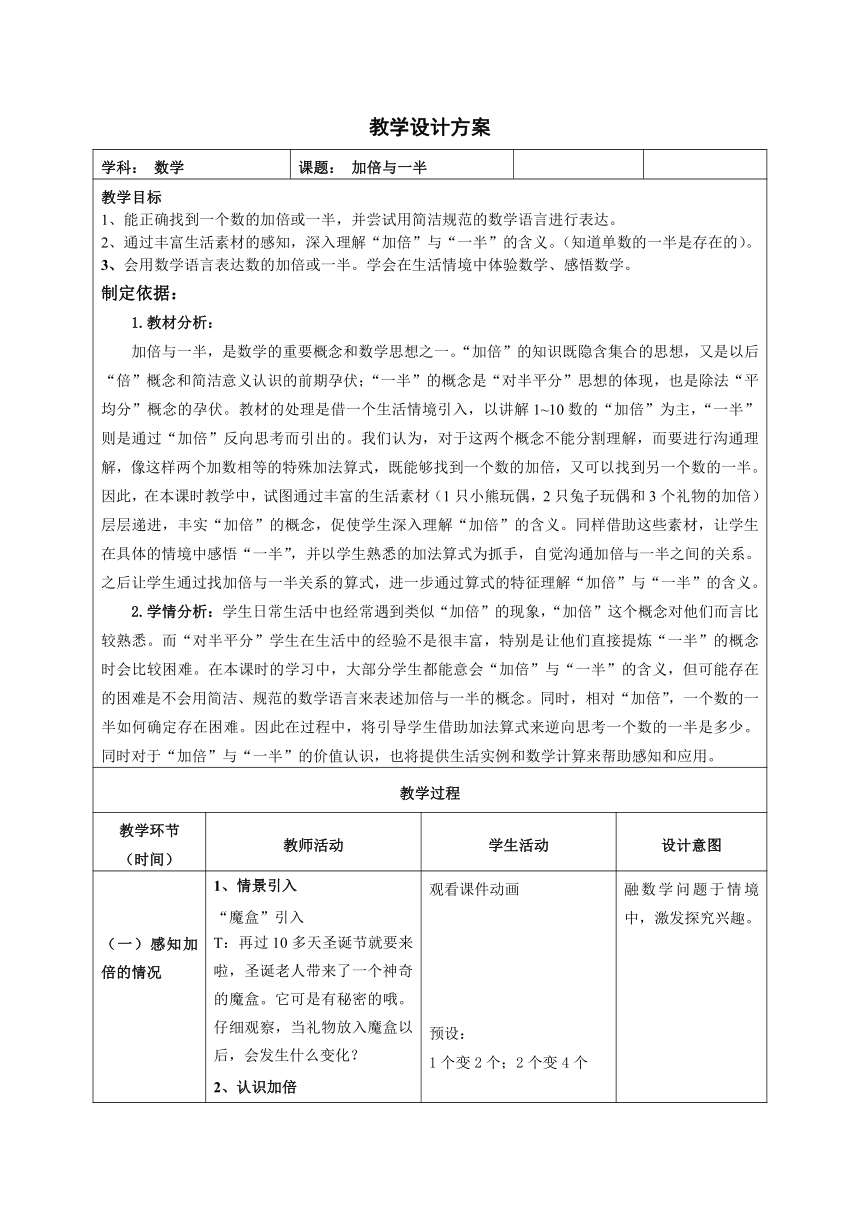
教学设计方案
学科: 数学 课题: 加倍与一半
教学目标 能正确找到一个数的加倍或一半,并尝试用简洁规范的数学语言进行表达。
通过丰富生活素材的感知,深入理解“加倍”与“一半”的含义。(知道单数的一半是存在的)。
会用数学语言表达数的加倍或一半。学会在生活情境中体验数学、感悟数学。
制定依据:
1.教材分析:
加倍与一半,是数学的重要概念和数学思想之一。“加倍”的知识既隐含集合的思想,又是以后“倍”概念和简洁意义认识的前期孕伏;“一半”的概念是“对半平分”思想的体现,也是除法“平均分”概念的孕伏。教材的处理是借一个生活情境引入,以讲解1~10数的“加倍”为主,“一半”则是通过“加倍”反向思考而引出的。我们认为,对于这两个概念不能分割理解,而要进行沟通理解,像这样两个加数相等的特殊加法算式,既能够找到一个数的加倍,又可以找到另一个数的一半。因此,在本课时教学中,试图通过丰富的生活素材(1只小熊玩偶,2只兔子玩偶和3个礼物的加倍)层层递进,丰实“加倍”的概念,促使学生深入理解“加倍”的含义。同样借助这些素材,让学生在具体的情境中感悟“一半”,并以学生熟悉的加法算式为抓手,自觉沟通加倍与一半之间的关系。之后让学生通过找加倍与一半关系的算式,进一步通过算式的特征理解“加倍”与“一半”的含义。
2.学情分析:学生日常生活中也经常遇到类似“加倍”的现象,“加倍”这个概念对他们而言比较熟悉。而“对半平分”学生在生活中的经验不是很丰富,特别是让他们直接提炼“一半”的概念时会比较困难。在本课时的学习中,大部分学生都能意会“加倍”与“一半”的含义,但可能存在的困难是不会用简洁、规范的数学语言来表述加倍与一半的概念。同时,相对“加倍”,一个数的一半如何确定存在困难。因此在过程中,将引导学生借助加法算式来逆向思考一个数的一半是多少。同时对于“加倍”与“一半”的价值认识,也将提供生活实例和数学计算来帮助感知和应用。
教学过程
教学环节 (时间) 教师活动 学生活动 设计意图
(一)感知加倍的情况
1、情景引入
“魔盒”引入
T:再过10多天圣诞节就要来啦,圣诞老人带来了一个神奇的魔盒。它可是有秘密的哦。仔细观察,当礼物放入魔盒以后,会发生什么变化?
2、认识加倍
T:那按照这样的规则,如果放入3个礼物,魔盒下会出现几个礼物呢?用一个小圆片表示一个礼物,谁来摆一摆出现几个礼物?
3、验证:是不是这样的呢?我们来验证一下。唉,确实像我们发现的这样,当我们放3个礼物,就出现了6个礼物。
4、反馈
T:你怎么知道是6个?
板书:同样多
关注小圆片
这三个小圆片表示什么意思?另外三个呢?
6、你发现了魔盒的秘密了吗?
原来魔盒的秘密就是添加了同样多的个数。原来有3个礼物,又添加了同样多的三个。(边说边圈小圆片)
7、提炼算式:3+3=6
T:能不能用一个算式来表示刚才的变化过程呢?
追问:这两个3的意思一样吗?
观看课件动画
预设:
1个变2个;2个变4个
学生上来摆
交流想法
预设:放进去了3个,又加了3个
预设:
放进去的3个,又加了3个。
2、原来3个礼物
经过魔盒又添加的3个礼物
放进去几个,又加了同样多的几个。
学生回答:3+3=6
不一样,第一个3表示原来的,第二个3表示添加的 融数学问题于情境中,激发探究兴趣。
从观察中发现规律。
引导学生用完整、规范的语言表述加倍的过程。
(二)聚焦算式特点与含义
1、尝试用算式表示前两个变化
T:你能不能回忆下前两个的变化?(小朋友说老师摆小圆片)
2、观察分析算式特点
T:观察这些加法算式,你发现他们有什么共同特点吗?
1、原来有1个,又添加了同样多的1个。齐说算式
2、原来有2个,又添加了同样多的2个。齐说算式
先独立思考,再同桌讨论
(1)横向:双数
(2)纵向:相同加数
培养分析、观察能力,感悟算式的含义。
(三)认识“加倍”与“一半”的关系
(四)辨析“加倍”与“一半”关系的算式
1、揭示概念(加倍的含义)
T:我们把原来的数量看做一份,那么添加同样多的一份,这种现象叫做“加倍”。
模仿:因为3+3=6,所以3的加倍是6。
练习2、3的加倍
2、一半的含义
T:因为3+3=6,所以3的加倍是6。听仔细哦,反过来也可以说6的一半是3。那一半是什么意思呢?
举例:1+5=6,可以说1是6的一半吗?5是6的一半吗?
小结:一半就是“把总数对半平分成同样多的两份,其中的一份是总数的“一半”。”
3、揭题:“加倍与一半”
小结:刚才我们通过这样的特殊的算式3+3=6,既找到了3的加倍是6,反过来还找到了6的一半是3。可以说:3+3=6,所以3的加倍是6,6的一半是3.
4、 4、巩固说法:1、2的加倍与一半 半
按照刚才的话同桌互说1和2的 加倍与一半。
T:老师这里有些算式,仔细观察:下面哪些算式能找到加倍与一半的关系?
T:为什么要选4+4=8而不选3+5=8呢?
小结:只有这样相同加数的算式才能帮助我们找到加倍与一半的关系。
齐说3的加倍
同桌互说
预设:分成一样多的就是一半
不可以,不是一样多的。
模仿老师用完整、规范的语言表述3的加倍与一半,同桌互说。
同桌互说。
反馈:分男生、女生齐说。
通过点头、摇头判断
预设:要加数相同的算式
感知加倍的含义。
初步感知“一半”的含义。
引导学生用完整、规范的语言表述3的加倍与一半
熟练地用数学语言表达数的加倍与一半。
判断加倍与一半的关系
巩固算式的特点和意义。
二、练习巩固
1、基础跟进练习
T:猫头鹰博士想考考我们的小朋友是不是学会加倍与一半的本领?你看他带来了几道题,仔细观察,这道题的要求是什么?
1、
反馈:你是怎么填的?你是怎么想的?
小结:看来这样一个特殊的加法算式,不仅能帮我们找到几的加倍,也可以反过来帮我们找到的结果的一半。
2、填上合适的数。
T:能不能用刚才的本领,你能看懂这样的表格吗?谁能举个例子来说说。
(投影展示)
T:(过程中)为什么第三列和第四列都是8而填的结果不一样呢?
3、情景练习
T:小猴子和小狗邀请大家去他们家做客,你能根据他们给的信息找到他们的家吗?小猴子说:我家的门牌号的一半是6,小狗说:我家的门牌号是2的加倍,再加倍。你知道他们的家分别是几号吗?跟你的同桌讨论一下,你是怎么想的?
小结:在找数加倍与一半的时,我们可以借助这样的表达式来帮助我们理清他们之间的关系并找到加倍或者一半。
独立完成
反馈交流
思考并填写练习卷
预设:
第一个8是16的一半,第二个8是4的加倍。
同桌讨论
集体反馈
预设:6+6=12
2 4 8
从具象到抽象,能正确求出一个数的加倍以及一个数的一半。
能用正向和逆向思路正确求出一个数的加倍以及一个数的一半。
借助模型解决问题
三、拓展(运用到生活和数学中) (一)生活中运用
T:看来在数学中,加倍与一半派上了很大的用场,那生活中有没有用到了加倍与一半的知识呢?我们来找找看。
1、购物情景 (买一送一&全场半价)
T:超市里我们经常看到“买一送一”、“全场半价”能不能用今天的知识来解释解释?
(二)数学中运用
1、利用加倍算式,进行推算 6+7=?
T:这是一道进位加法题,你能利用今天学习的知识来解决吗?
利用加倍算式,解决问题
T:这是我们做过的题目,通过今天对加倍与一半的学习,你发现了什么?
小结:看来加倍与一半不仅在生活中普遍存在,在数学应用中也帮助了我们很多。
拓展
我们学习了双数的一半,你知道单数有一半吗?这里有一个巧克力金币表示1,你觉得它有一半吗?(验证)
“买一送一”其实就是加倍。
“全场半价”其实就是价格变成原来的一半。
同桌讨论。
反馈:6+7= 既可以先想我们熟悉的6+6=12,然后再加1。就能得到13.也可以想7+7=14.然后再减1.
反馈:☆的加倍是18, △的加倍是12.
预设:一半巧克力
理解生活中的加倍与一半
用加倍算式解决数学问题。
用所学知识解决问题。
知道单数的一半是存在的
板书:
加倍与一半
加倍
1+1=2 1 2
一半
加倍
2+2=4 2 4
一半
加倍
3+3=6 3 6
学科: 数学 课题: 加倍与一半
教学目标 能正确找到一个数的加倍或一半,并尝试用简洁规范的数学语言进行表达。
通过丰富生活素材的感知,深入理解“加倍”与“一半”的含义。(知道单数的一半是存在的)。
会用数学语言表达数的加倍或一半。学会在生活情境中体验数学、感悟数学。
制定依据:
1.教材分析:
加倍与一半,是数学的重要概念和数学思想之一。“加倍”的知识既隐含集合的思想,又是以后“倍”概念和简洁意义认识的前期孕伏;“一半”的概念是“对半平分”思想的体现,也是除法“平均分”概念的孕伏。教材的处理是借一个生活情境引入,以讲解1~10数的“加倍”为主,“一半”则是通过“加倍”反向思考而引出的。我们认为,对于这两个概念不能分割理解,而要进行沟通理解,像这样两个加数相等的特殊加法算式,既能够找到一个数的加倍,又可以找到另一个数的一半。因此,在本课时教学中,试图通过丰富的生活素材(1只小熊玩偶,2只兔子玩偶和3个礼物的加倍)层层递进,丰实“加倍”的概念,促使学生深入理解“加倍”的含义。同样借助这些素材,让学生在具体的情境中感悟“一半”,并以学生熟悉的加法算式为抓手,自觉沟通加倍与一半之间的关系。之后让学生通过找加倍与一半关系的算式,进一步通过算式的特征理解“加倍”与“一半”的含义。
2.学情分析:学生日常生活中也经常遇到类似“加倍”的现象,“加倍”这个概念对他们而言比较熟悉。而“对半平分”学生在生活中的经验不是很丰富,特别是让他们直接提炼“一半”的概念时会比较困难。在本课时的学习中,大部分学生都能意会“加倍”与“一半”的含义,但可能存在的困难是不会用简洁、规范的数学语言来表述加倍与一半的概念。同时,相对“加倍”,一个数的一半如何确定存在困难。因此在过程中,将引导学生借助加法算式来逆向思考一个数的一半是多少。同时对于“加倍”与“一半”的价值认识,也将提供生活实例和数学计算来帮助感知和应用。
教学过程
教学环节 (时间) 教师活动 学生活动 设计意图
(一)感知加倍的情况
1、情景引入
“魔盒”引入
T:再过10多天圣诞节就要来啦,圣诞老人带来了一个神奇的魔盒。它可是有秘密的哦。仔细观察,当礼物放入魔盒以后,会发生什么变化?
2、认识加倍
T:那按照这样的规则,如果放入3个礼物,魔盒下会出现几个礼物呢?用一个小圆片表示一个礼物,谁来摆一摆出现几个礼物?
3、验证:是不是这样的呢?我们来验证一下。唉,确实像我们发现的这样,当我们放3个礼物,就出现了6个礼物。
4、反馈
T:你怎么知道是6个?
板书:同样多
关注小圆片
这三个小圆片表示什么意思?另外三个呢?
6、你发现了魔盒的秘密了吗?
原来魔盒的秘密就是添加了同样多的个数。原来有3个礼物,又添加了同样多的三个。(边说边圈小圆片)
7、提炼算式:3+3=6
T:能不能用一个算式来表示刚才的变化过程呢?
追问:这两个3的意思一样吗?
观看课件动画
预设:
1个变2个;2个变4个
学生上来摆
交流想法
预设:放进去了3个,又加了3个
预设:
放进去的3个,又加了3个。
2、原来3个礼物
经过魔盒又添加的3个礼物
放进去几个,又加了同样多的几个。
学生回答:3+3=6
不一样,第一个3表示原来的,第二个3表示添加的 融数学问题于情境中,激发探究兴趣。
从观察中发现规律。
引导学生用完整、规范的语言表述加倍的过程。
(二)聚焦算式特点与含义
1、尝试用算式表示前两个变化
T:你能不能回忆下前两个的变化?(小朋友说老师摆小圆片)
2、观察分析算式特点
T:观察这些加法算式,你发现他们有什么共同特点吗?
1、原来有1个,又添加了同样多的1个。齐说算式
2、原来有2个,又添加了同样多的2个。齐说算式
先独立思考,再同桌讨论
(1)横向:双数
(2)纵向:相同加数
培养分析、观察能力,感悟算式的含义。
(三)认识“加倍”与“一半”的关系
(四)辨析“加倍”与“一半”关系的算式
1、揭示概念(加倍的含义)
T:我们把原来的数量看做一份,那么添加同样多的一份,这种现象叫做“加倍”。
模仿:因为3+3=6,所以3的加倍是6。
练习2、3的加倍
2、一半的含义
T:因为3+3=6,所以3的加倍是6。听仔细哦,反过来也可以说6的一半是3。那一半是什么意思呢?
举例:1+5=6,可以说1是6的一半吗?5是6的一半吗?
小结:一半就是“把总数对半平分成同样多的两份,其中的一份是总数的“一半”。”
3、揭题:“加倍与一半”
小结:刚才我们通过这样的特殊的算式3+3=6,既找到了3的加倍是6,反过来还找到了6的一半是3。可以说:3+3=6,所以3的加倍是6,6的一半是3.
4、 4、巩固说法:1、2的加倍与一半 半
按照刚才的话同桌互说1和2的 加倍与一半。
T:老师这里有些算式,仔细观察:下面哪些算式能找到加倍与一半的关系?
T:为什么要选4+4=8而不选3+5=8呢?
小结:只有这样相同加数的算式才能帮助我们找到加倍与一半的关系。
齐说3的加倍
同桌互说
预设:分成一样多的就是一半
不可以,不是一样多的。
模仿老师用完整、规范的语言表述3的加倍与一半,同桌互说。
同桌互说。
反馈:分男生、女生齐说。
通过点头、摇头判断
预设:要加数相同的算式
感知加倍的含义。
初步感知“一半”的含义。
引导学生用完整、规范的语言表述3的加倍与一半
熟练地用数学语言表达数的加倍与一半。
判断加倍与一半的关系
巩固算式的特点和意义。
二、练习巩固
1、基础跟进练习
T:猫头鹰博士想考考我们的小朋友是不是学会加倍与一半的本领?你看他带来了几道题,仔细观察,这道题的要求是什么?
1、
反馈:你是怎么填的?你是怎么想的?
小结:看来这样一个特殊的加法算式,不仅能帮我们找到几的加倍,也可以反过来帮我们找到的结果的一半。
2、填上合适的数。
T:能不能用刚才的本领,你能看懂这样的表格吗?谁能举个例子来说说。
(投影展示)
T:(过程中)为什么第三列和第四列都是8而填的结果不一样呢?
3、情景练习
T:小猴子和小狗邀请大家去他们家做客,你能根据他们给的信息找到他们的家吗?小猴子说:我家的门牌号的一半是6,小狗说:我家的门牌号是2的加倍,再加倍。你知道他们的家分别是几号吗?跟你的同桌讨论一下,你是怎么想的?
小结:在找数加倍与一半的时,我们可以借助这样的表达式来帮助我们理清他们之间的关系并找到加倍或者一半。
独立完成
反馈交流
思考并填写练习卷
预设:
第一个8是16的一半,第二个8是4的加倍。
同桌讨论
集体反馈
预设:6+6=12
2 4 8
从具象到抽象,能正确求出一个数的加倍以及一个数的一半。
能用正向和逆向思路正确求出一个数的加倍以及一个数的一半。
借助模型解决问题
三、拓展(运用到生活和数学中) (一)生活中运用
T:看来在数学中,加倍与一半派上了很大的用场,那生活中有没有用到了加倍与一半的知识呢?我们来找找看。
1、购物情景 (买一送一&全场半价)
T:超市里我们经常看到“买一送一”、“全场半价”能不能用今天的知识来解释解释?
(二)数学中运用
1、利用加倍算式,进行推算 6+7=?
T:这是一道进位加法题,你能利用今天学习的知识来解决吗?
利用加倍算式,解决问题
T:这是我们做过的题目,通过今天对加倍与一半的学习,你发现了什么?
小结:看来加倍与一半不仅在生活中普遍存在,在数学应用中也帮助了我们很多。
拓展
我们学习了双数的一半,你知道单数有一半吗?这里有一个巧克力金币表示1,你觉得它有一半吗?(验证)
“买一送一”其实就是加倍。
“全场半价”其实就是价格变成原来的一半。
同桌讨论。
反馈:6+7= 既可以先想我们熟悉的6+6=12,然后再加1。就能得到13.也可以想7+7=14.然后再减1.
反馈:☆的加倍是18, △的加倍是12.
预设:一半巧克力
理解生活中的加倍与一半
用加倍算式解决数学问题。
用所学知识解决问题。
知道单数的一半是存在的
板书:
加倍与一半
加倍
1+1=2 1 2
一半
加倍
2+2=4 2 4
一半
加倍
3+3=6 3 6
