5.4抛体运动的规律 课件 32张PPT
文档属性
| 名称 | 5.4抛体运动的规律 课件 32张PPT | 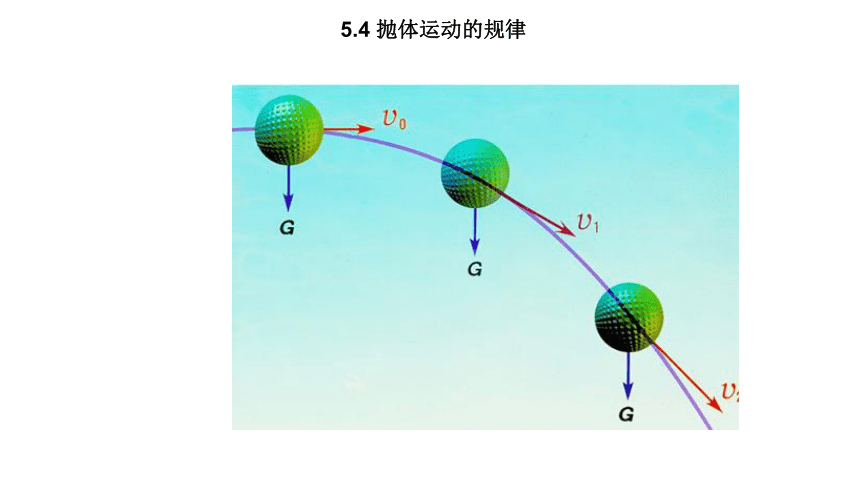 | |
| 格式 | ppt | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-08 19:38:06 | ||
图片预览








文档简介
5.4 抛体运动的规律
上节课我们通过实验探究了平抛运动的特点,本节我 们将从理论分析的角度,对抛体运动的规律作进一步分析。
一、平抛运动的速度
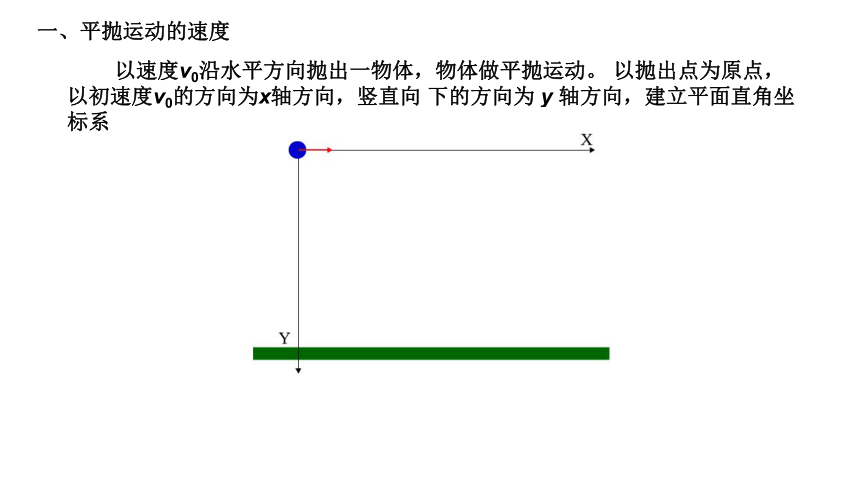
以速度v0沿水平方向抛出一物体,物体做平抛运动。 以抛出点为原点,以初速度v0的方向为x轴方向,竖直向 下的方向为 y 轴方向,建立平面直角坐标系
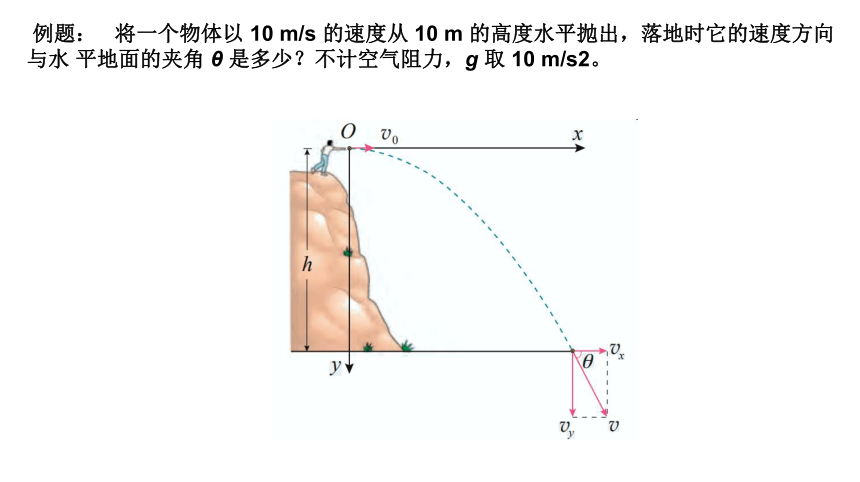
例题: 将一个物体以 10 m/s 的速度从 10 m 的高度水平抛出,落地时它的速度方向与水 平地面的夹角 θ 是多少?不计空气阻力,g 取 10 m/s2。
二、平抛运动的位移与轨迹
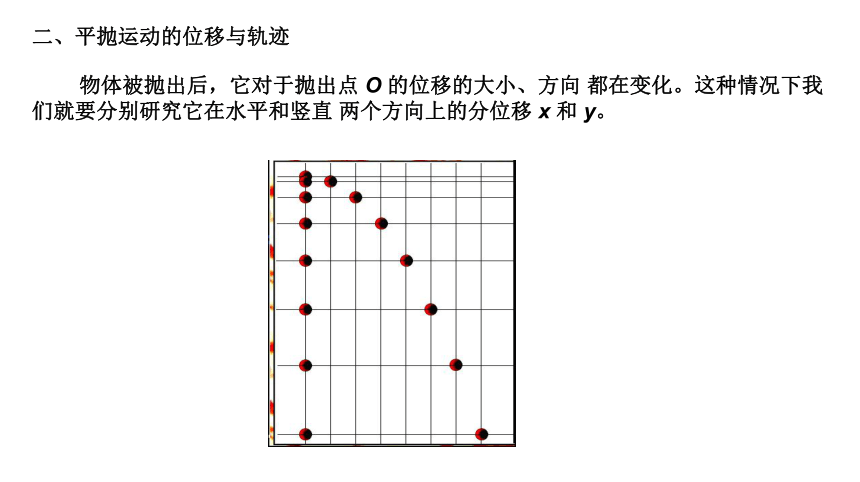
物体被抛出后,它对于抛出点 O 的位移的大小、方向 都在变化。这种情况下我们就要分别研究它在水平和竖直 两个方向上的分位移 x 和 y。
1、平抛运动的位移与轨迹
例题2:如图 5.4-3,某同学利用无人机玩“投弹”游戏。无人机以 v0=2m/s 的速度水平向右匀速飞行,在某时 刻释放了一个小球。此时无人机到水平地面的距离h=20 m,空气阻力忽略不计,g 取10 m/s2。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
三、一般的抛体运动
四、平抛运动的几个结论
4、平抛运动中的临界模型
(1)通过关键词来判断临界点、极值点
①有些题目中有“刚好”“恰好”“正好”等字眼,明显表明题述的过程中存在着临界点。
②若题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述的过程中存在着“起止点”,而这些“起止点”往往就是临界点。
③若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程中存在着极值,这些极值点也往往是临界点。
(2)分析处理方法
①确定临界状态及临界轨迹,并由此列出符合临界条件的物理方程。
②注意恰当运用数学知识分析求解临界与极值问题。
课堂练习:
2、在平坦的垒球运动场上,击球手挥动球棒将垒球水平击出,垒球飞行一段时间后落地.若不计空气阻力,则( )
A.垒球落地时瞬时速度的大小仅由初速度决定
B.垒球落地时瞬时速度的方向仅由击球点离地面的高度决定
C.垒球在空中运动的水平位移仅由初速度决定
D.垒球在空中运动的时间仅由击球点离地面的高度决定
6、斜面上有a、b、c、d四个点,如图所示,ab=bc=cd,从a点正上方的O点以速度v水平抛出一个小球,它落在斜面上b点。若小球从O点以速度2v水平抛出,不计空气阻力,则它落在斜面上的( )
A.c与d之间某一点 B.c点
C.b与c之间某一点 D.d点
解析:选C过b作一条与水平面平行的虚线,如图所示,若没有斜面,当小球从O点以速度2v水平抛出时,小球落在水平面上时水平位移变为原来的2倍,则小球将落在所画水平线上c点的正下方,但是现在有斜面的限制,小球将落在斜面上的b、c之间,故C正确。
解析:选CD A、B两球都做斜上抛运动,只受重力作用,加速度即为重力加速度,A项错误;在竖直方向上做竖直上抛运动,由于能上升的竖直高度相同,竖直分速度相等,所以两小球在空中飞行的时间相等,B项错误;由于B球的水平射程比较大,故B球的水平速度及落地时的速度均比A球的大,C、D正确.
上节课我们通过实验探究了平抛运动的特点,本节我 们将从理论分析的角度,对抛体运动的规律作进一步分析。
一、平抛运动的速度
以速度v0沿水平方向抛出一物体,物体做平抛运动。 以抛出点为原点,以初速度v0的方向为x轴方向,竖直向 下的方向为 y 轴方向,建立平面直角坐标系
例题: 将一个物体以 10 m/s 的速度从 10 m 的高度水平抛出,落地时它的速度方向与水 平地面的夹角 θ 是多少?不计空气阻力,g 取 10 m/s2。
二、平抛运动的位移与轨迹
物体被抛出后,它对于抛出点 O 的位移的大小、方向 都在变化。这种情况下我们就要分别研究它在水平和竖直 两个方向上的分位移 x 和 y。
1、平抛运动的位移与轨迹
例题2:如图 5.4-3,某同学利用无人机玩“投弹”游戏。无人机以 v0=2m/s 的速度水平向右匀速飞行,在某时 刻释放了一个小球。此时无人机到水平地面的距离h=20 m,空气阻力忽略不计,g 取10 m/s2。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
三、一般的抛体运动
四、平抛运动的几个结论
4、平抛运动中的临界模型
(1)通过关键词来判断临界点、极值点
①有些题目中有“刚好”“恰好”“正好”等字眼,明显表明题述的过程中存在着临界点。
②若题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述的过程中存在着“起止点”,而这些“起止点”往往就是临界点。
③若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程中存在着极值,这些极值点也往往是临界点。
(2)分析处理方法
①确定临界状态及临界轨迹,并由此列出符合临界条件的物理方程。
②注意恰当运用数学知识分析求解临界与极值问题。
课堂练习:
2、在平坦的垒球运动场上,击球手挥动球棒将垒球水平击出,垒球飞行一段时间后落地.若不计空气阻力,则( )
A.垒球落地时瞬时速度的大小仅由初速度决定
B.垒球落地时瞬时速度的方向仅由击球点离地面的高度决定
C.垒球在空中运动的水平位移仅由初速度决定
D.垒球在空中运动的时间仅由击球点离地面的高度决定
6、斜面上有a、b、c、d四个点,如图所示,ab=bc=cd,从a点正上方的O点以速度v水平抛出一个小球,它落在斜面上b点。若小球从O点以速度2v水平抛出,不计空气阻力,则它落在斜面上的( )
A.c与d之间某一点 B.c点
C.b与c之间某一点 D.d点
解析:选C过b作一条与水平面平行的虚线,如图所示,若没有斜面,当小球从O点以速度2v水平抛出时,小球落在水平面上时水平位移变为原来的2倍,则小球将落在所画水平线上c点的正下方,但是现在有斜面的限制,小球将落在斜面上的b、c之间,故C正确。
解析:选CD A、B两球都做斜上抛运动,只受重力作用,加速度即为重力加速度,A项错误;在竖直方向上做竖直上抛运动,由于能上升的竖直高度相同,竖直分速度相等,所以两小球在空中飞行的时间相等,B项错误;由于B球的水平射程比较大,故B球的水平速度及落地时的速度均比A球的大,C、D正确.
