2020-2021学年九年级下册数学青岛新版《第7章 空间图形的初步认识》单元测试题(word版含解析)
文档属性
| 名称 | 2020-2021学年九年级下册数学青岛新版《第7章 空间图形的初步认识》单元测试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 20:57:57 | ||
图片预览

文档简介
2020-2021学年九年级下册数学青岛新版《第7章
空间图形的初步认识》单元测试题
一.选择题
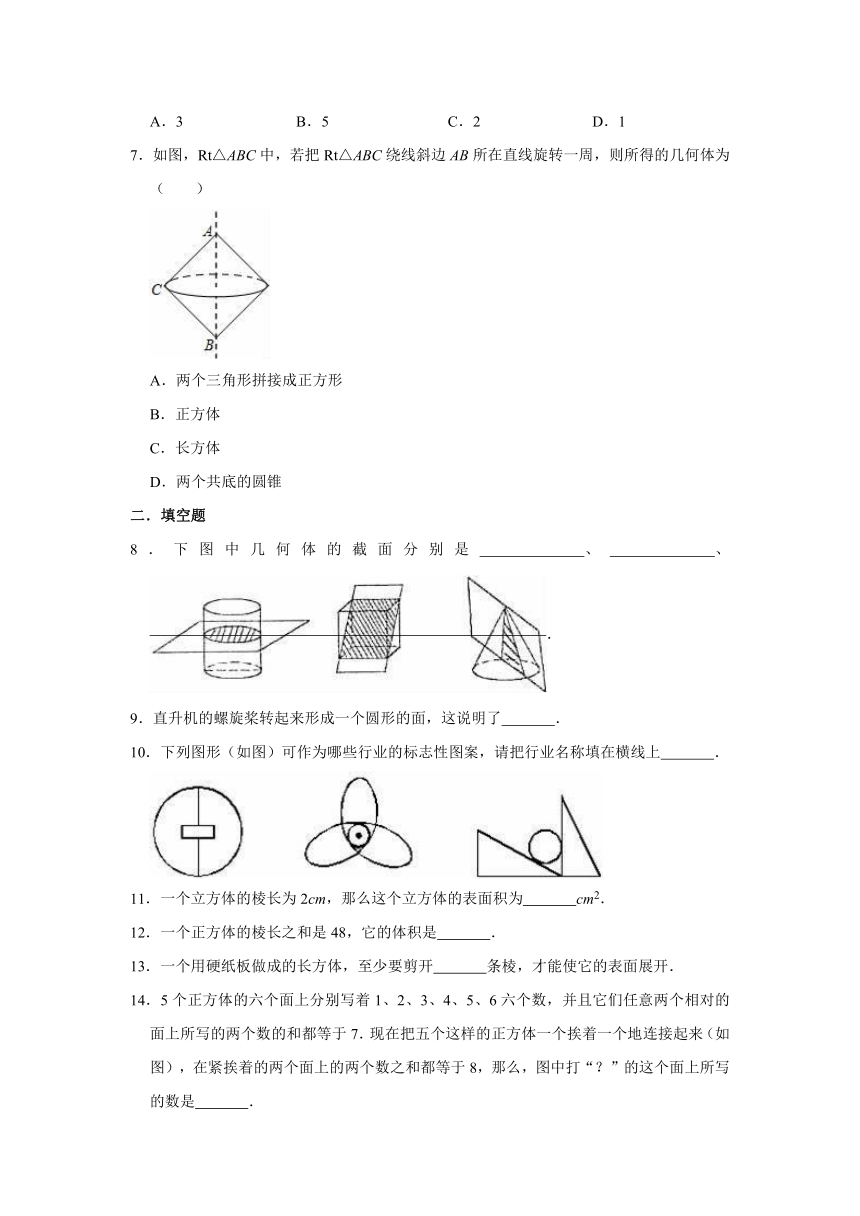
1.在长方形、长方体、三角形、球、直线、圆中,有( )个平面图形.
A.3
B.4
C.5
D.6
2.下列图形折叠起来不能做成一个开口的盒子的是( )
A.
B.
C.
D.
3.用一个平面去截一个长方体.截面的边数可能会出现的情况有( )
A.3种
B.4种
C.5种
D.6种
4.如图,在正方体中,AA1与AB,CC1,A1D1的关系分别是( )
A.垂直、平行、垂直
B.垂直、垂直、平行
C.垂直、平行、平行
D.以上都不对
5.一个正方体盒子的表面展开图如右所示,则这个纸盒的立体图形只能是( )
A.
B.
C.
D.
6.如图,每个长方体的六个面上分别写着1~6这六个数,并且任意两个相对的面上所写的两个数之和所写的两个数之和都等于7,靠在一起的长方体中,相连接两个面的数字之和等于8,图中打“?”的面上所写的数字是( )
A.3
B.5
C.2
D.1
7.如图,Rt△ABC中,若把Rt△ABC绕线斜边AB所在直线旋转一周,则所得的几何体为( )
A.两个三角形拼接成正方形
B.正方体
C.长方体
D.两个共底的圆锥
二.填空题
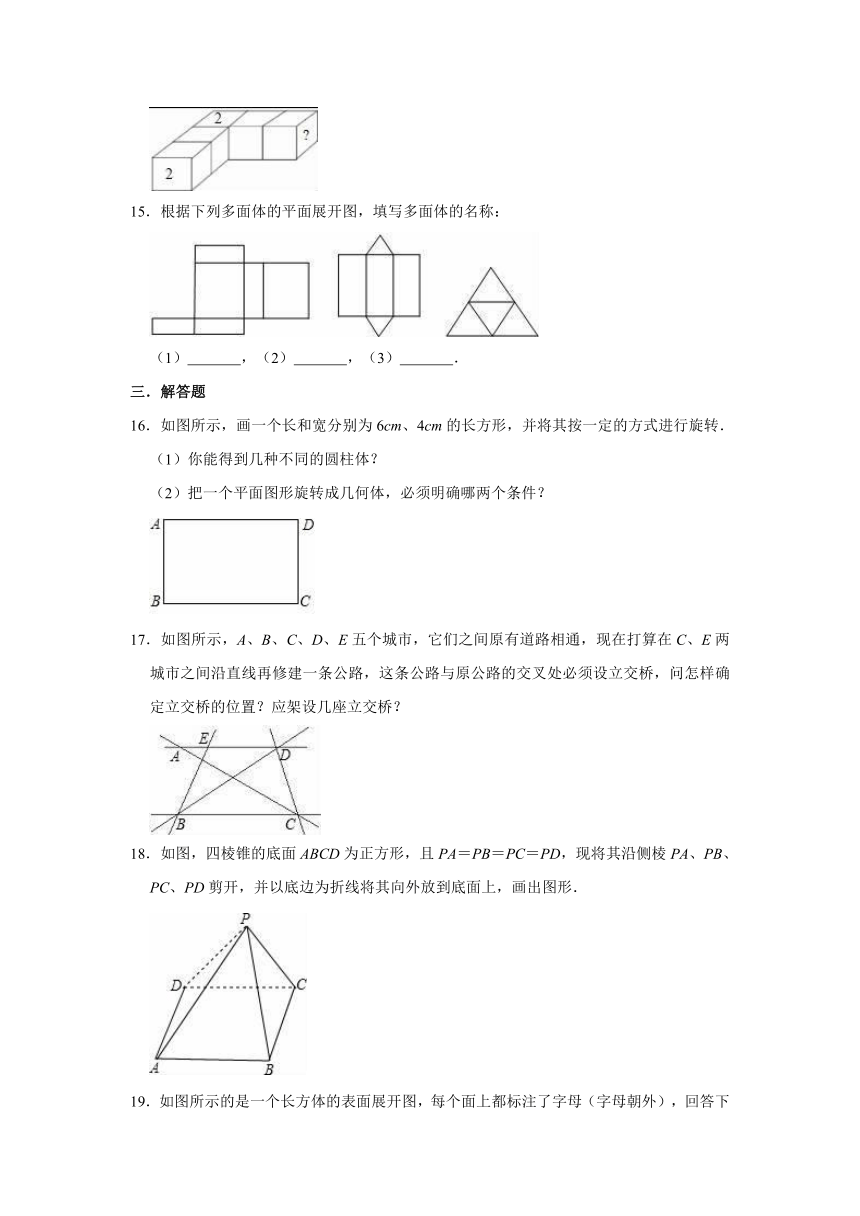
8.下图中几何体的截面分别是
、
、
.
9.直升机的螺旋桨转起来形成一个圆形的面,这说明了
.
10.下列图形(如图)可作为哪些行业的标志性图案,请把行业名称填在横线上
.
11.一个立方体的棱长为2cm,那么这个立方体的表面积为
cm2.
12.一个正方体的棱长之和是48,它的体积是
.
13.一个用硬纸板做成的长方体,至少要剪开
条棱,才能使它的表面展开.
14.5个正方体的六个面上分别写着1、2、3、4、5、6六个数,并且它们任意两个相对的面上所写的两个数的和都等于7.现在把五个这样的正方体一个挨着一个地连接起来(如图),在紧挨着的两个面上的两个数之和都等于8,那么,图中打“?”的这个面上所写的数是
.
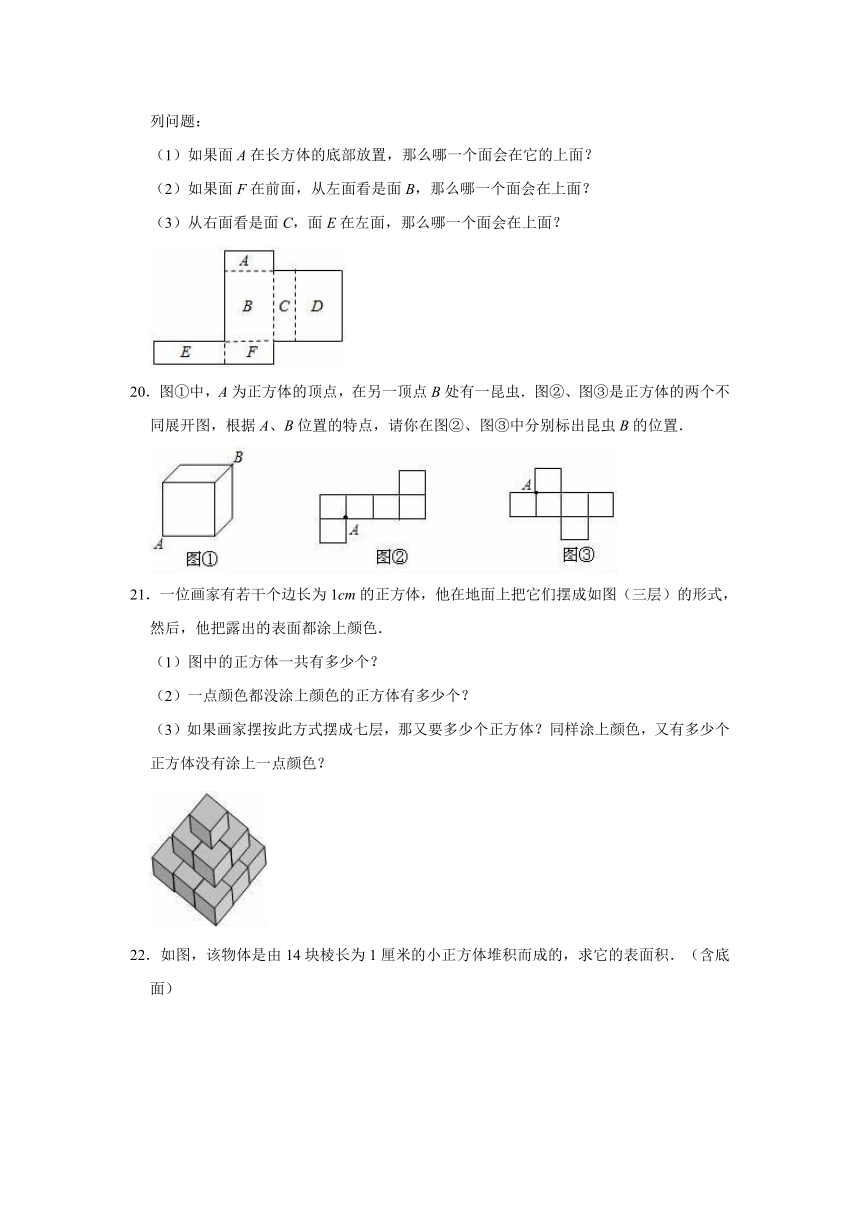
15.根据下列多面体的平面展开图,填写多面体的名称:
(1)
,(2)
,(3)
.
三.解答题
16.如图所示,画一个长和宽分别为6cm、4cm的长方形,并将其按一定的方式进行旋转.
(1)你能得到几种不同的圆柱体?
(2)把一个平面图形旋转成几何体,必须明确哪两个条件?
17.如图所示,A、B、C、D、E五个城市,它们之间原有道路相通,现在打算在C、E两城市之间沿直线再修建一条公路,这条公路与原公路的交叉处必须设立交桥,问怎样确定立交桥的位置?应架设几座立交桥?
18.如图,四棱锥的底面ABCD为正方形,且PA=PB=PC=PD,现将其沿侧棱PA、PB、PC、PD剪开,并以底边为折线将其向外放到底面上,画出图形.
19.如图所示的是一个长方体的表面展开图,每个面上都标注了字母(字母朝外),回答下列问题:
(1)如果面A在长方体的底部放置,那么哪一个面会在它的上面?
(2)如果面F在前面,从左面看是面B,那么哪一个面会在上面?
(3)从右面看是面C,面E在左面,那么哪一个面会在上面?
20.图①中,A为正方体的顶点,在另一顶点B处有一昆虫.图②、图③是正方体的两个不同展开图,根据A、B位置的特点,请你在图②、图③中分别标出昆虫B的位置.
21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
22.如图,该物体是由14块棱长为1厘米的小正方体堆积而成的,求它的表面积.(含底面)
参考答案与试题解析
一.选择题
1.解:平面图形有长方形,三角形,直线,圆共4个,故选B.
2.解:由正方体及其表面展开图的特点可知,
A、B、D能折叠起来做成一只开口的盒子,不符合题意;
B折叠后有两面重合,不能做成一个开口的盒子,符合题意.
故选:B.
3.解:用一个平面去截一个长方体,截面可能为三角形、四边形、五边形、六边形共有四种情况,
故选:B.
4.解:根据以上分析知:AA1与AB,CC1,A1D1的关系分别是垂直、平行、垂直.故选A.
5.解:A、字母A与竖线应是平行的关系,故A错误;
B、展开后与原图形符合,故正确;
C、字母A与竖线应是平行的关系,故C错误;
D、原图形折叠不成D的形式,错误.
故选:B.
6.解:由题意可知:每个长方体的六个面上分别写着1~6这六个数,且任意两个相对的面上所写的两个数之和为7,可知第一个长方体所对应的1的对面为6,
又知靠在一起的长方体中,相连接两个面的数字之和等于8,可知下一个长方体的前面为2,以此类推,可得结果为3.
故选:A.
7.解:根据题意可知是两个共底的圆锥.
故选:D.
二.填空题
8.解:当截面平行于圆柱底面截取圆柱时得到截面图形是圆,截面截取经过四个顶点的截面时可以截得长方形,当截面垂直圆锥的底面时,截面图形是三角形.
9.解:直升机的螺旋桨可以近似看做线段,
由线动成面可得,转起来形成一个圆形的面,
故答案为:线动成面.
10.解:第一个很像工商银行的标志,第二个含有一个圆可作为科技的标志,第三个有三角板可作为教育的标志.
故答案为:银行、与科技有关的项目、与教育有关的项目.
11.解:这个立方体的表面积为:
6×22=6×4=24(cm2).
故答案为24.
12.解:∵正方体的棱有12条,棱长之和是48,
∴每一条棱长为48÷12=4,
∴它的体积是:4×4×4=64,
故答案为:64.
13.解:一个用硬纸板做成的长方体,至少要剪开7条棱,才能使它的表面展开.
故答案为:7.
14.解:由题意可知:正方体的六个面上分别写着1、2、3、4、5、6六个数,并且它们任意两个相对的面上所写的两个数的和都等于7,故第一个正方体的后面为5,在紧挨着的两个面上的两个数之和都等于8,则与它相接的第二个正方体的前面为3,对面为4,依此类推,即可求得结果为4.
故答案为4.
15.解:由平面展开图的特征可知,从左边第一个是长方体,第二个是三棱柱,第三个是三棱锥.
三.解答题
16.解:(1)由于长和宽分别为6cm、4cm的长方形,旋转可得到四种不同的圆柱体;
①一长方形的一条长AD(或BC)所在直线为旋转轴,旋转360°,可得到底面半径为4cm,高为6cm的圆柱体;
②一长方形的一条宽AB(或CD)所在直线为旋转轴,旋转一周,可得到底面半径为6cm,高为4cm的圆柱体;
③以长方形的长AD、BC的中点G、H所在直线为旋转轴,旋转180°,可得到底面半径为3cm,高为4cm的圆柱体;
④以长方形的长AB、DC的中点E、F所在直线为旋转轴,旋转180°,可得到底面半径为2cm,高为6cm的圆柱体;
(2)把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
17.解:连接CE,与BD的交点处架立交桥;1座.
18.解:
19.解:(1)根据“相间、Z端是对面”可知,
“A”与“F”相对,
“B”与“D”相对,
“C”与“E“相对,
所以面A在长方体的底部,那么F个面会在它的上面;
(2)若面F在前面,左面是面B,则“A”在后面,“D”在右面,此时“C”在上面,“E”在下面,或“E”在上面,“C”在下面,
答:如果面F在前面,从左面看是面B,那么“C”面或“E”面会在上面;
(3)从右面看是面C,面E在左面,则“B”面或“D”面在上面.
20.解:
21.解:(1)图中的正方体一共有1+4+9=14个;
(2)一点颜色都没涂上颜色的正方体有1个;
(3)七层的正方体一共的个数12+22+32+42+52+62+72=140个;
没有涂上一点颜色的正方体12+22+32+42+52=55个.
答:(1)图中的正方体一共有14个.
(2)一点颜色都没涂上颜色的正方体有1个.
(3)72+62+52+42+32+22+12=140(个),
52+42+32+22+12=55(个).
故如果画家摆按此方式摆成七层,要140个正方体,同样涂上颜色,有55个正方体没有涂上一点颜色.
22.解:根据以上分析计算表面积=5+2×4+3+3×4+3×3+2×2+1=42cm2.
该图形的表面积为42cm2.
空间图形的初步认识》单元测试题
一.选择题
1.在长方形、长方体、三角形、球、直线、圆中,有( )个平面图形.
A.3
B.4
C.5
D.6
2.下列图形折叠起来不能做成一个开口的盒子的是( )
A.
B.
C.
D.
3.用一个平面去截一个长方体.截面的边数可能会出现的情况有( )
A.3种
B.4种
C.5种
D.6种
4.如图,在正方体中,AA1与AB,CC1,A1D1的关系分别是( )
A.垂直、平行、垂直
B.垂直、垂直、平行
C.垂直、平行、平行
D.以上都不对
5.一个正方体盒子的表面展开图如右所示,则这个纸盒的立体图形只能是( )
A.
B.
C.
D.
6.如图,每个长方体的六个面上分别写着1~6这六个数,并且任意两个相对的面上所写的两个数之和所写的两个数之和都等于7,靠在一起的长方体中,相连接两个面的数字之和等于8,图中打“?”的面上所写的数字是( )
A.3
B.5
C.2
D.1
7.如图,Rt△ABC中,若把Rt△ABC绕线斜边AB所在直线旋转一周,则所得的几何体为( )
A.两个三角形拼接成正方形
B.正方体
C.长方体
D.两个共底的圆锥
二.填空题
8.下图中几何体的截面分别是
、
、
.
9.直升机的螺旋桨转起来形成一个圆形的面,这说明了
.
10.下列图形(如图)可作为哪些行业的标志性图案,请把行业名称填在横线上
.
11.一个立方体的棱长为2cm,那么这个立方体的表面积为
cm2.
12.一个正方体的棱长之和是48,它的体积是
.
13.一个用硬纸板做成的长方体,至少要剪开
条棱,才能使它的表面展开.
14.5个正方体的六个面上分别写着1、2、3、4、5、6六个数,并且它们任意两个相对的面上所写的两个数的和都等于7.现在把五个这样的正方体一个挨着一个地连接起来(如图),在紧挨着的两个面上的两个数之和都等于8,那么,图中打“?”的这个面上所写的数是
.
15.根据下列多面体的平面展开图,填写多面体的名称:
(1)
,(2)
,(3)
.
三.解答题
16.如图所示,画一个长和宽分别为6cm、4cm的长方形,并将其按一定的方式进行旋转.
(1)你能得到几种不同的圆柱体?
(2)把一个平面图形旋转成几何体,必须明确哪两个条件?
17.如图所示,A、B、C、D、E五个城市,它们之间原有道路相通,现在打算在C、E两城市之间沿直线再修建一条公路,这条公路与原公路的交叉处必须设立交桥,问怎样确定立交桥的位置?应架设几座立交桥?
18.如图,四棱锥的底面ABCD为正方形,且PA=PB=PC=PD,现将其沿侧棱PA、PB、PC、PD剪开,并以底边为折线将其向外放到底面上,画出图形.
19.如图所示的是一个长方体的表面展开图,每个面上都标注了字母(字母朝外),回答下列问题:
(1)如果面A在长方体的底部放置,那么哪一个面会在它的上面?
(2)如果面F在前面,从左面看是面B,那么哪一个面会在上面?
(3)从右面看是面C,面E在左面,那么哪一个面会在上面?
20.图①中,A为正方体的顶点,在另一顶点B处有一昆虫.图②、图③是正方体的两个不同展开图,根据A、B位置的特点,请你在图②、图③中分别标出昆虫B的位置.
21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
22.如图,该物体是由14块棱长为1厘米的小正方体堆积而成的,求它的表面积.(含底面)
参考答案与试题解析
一.选择题
1.解:平面图形有长方形,三角形,直线,圆共4个,故选B.
2.解:由正方体及其表面展开图的特点可知,
A、B、D能折叠起来做成一只开口的盒子,不符合题意;
B折叠后有两面重合,不能做成一个开口的盒子,符合题意.
故选:B.
3.解:用一个平面去截一个长方体,截面可能为三角形、四边形、五边形、六边形共有四种情况,
故选:B.
4.解:根据以上分析知:AA1与AB,CC1,A1D1的关系分别是垂直、平行、垂直.故选A.
5.解:A、字母A与竖线应是平行的关系,故A错误;
B、展开后与原图形符合,故正确;
C、字母A与竖线应是平行的关系,故C错误;
D、原图形折叠不成D的形式,错误.
故选:B.
6.解:由题意可知:每个长方体的六个面上分别写着1~6这六个数,且任意两个相对的面上所写的两个数之和为7,可知第一个长方体所对应的1的对面为6,
又知靠在一起的长方体中,相连接两个面的数字之和等于8,可知下一个长方体的前面为2,以此类推,可得结果为3.
故选:A.
7.解:根据题意可知是两个共底的圆锥.
故选:D.
二.填空题
8.解:当截面平行于圆柱底面截取圆柱时得到截面图形是圆,截面截取经过四个顶点的截面时可以截得长方形,当截面垂直圆锥的底面时,截面图形是三角形.
9.解:直升机的螺旋桨可以近似看做线段,
由线动成面可得,转起来形成一个圆形的面,
故答案为:线动成面.
10.解:第一个很像工商银行的标志,第二个含有一个圆可作为科技的标志,第三个有三角板可作为教育的标志.
故答案为:银行、与科技有关的项目、与教育有关的项目.
11.解:这个立方体的表面积为:
6×22=6×4=24(cm2).
故答案为24.
12.解:∵正方体的棱有12条,棱长之和是48,
∴每一条棱长为48÷12=4,
∴它的体积是:4×4×4=64,
故答案为:64.
13.解:一个用硬纸板做成的长方体,至少要剪开7条棱,才能使它的表面展开.
故答案为:7.
14.解:由题意可知:正方体的六个面上分别写着1、2、3、4、5、6六个数,并且它们任意两个相对的面上所写的两个数的和都等于7,故第一个正方体的后面为5,在紧挨着的两个面上的两个数之和都等于8,则与它相接的第二个正方体的前面为3,对面为4,依此类推,即可求得结果为4.
故答案为4.
15.解:由平面展开图的特征可知,从左边第一个是长方体,第二个是三棱柱,第三个是三棱锥.
三.解答题
16.解:(1)由于长和宽分别为6cm、4cm的长方形,旋转可得到四种不同的圆柱体;
①一长方形的一条长AD(或BC)所在直线为旋转轴,旋转360°,可得到底面半径为4cm,高为6cm的圆柱体;
②一长方形的一条宽AB(或CD)所在直线为旋转轴,旋转一周,可得到底面半径为6cm,高为4cm的圆柱体;
③以长方形的长AD、BC的中点G、H所在直线为旋转轴,旋转180°,可得到底面半径为3cm,高为4cm的圆柱体;
④以长方形的长AB、DC的中点E、F所在直线为旋转轴,旋转180°,可得到底面半径为2cm,高为6cm的圆柱体;
(2)把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
17.解:连接CE,与BD的交点处架立交桥;1座.
18.解:
19.解:(1)根据“相间、Z端是对面”可知,
“A”与“F”相对,
“B”与“D”相对,
“C”与“E“相对,
所以面A在长方体的底部,那么F个面会在它的上面;
(2)若面F在前面,左面是面B,则“A”在后面,“D”在右面,此时“C”在上面,“E”在下面,或“E”在上面,“C”在下面,
答:如果面F在前面,从左面看是面B,那么“C”面或“E”面会在上面;
(3)从右面看是面C,面E在左面,则“B”面或“D”面在上面.
20.解:
21.解:(1)图中的正方体一共有1+4+9=14个;
(2)一点颜色都没涂上颜色的正方体有1个;
(3)七层的正方体一共的个数12+22+32+42+52+62+72=140个;
没有涂上一点颜色的正方体12+22+32+42+52=55个.
答:(1)图中的正方体一共有14个.
(2)一点颜色都没涂上颜色的正方体有1个.
(3)72+62+52+42+32+22+12=140(个),
52+42+32+22+12=55(个).
故如果画家摆按此方式摆成七层,要140个正方体,同样涂上颜色,有55个正方体没有涂上一点颜色.
22.解:根据以上分析计算表面积=5+2×4+3+3×4+3×3+2×2+1=42cm2.
该图形的表面积为42cm2.
