2020-2021学年沪教版七下数学期中基础练习(word版含案)
文档属性
| 名称 | 2020-2021学年沪教版七下数学期中基础练习(word版含案) |

|
|
| 格式 | zip | ||
| 文件大小 | 84.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览

文档简介
沪教版七下数学期中基础练习
一、选择题
在
到
的自然数中,其算术平方根是有理数的共有
A.
个
B.
个
C.
个
D.
个
下列实数中,是无理数的为
A.
B.
C.
D.
如果
和
是正实数
的两个不同的平方根,那么
的值为
A.
B.
C.
D.
如果一个角的两边分别平行于另一个角的两边,则这两个角
A.相等
B.互补
C.相等或互补
D.关系不确定
如图,下列说法中正确的是
A.
与
是同位角
B.
与
是同旁内角
C.
与
是内错角
D.
与
是内错角
中,已知
,,则
可以是
A.
B.
C.
D.
二、填空题
如果
的平方根是
,那么
.
如果
有意义,
的取值范围是
.
数轴上点
表示
,那么与点
相距
个长度单位的点所表示的数是
.
的整数部分是
,小数部分是
.
近似数
精确到
位;有效数字是
.
若等腰三角形的顶角为
,则它的底角度数为
.
如果
与
互为补角,,
,若
,则
的补角为
.
如图,
平分
,
平分
,则与
互余的角有
.
若一个三角形的三个外角的度数之比为
,则与之相应的
个内角的度数之比为
.
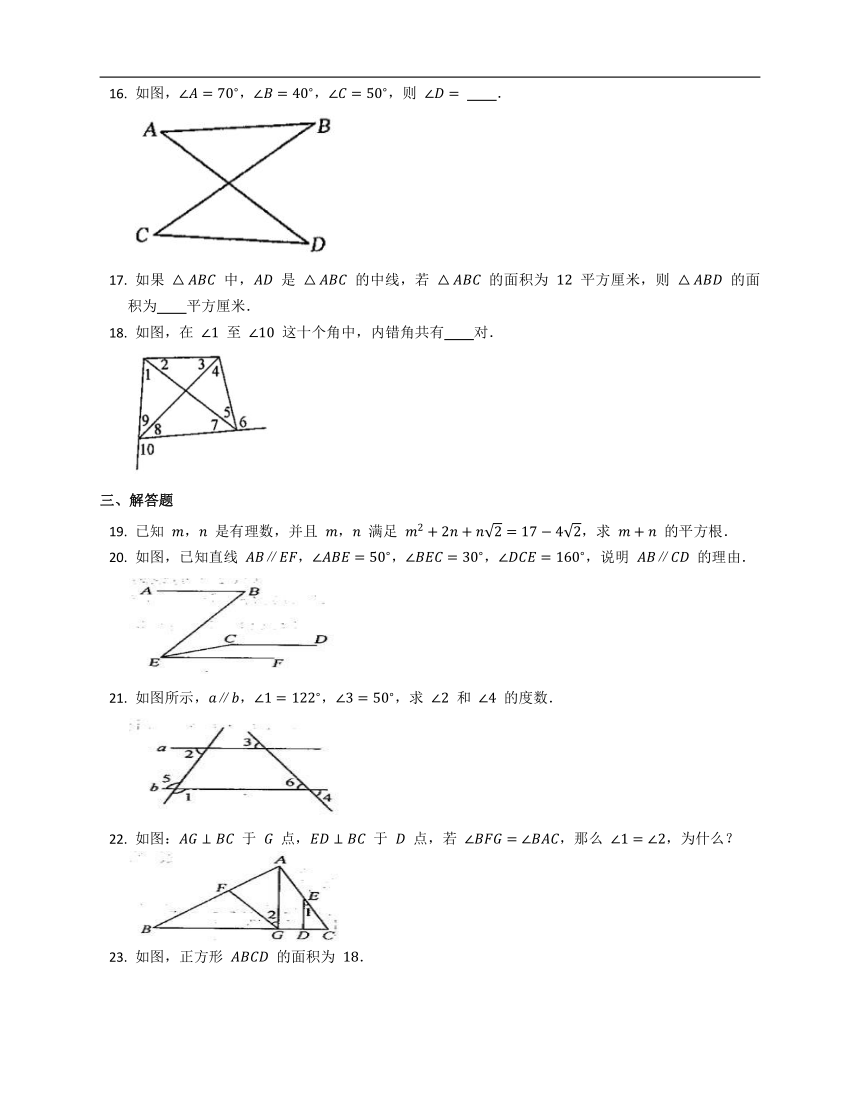
如图,,,,则
.
如果
中,
是
的中线,若
的面积为
平方厘米,则
的面积为
平方厘米.
如图,在
至
这十个角中,内错角共有
对.
三、解答题
已知
,
是有理数,并且
,
满足
,求
的平方根.
如图,已知直线
,,,,说明
的理由.
如图所示,,,,求
和
的度数.
如图:
于
点,
于
点,若
,那么
,为什么?
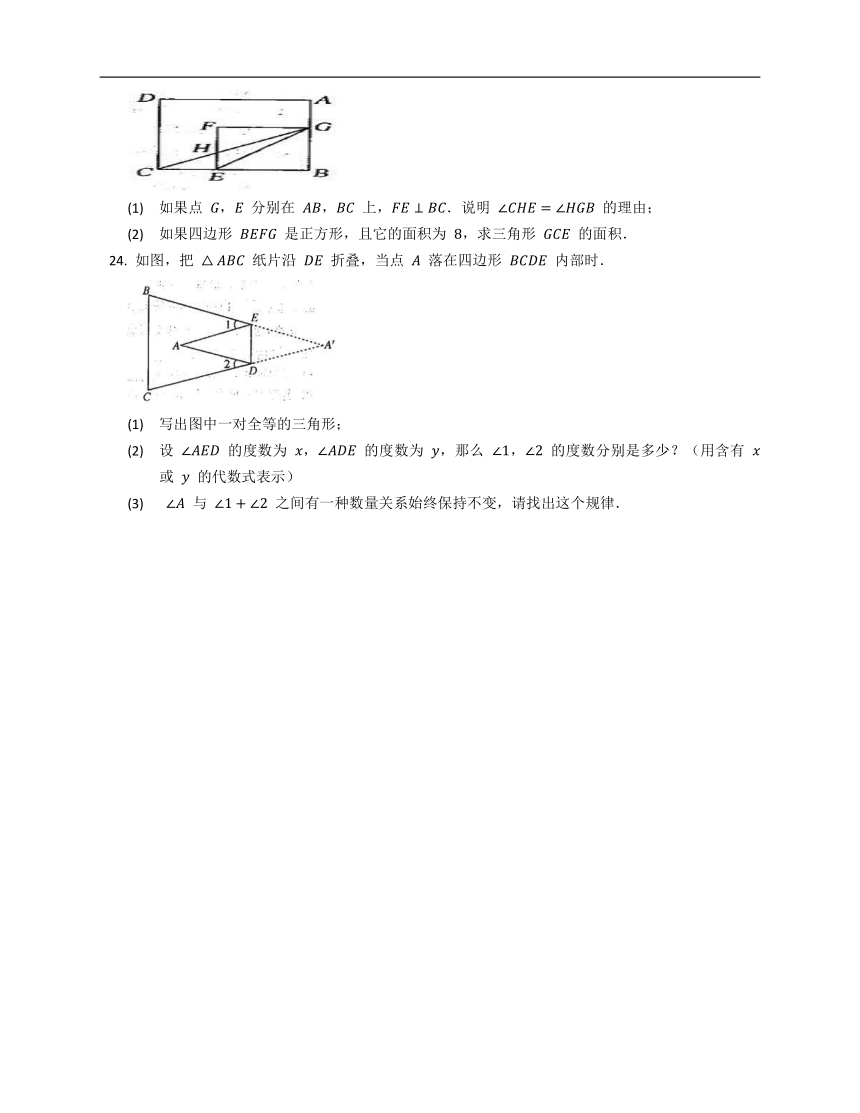
如图,正方形
的面积为
.
(1)
如果点
,
分别在
,
上,.说明
的理由;
(2)
如果四边形
是正方形,且它的面积为
,求三角形
的面积.
如图,把
纸片沿
折叠,当点
落在四边形
内部时.
(1)
写出图中一对全等的三角形;
(2)
设
的度数为
,
的度数为
,那么
,
的度数分别是多少?(用含有
或
的代数式表示)
(3)
与
之间有一种数量关系始终保持不变,请找出这个规律.
答案
一、选择题
1.
【答案】B
2.
【答案】C
3.
【答案】D
4.
【答案】C
5.
【答案】B
6.
【答案】C
二、填空题
7.
【答案】
8.
【答案】
9.
【答案】
或
10.
【答案】
;
11.
【答案】千;
,
12.
【答案】
13.
【答案】
;
14.
【答案】
,
15.
【答案】
16.
【答案】
17.
【答案】
18.
【答案】
三、解答题
19.
【答案】由题意可得
即
当
时,,
所以
没有平方根;
当
时,,
所以
的平方根是
.
综上所述,
的平方根是
.
20.
【答案】
(已知),
(两直线平行,内错角相等),
(已知),
(等量代换),
(角的和差),(已知),
(等式性质),
(已知),
(等式性质),
(同旁内角互补,两直线平行),
(已知),
(平行的传递性).
21.
【答案】
(对顶角相等),且
(已知),
(两直线平行,同旁内角互补),
(两直线平行,同位角相等),
(对顶角相等).
22.
【答案】
,(已知),
(垂直的意义),
(同位角相等,两直线平行),
(两直线平行,同位角相等),
(已知),
(同位角相等,两直线平行),
(两直线平行,内错角相等),
(等量代换).
23.
【答案】
(1)
四边形
是正方形(已知),
(正方形每个内角都等于
),
(已知),
(垂直的意义),
(等量代换),
(同位角相等,两直线平行),
(两直线平行,同位角相等).
(2)
(已知),
,
同理
,
(线段的和差),
(三角形面积公式),
(等式性质).
24.
【答案】
(1)
.
(2)
折叠,
,,
,.
(3)
,,
,,
,即
.
一、选择题
在
到
的自然数中,其算术平方根是有理数的共有
A.
个
B.
个
C.
个
D.
个
下列实数中,是无理数的为
A.
B.
C.
D.
如果
和
是正实数
的两个不同的平方根,那么
的值为
A.
B.
C.
D.
如果一个角的两边分别平行于另一个角的两边,则这两个角
A.相等
B.互补
C.相等或互补
D.关系不确定
如图,下列说法中正确的是
A.
与
是同位角
B.
与
是同旁内角
C.
与
是内错角
D.
与
是内错角
中,已知
,,则
可以是
A.
B.
C.
D.
二、填空题
如果
的平方根是
,那么
.
如果
有意义,
的取值范围是
.
数轴上点
表示
,那么与点
相距
个长度单位的点所表示的数是
.
的整数部分是
,小数部分是
.
近似数
精确到
位;有效数字是
.
若等腰三角形的顶角为
,则它的底角度数为
.
如果
与
互为补角,,
,若
,则
的补角为
.
如图,
平分
,
平分
,则与
互余的角有
.
若一个三角形的三个外角的度数之比为
,则与之相应的
个内角的度数之比为
.
如图,,,,则
.
如果
中,
是
的中线,若
的面积为
平方厘米,则
的面积为
平方厘米.
如图,在
至
这十个角中,内错角共有
对.
三、解答题
已知
,
是有理数,并且
,
满足
,求
的平方根.
如图,已知直线
,,,,说明
的理由.
如图所示,,,,求
和
的度数.
如图:
于
点,
于
点,若
,那么
,为什么?
如图,正方形
的面积为
.
(1)
如果点
,
分别在
,
上,.说明
的理由;
(2)
如果四边形
是正方形,且它的面积为
,求三角形
的面积.
如图,把
纸片沿
折叠,当点
落在四边形
内部时.
(1)
写出图中一对全等的三角形;
(2)
设
的度数为
,
的度数为
,那么
,
的度数分别是多少?(用含有
或
的代数式表示)
(3)
与
之间有一种数量关系始终保持不变,请找出这个规律.
答案
一、选择题
1.
【答案】B
2.
【答案】C
3.
【答案】D
4.
【答案】C
5.
【答案】B
6.
【答案】C
二、填空题
7.
【答案】
8.
【答案】
9.
【答案】
或
10.
【答案】
;
11.
【答案】千;
,
12.
【答案】
13.
【答案】
;
14.
【答案】
,
15.
【答案】
16.
【答案】
17.
【答案】
18.
【答案】
三、解答题
19.
【答案】由题意可得
即
当
时,,
所以
没有平方根;
当
时,,
所以
的平方根是
.
综上所述,
的平方根是
.
20.
【答案】
(已知),
(两直线平行,内错角相等),
(已知),
(等量代换),
(角的和差),(已知),
(等式性质),
(已知),
(等式性质),
(同旁内角互补,两直线平行),
(已知),
(平行的传递性).
21.
【答案】
(对顶角相等),且
(已知),
(两直线平行,同旁内角互补),
(两直线平行,同位角相等),
(对顶角相等).
22.
【答案】
,(已知),
(垂直的意义),
(同位角相等,两直线平行),
(两直线平行,同位角相等),
(已知),
(同位角相等,两直线平行),
(两直线平行,内错角相等),
(等量代换).
23.
【答案】
(1)
四边形
是正方形(已知),
(正方形每个内角都等于
),
(已知),
(垂直的意义),
(等量代换),
(同位角相等,两直线平行),
(两直线平行,同位角相等).
(2)
(已知),
,
同理
,
(线段的和差),
(三角形面积公式),
(等式性质).
24.
【答案】
(1)
.
(2)
折叠,
,,
,.
(3)
,,
,,
,即
.
同课章节目录
