人教版数学八年级下册:20.1.2 中位数和众数 同步练习试卷(Word版附答案)
文档属性
| 名称 | 人教版数学八年级下册:20.1.2 中位数和众数 同步练习试卷(Word版附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 265.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 07:25:00 | ||
图片预览




文档简介
20.1.2 中位数和众数
第1课时 中位数和众数
1.一组数据2,4,3,5,2的中位数是( )
A.5 B.3.5 C.3 D.2.5
2.某校10名篮球运动员的年龄情况,统计如下表:
年龄(岁)
12
13
14
15
人数(名)
2
4
3
1
则这10名篮球运动员年龄的中位数为( )
A.12 B.13 C.13.5 D.14
3.已知一组从小到大排列的数据0,4,x,10的中位数是5,则x= .
4.已知遵义市某天六个整点时的气温绘制成的统计图如下图,则这六个整点时气温的中位数是 ℃.
5.在某公益活动中,张益明对本班同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是 元.
6.某校对八年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):4,4,3.5,5,5,4,这组数据的众数是( )
A.4 B.3.5 C.5 D.3
7.某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某一天每个工人的生产件数,获得数据如下表:
生产件数(件)
10
11
12
13
14
15
人数(人)
1
5
4
3
2
1
则这一天16名工人生产件数的众数是( )
A.5件 B.11件 C.12件 D.15件
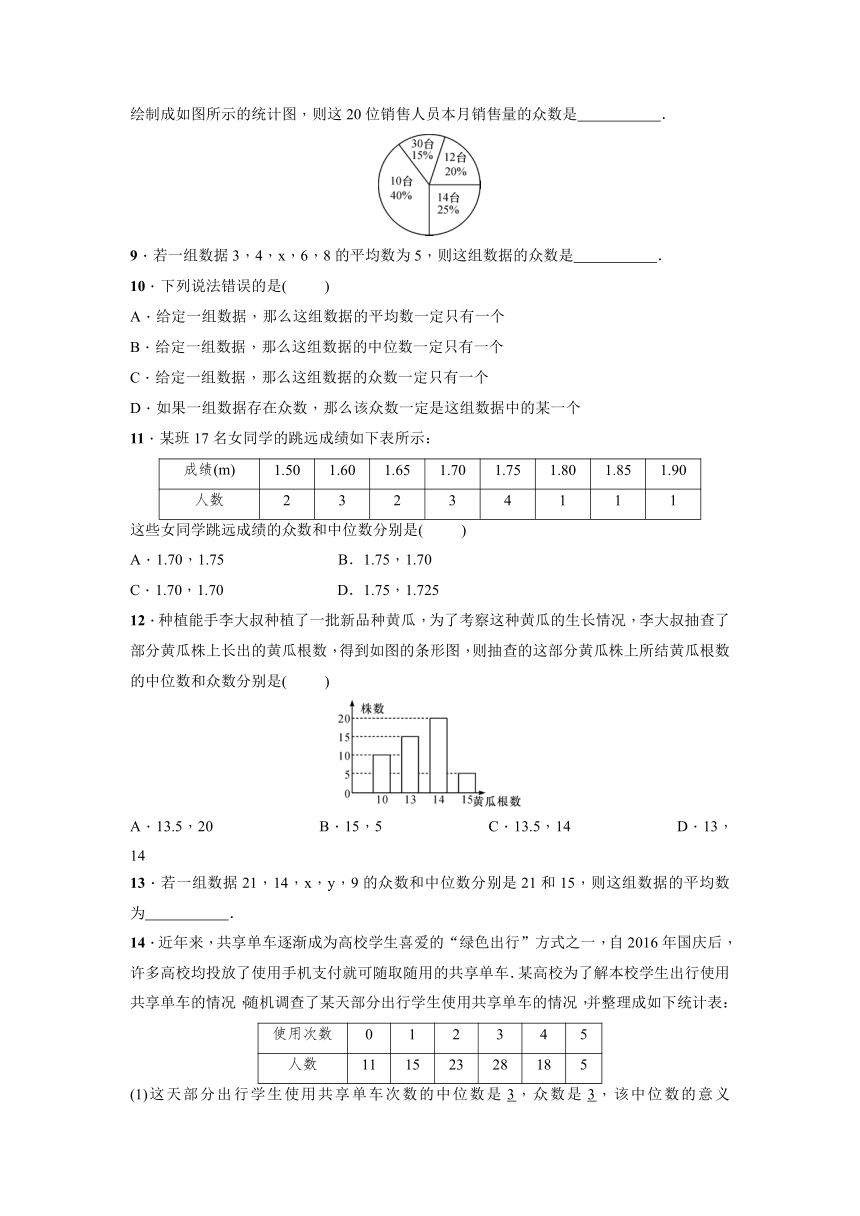
8.某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的众数是 .
9.若一组数据3,4,x,6,8的平均数为5,则这组数据的众数是 .
10.下列说法错误的是( )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
11.某班17名女同学的跳远成绩如下表所示:
成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
这些女同学跳远成绩的众数和中位数分别是( )
A.1.70,1.75 B.1.75,1.70
C.1.70,1.70 D.1.75,1.725
12.种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( )
A.13.5,20 B.15,5 C.13.5,14 D.13,14
13.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .
14.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表:
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是3,众数是3,该中位数的意义是 ;
(2)若该校某天有1 500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
15.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图1中m的值为 ;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
16.为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下:
收集数据:
90 91 89 96 90 98 90 97 91 98 99
97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整;
整理、描述数据:
成绩/分
88
89
90
91
95
96
97
98
99
学生人数
2
1
5
3
2
1
3
2
1
数据分析:样本数据的平均数、众数和中位数如下表:
平均数
众数
中位数
93
90
91
得出结论:
(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为 分;
数据应用:
(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
第2课时 平均数、中位数和众数的应用
1.某学校九年级1班九名同学参加定点投篮测试,每人投篮六次,投中的次数统计如下:4,3,5,5,2,5,3,4,1,这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
2.小亮家1月至10月的用电量统计如图所示,这组数据的众数和中位数分别是( )
A.30和 20 B.30和25 C.30和22.5 D.30和17.5
3.某共享单车前a千米1元,超过a千米的,每千米2元.若要使使用该共享单车50%的人只花1元钱,a应该要取什么数( )
A.平均数 B.中位数 C.众数 D.以上都可以
4.某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋的销量如下表所示:
尺码/厘米
22.5
23
23.5
24
24.5
销售量/双
35
40
30
17
8
通过分析上述数据,对鞋店业主的进货最有意义的是 .
5.某校举办“成语听写大赛”,15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是 .(填“平均数”或“中位数”或“众数”)
6.某公司共25名员工,下表是他们月收入的资料.
月收
入/元
45 000
18 000
10 000
5 500
4 800
3 400
3 000
2 200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是 元,众数是 元;
(2)根据上表,可以算得该公司员工月收入的平均数为6 276元,你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
7.公园里有甲、乙两队游客在做团体游戏,两队游客的年龄如下(单位:岁):
甲队:13,13,14,15,15,15,15,16,17,17;
乙队:5,6,6,7,7,8,8,8,46,49.
(1)分别算出两队游客年龄的平均数、众数和中位数;
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
8.“五四”青年节期间,某团委举办了“我的中国梦”演讲知识竞赛,并将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些参加演讲的同学的中位数和平均数分别是( )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
9.王老师是一名快走锻炼爱好者,他用手机软件连续记录了某月16天每天快走锻炼的步数(单位:万步),并将记录的结果绘制成如图所示的条形统计图,则他每天所走步数的中位数是 万步,众数是 万步.
10.某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数为2 500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员,请你回答图中小王的问题,并指出用(2)中的哪个数据向小王介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.
11.为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升).
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
参考答案:
20.1.2 中位数和众数
第1课时 中位数和众数
1.一组数据2,4,3,5,2的中位数是( C )
A.5 B.3.5 C.3 D.2.5
2.某校10名篮球运动员的年龄情况,统计如下表:
年龄(岁)
12
13
14
15
人数(名)
2
4
3
1
则这10名篮球运动员年龄的中位数为( B )
A.12 B.13 C.13.5 D.14
3.已知一组从小到大排列的数据0,4,x,10的中位数是5,则x=6.
4.已知遵义市某天六个整点时的气温绘制成的统计图如下图,则这六个整点时气温的中位数是24.5℃.
5.在某公益活动中,张益明对本班同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是20元.
6.某校对八年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):4,4,3.5,5,5,4,这组数据的众数是( A )
A.4 B.3.5 C.5 D.3
7.某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某一天每个工人的生产件数,获得数据如下表:
生产件数(件)
10
11
12
13
14
15
人数(人)
1
5
4
3
2
1
则这一天16名工人生产件数的众数是( B )
A.5件 B.11件 C.12件 D.15件
8.某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的众数是10.
9.若一组数据3,4,x,6,8的平均数为5,则这组数据的众数是4.
10.下列说法错误的是( C )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
11.某班17名女同学的跳远成绩如下表所示:
成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
这些女同学跳远成绩的众数和中位数分别是( B )
A.1.70,1.75 B.1.75,1.70 C.1.70,1.70 D.1.75,1.725
12.种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( C )
A.13.5,20 B.15,5 C.13.5,14 D.13,14
13.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为16.
14.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表:
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是3,众数是3,该中位数的意义是表示这部分出行学生在这天约有一半人使用共享单车的次数在3次以上(含3次);
(2)若该校某天有1 500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
解:1 500×=765(人).
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
15.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为40,图1中m的值为15;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
解:(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为=36.
(3)200×30%=60(双).
答:建议购买35号运动鞋60双.
16.为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下:
收集数据:
90 91 89 96 90 98 90 97 91 98 99
97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整;
整理、描述数据:
成绩/分
88
89
90
91
95
96
97
98
99
学生人数
2
1
5
3
2
1
3
2
1
数据分析:样本数据的平均数、众数和中位数如下表:
平均数
众数
中位数
93
90
91
得出结论:
(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为91分;
数据应用:
(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
解:估计评选该荣誉称号的最低分数为97分.理由如下:
∵20×30%=6(人),
∴估计评选该荣誉称号的最低分数为97分.
第2课时 平均数、中位数和众数的应用
1.某学校九年级1班九名同学参加定点投篮测试,每人投篮六次,投中的次数统计如下:4,3,5,5,2,5,3,4,1,这组数据的中位数,众数分别为( A )
A.4,5 B.5,4 C.4,4 D.5,5
2.小亮家1月至10月的用电量统计如图所示,这组数据的众数和中位数分别是( C )
A.30和 20 B.30和25 C.30和22.5 D.30和17.5
3.某共享单车前a千米1元,超过a千米的,每千米2元.若要使使用该共享单车50%的人只花1元钱,a应该要取什么数( B )
A.平均数 B.中位数 C.众数 D.以上都可以
4.某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋的销量如下表所示:
尺码/厘米
22.5
23
23.5
24
24.5
销售量/双
35
40
30
17
8
通过分析上述数据,对鞋店业主的进货最有意义的是众数.
5.某校举办“成语听写大赛”,15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数.(填“平均数”或“中位数”或“众数”)
6.某公司共25名员工,下表是他们月收入的资料.
月收
入/元
45 000
18 000
10 000
5 500
4 800
3 400
3 000
2 200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是3_400元,众数是3_000元;
(2)根据上表,可以算得该公司员工月收入的平均数为6 276元,你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
解:本题答案不唯一,如:用中位数反映该公司全体员工月收入水平较为合适.在这组数据中有差异较大的数据,这会导致平均数较大.该公司员工月收入的中位数是3 400元,这说明除去月收入为3 400元的员工,一半员工收入高于3 400元,另一半员工收入低于3 400元.因此,利用中位数可以更好地反映这组数据的集中趋势.
7.公园里有甲、乙两队游客在做团体游戏,两队游客的年龄如下(单位:岁):
甲队:13,13,14,15,15,15,15,16,17,17;
乙队:5,6,6,7,7,8,8,8,46,49.
(1)分别算出两队游客年龄的平均数、众数和中位数;
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
解:(1)甲队游客年龄的平均数为×(13+13+14+15+15+15+15+16+17+17)=15(岁),众数为15岁,中位数为15岁.
乙队游客年龄的平均数为×(5+6+6+7+7+8+8+8+46+49)=15(岁),众数为8岁,中数为7.5岁.
(2)甲队游客年龄的平均数能代表他们的年龄特征,乙队游客年龄的平均数不能代表他们的年龄特征,对于乙队游客而言,10人中有8人的年龄在9岁以下,而说他们的平均年龄是15岁,会让人误认为这队游客的年龄都在15岁左右,所以乙队的平均数不能代表该队游客年龄的特征.可选用中位数或众数来代表乙队游客的年龄特征.
8.“五四”青年节期间,某团委举办了“我的中国梦”演讲知识竞赛,并将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些参加演讲的同学的中位数和平均数分别是( D )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
9.王老师是一名快走锻炼爱好者,他用手机软件连续记录了某月16天每天快走锻炼的步数(单位:万步),并将记录的结果绘制成如图所示的条形统计图,则他每天所走步数的中位数是1.1万步,众数是1.2万步.
10.某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有16名;
(2)所有员工月工资的平均数为2 500元,中位数为1_700元,众数为1_600元;
(3)小张到这家公司应聘普通工作人员,请你回答图中小王的问题,并指出用(2)中的哪个数据向小王介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.
解:(3)这个老板的介绍不能反映该公司员工的月工资实际水平,用中位数或众数来介绍更合理些.
(4)y=≈1 713(元),
y能反映该公司员工的月工资实际水平.
11.为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升).
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
解:(1)这7天内小申家每天用水量的平均数为=800(升),
将这7天的用水量从小到大重新排列为780,785,790,800,805,815,825,
∴用水量的中位数为800升.
(2)×100%=12.5%,
答:第3天小申家洗衣服的水占这一天总用水量的百分比为12.5%.
(3)小申家冲厕所的用水量较大,可以将洗衣服的水留到冲厕所,
采用以上建议,每天可节约用水100升,一个月估计可以节约用水100×30=3 000(升).
第1课时 中位数和众数
1.一组数据2,4,3,5,2的中位数是( )
A.5 B.3.5 C.3 D.2.5
2.某校10名篮球运动员的年龄情况,统计如下表:
年龄(岁)
12
13
14
15
人数(名)
2
4
3
1
则这10名篮球运动员年龄的中位数为( )
A.12 B.13 C.13.5 D.14
3.已知一组从小到大排列的数据0,4,x,10的中位数是5,则x= .
4.已知遵义市某天六个整点时的气温绘制成的统计图如下图,则这六个整点时气温的中位数是 ℃.
5.在某公益活动中,张益明对本班同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是 元.
6.某校对八年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):4,4,3.5,5,5,4,这组数据的众数是( )
A.4 B.3.5 C.5 D.3
7.某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某一天每个工人的生产件数,获得数据如下表:
生产件数(件)
10
11
12
13
14
15
人数(人)
1
5
4
3
2
1
则这一天16名工人生产件数的众数是( )
A.5件 B.11件 C.12件 D.15件
8.某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的众数是 .
9.若一组数据3,4,x,6,8的平均数为5,则这组数据的众数是 .
10.下列说法错误的是( )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
11.某班17名女同学的跳远成绩如下表所示:
成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
这些女同学跳远成绩的众数和中位数分别是( )
A.1.70,1.75 B.1.75,1.70
C.1.70,1.70 D.1.75,1.725
12.种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( )
A.13.5,20 B.15,5 C.13.5,14 D.13,14
13.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .
14.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表:
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是3,众数是3,该中位数的意义是 ;
(2)若该校某天有1 500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
15.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图1中m的值为 ;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
16.为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下:
收集数据:
90 91 89 96 90 98 90 97 91 98 99
97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整;
整理、描述数据:
成绩/分
88
89
90
91
95
96
97
98
99
学生人数
2
1
5
3
2
1
3
2
1
数据分析:样本数据的平均数、众数和中位数如下表:
平均数
众数
中位数
93
90
91
得出结论:
(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为 分;
数据应用:
(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
第2课时 平均数、中位数和众数的应用
1.某学校九年级1班九名同学参加定点投篮测试,每人投篮六次,投中的次数统计如下:4,3,5,5,2,5,3,4,1,这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
2.小亮家1月至10月的用电量统计如图所示,这组数据的众数和中位数分别是( )
A.30和 20 B.30和25 C.30和22.5 D.30和17.5
3.某共享单车前a千米1元,超过a千米的,每千米2元.若要使使用该共享单车50%的人只花1元钱,a应该要取什么数( )
A.平均数 B.中位数 C.众数 D.以上都可以
4.某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋的销量如下表所示:
尺码/厘米
22.5
23
23.5
24
24.5
销售量/双
35
40
30
17
8
通过分析上述数据,对鞋店业主的进货最有意义的是 .
5.某校举办“成语听写大赛”,15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是 .(填“平均数”或“中位数”或“众数”)
6.某公司共25名员工,下表是他们月收入的资料.
月收
入/元
45 000
18 000
10 000
5 500
4 800
3 400
3 000
2 200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是 元,众数是 元;
(2)根据上表,可以算得该公司员工月收入的平均数为6 276元,你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
7.公园里有甲、乙两队游客在做团体游戏,两队游客的年龄如下(单位:岁):
甲队:13,13,14,15,15,15,15,16,17,17;
乙队:5,6,6,7,7,8,8,8,46,49.
(1)分别算出两队游客年龄的平均数、众数和中位数;
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
8.“五四”青年节期间,某团委举办了“我的中国梦”演讲知识竞赛,并将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些参加演讲的同学的中位数和平均数分别是( )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
9.王老师是一名快走锻炼爱好者,他用手机软件连续记录了某月16天每天快走锻炼的步数(单位:万步),并将记录的结果绘制成如图所示的条形统计图,则他每天所走步数的中位数是 万步,众数是 万步.
10.某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数为2 500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员,请你回答图中小王的问题,并指出用(2)中的哪个数据向小王介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.
11.为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升).
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
参考答案:
20.1.2 中位数和众数
第1课时 中位数和众数
1.一组数据2,4,3,5,2的中位数是( C )
A.5 B.3.5 C.3 D.2.5
2.某校10名篮球运动员的年龄情况,统计如下表:
年龄(岁)
12
13
14
15
人数(名)
2
4
3
1
则这10名篮球运动员年龄的中位数为( B )
A.12 B.13 C.13.5 D.14
3.已知一组从小到大排列的数据0,4,x,10的中位数是5,则x=6.
4.已知遵义市某天六个整点时的气温绘制成的统计图如下图,则这六个整点时气温的中位数是24.5℃.
5.在某公益活动中,张益明对本班同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是20元.
6.某校对八年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):4,4,3.5,5,5,4,这组数据的众数是( A )
A.4 B.3.5 C.5 D.3
7.某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某一天每个工人的生产件数,获得数据如下表:
生产件数(件)
10
11
12
13
14
15
人数(人)
1
5
4
3
2
1
则这一天16名工人生产件数的众数是( B )
A.5件 B.11件 C.12件 D.15件
8.某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的众数是10.
9.若一组数据3,4,x,6,8的平均数为5,则这组数据的众数是4.
10.下列说法错误的是( C )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
11.某班17名女同学的跳远成绩如下表所示:
成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
这些女同学跳远成绩的众数和中位数分别是( B )
A.1.70,1.75 B.1.75,1.70 C.1.70,1.70 D.1.75,1.725
12.种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( C )
A.13.5,20 B.15,5 C.13.5,14 D.13,14
13.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为16.
14.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表:
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)这天部分出行学生使用共享单车次数的中位数是3,众数是3,该中位数的意义是表示这部分出行学生在这天约有一半人使用共享单车的次数在3次以上(含3次);
(2)若该校某天有1 500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
解:1 500×=765(人).
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
15.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为40,图1中m的值为15;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
解:(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为=36.
(3)200×30%=60(双).
答:建议购买35号运动鞋60双.
16.为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下:
收集数据:
90 91 89 96 90 98 90 97 91 98 99
97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整;
整理、描述数据:
成绩/分
88
89
90
91
95
96
97
98
99
学生人数
2
1
5
3
2
1
3
2
1
数据分析:样本数据的平均数、众数和中位数如下表:
平均数
众数
中位数
93
90
91
得出结论:
(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为91分;
数据应用:
(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
解:估计评选该荣誉称号的最低分数为97分.理由如下:
∵20×30%=6(人),
∴估计评选该荣誉称号的最低分数为97分.
第2课时 平均数、中位数和众数的应用
1.某学校九年级1班九名同学参加定点投篮测试,每人投篮六次,投中的次数统计如下:4,3,5,5,2,5,3,4,1,这组数据的中位数,众数分别为( A )
A.4,5 B.5,4 C.4,4 D.5,5
2.小亮家1月至10月的用电量统计如图所示,这组数据的众数和中位数分别是( C )
A.30和 20 B.30和25 C.30和22.5 D.30和17.5
3.某共享单车前a千米1元,超过a千米的,每千米2元.若要使使用该共享单车50%的人只花1元钱,a应该要取什么数( B )
A.平均数 B.中位数 C.众数 D.以上都可以
4.某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋的销量如下表所示:
尺码/厘米
22.5
23
23.5
24
24.5
销售量/双
35
40
30
17
8
通过分析上述数据,对鞋店业主的进货最有意义的是众数.
5.某校举办“成语听写大赛”,15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数.(填“平均数”或“中位数”或“众数”)
6.某公司共25名员工,下表是他们月收入的资料.
月收
入/元
45 000
18 000
10 000
5 500
4 800
3 400
3 000
2 200
人数
1
1
1
3
6
1
11
1
(1)该公司员工月收入的中位数是3_400元,众数是3_000元;
(2)根据上表,可以算得该公司员工月收入的平均数为6 276元,你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
解:本题答案不唯一,如:用中位数反映该公司全体员工月收入水平较为合适.在这组数据中有差异较大的数据,这会导致平均数较大.该公司员工月收入的中位数是3 400元,这说明除去月收入为3 400元的员工,一半员工收入高于3 400元,另一半员工收入低于3 400元.因此,利用中位数可以更好地反映这组数据的集中趋势.
7.公园里有甲、乙两队游客在做团体游戏,两队游客的年龄如下(单位:岁):
甲队:13,13,14,15,15,15,15,16,17,17;
乙队:5,6,6,7,7,8,8,8,46,49.
(1)分别算出两队游客年龄的平均数、众数和中位数;
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
解:(1)甲队游客年龄的平均数为×(13+13+14+15+15+15+15+16+17+17)=15(岁),众数为15岁,中位数为15岁.
乙队游客年龄的平均数为×(5+6+6+7+7+8+8+8+46+49)=15(岁),众数为8岁,中数为7.5岁.
(2)甲队游客年龄的平均数能代表他们的年龄特征,乙队游客年龄的平均数不能代表他们的年龄特征,对于乙队游客而言,10人中有8人的年龄在9岁以下,而说他们的平均年龄是15岁,会让人误认为这队游客的年龄都在15岁左右,所以乙队的平均数不能代表该队游客年龄的特征.可选用中位数或众数来代表乙队游客的年龄特征.
8.“五四”青年节期间,某团委举办了“我的中国梦”演讲知识竞赛,并将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些参加演讲的同学的中位数和平均数分别是( D )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
9.王老师是一名快走锻炼爱好者,他用手机软件连续记录了某月16天每天快走锻炼的步数(单位:万步),并将记录的结果绘制成如图所示的条形统计图,则他每天所走步数的中位数是1.1万步,众数是1.2万步.
10.某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有16名;
(2)所有员工月工资的平均数为2 500元,中位数为1_700元,众数为1_600元;
(3)小张到这家公司应聘普通工作人员,请你回答图中小王的问题,并指出用(2)中的哪个数据向小王介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.
解:(3)这个老板的介绍不能反映该公司员工的月工资实际水平,用中位数或众数来介绍更合理些.
(4)y=≈1 713(元),
y能反映该公司员工的月工资实际水平.
11.为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升).
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
解:(1)这7天内小申家每天用水量的平均数为=800(升),
将这7天的用水量从小到大重新排列为780,785,790,800,805,815,825,
∴用水量的中位数为800升.
(2)×100%=12.5%,
答:第3天小申家洗衣服的水占这一天总用水量的百分比为12.5%.
(3)小申家冲厕所的用水量较大,可以将洗衣服的水留到冲厕所,
采用以上建议,每天可节约用水100升,一个月估计可以节约用水100×30=3 000(升).
