人教版数学八年级下册:19.2.3 一次函数与方程、不等式 同步练习试卷(Word版附答案)
文档属性
| 名称 | 人教版数学八年级下册:19.2.3 一次函数与方程、不等式 同步练习试卷(Word版附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 07:29:57 | ||
图片预览


文档简介
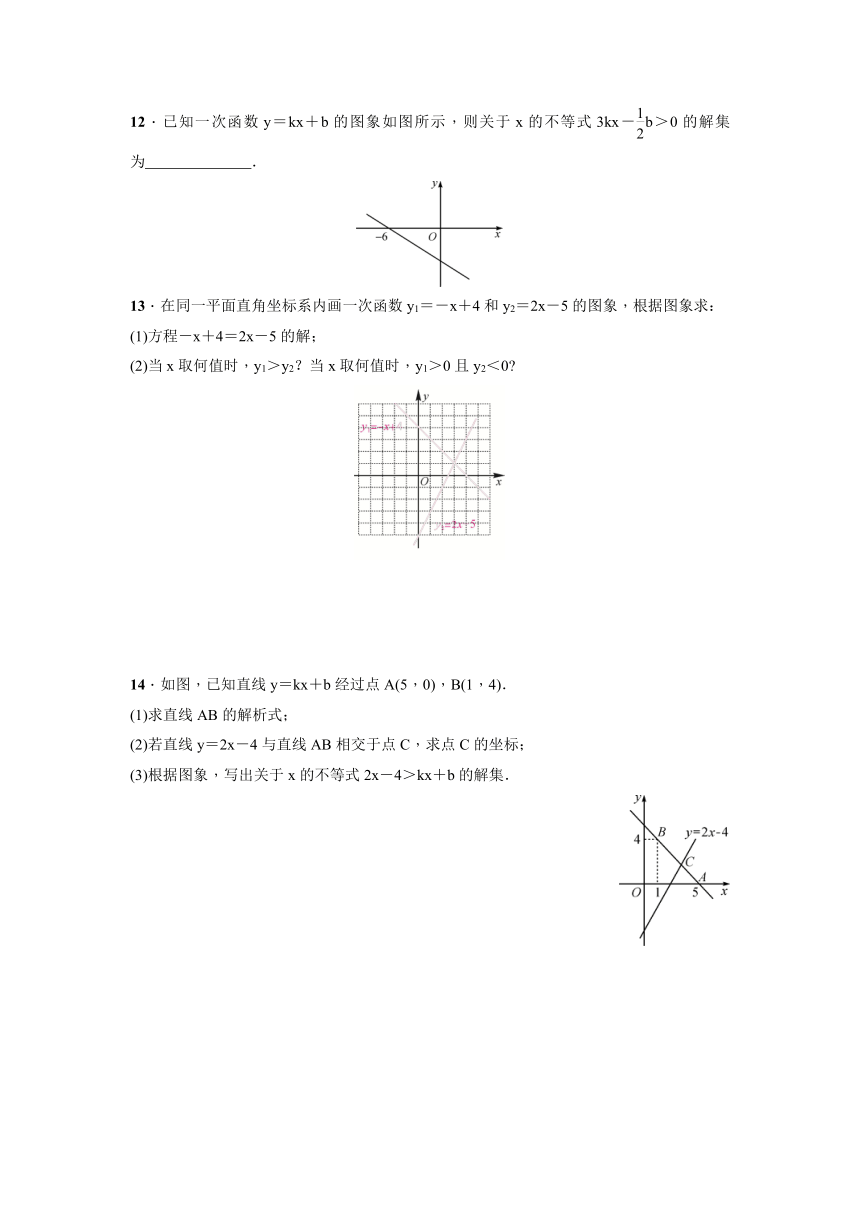
19.2.3 一次函数与方程、不等式
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( )
A.1 B.2 C.3 D.4
2.若方程ax+b=0的解是x=-2,则图中一定不是直线y=ax+b的是( )
A B C D
3.如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4).结合图象可知,关于x的方程ax+b=0的解是 .
4.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
21043906223005.如图所示,直线l1:y=x+6与直线l2:y=-x-2交于点P(-2,3),则不等式x+6>-x-2的解集是( )
A.x>-2
B.x≥-2
C.x<-2
D.x≤-2
6.如图所示,一次函数y=ax+b(a,b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为 .
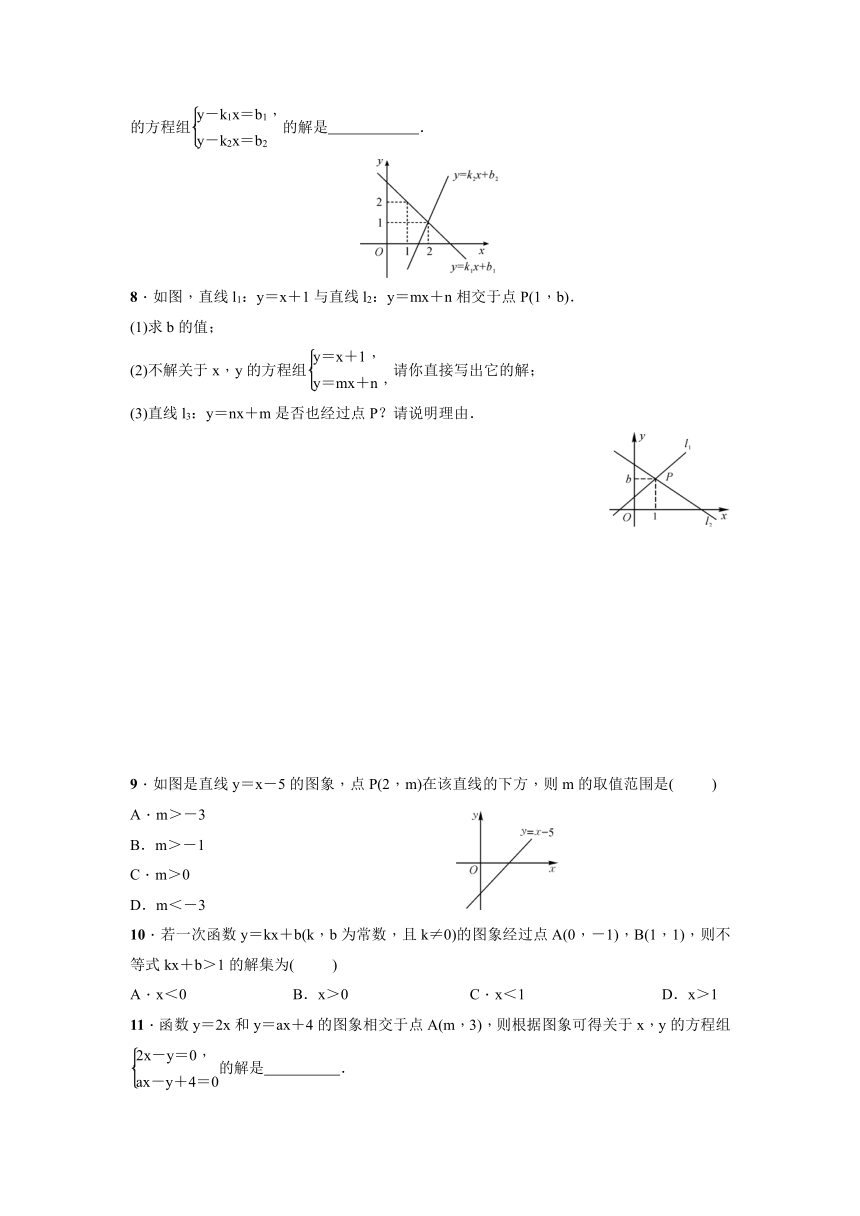
7.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 .
8.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
9.如图是直线y=x-5的图象,点P(2,m)在该直线的下方,则m的取值范围是( )
286639053340A.m>-3
B.m>-1
C.m>0
D.m<-3
10.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.x<0 B.x>0 C.x<1 D.x>1
11.函数y=2x和y=ax+4的图象相交于点A(m,3),则根据图象可得关于x,y的方程组的解是 .
12.已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为 .
13.在同一平面直角坐标系内画一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
(1)方程-x+4=2x-5的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
14.如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4>kx+b的解集.
15.A,B两地相距60 km,甲、乙两人分别从两地出发相向而行,甲先出发.如图,l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是l2(填“l1”或“l2”);甲的速度是 km/h,乙的速度是 km/h;
(2)甲出发多少小时时,两人恰好相距5 km?
参考答案:
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( A )
A.1 B.2 C.3 D.4
2.若方程ax+b=0的解是x=-2,则图中一定不是直线y=ax+b的是( B )
A B C D
3.如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4).结合图象可知,关于x的方程ax+b=0的解是x=2.
4.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( B )
A.x>2 B.x<2 C.x≥2 D.x≤2
5.如图所示,直线l1:y=x+6与直线l2:y=-x-2交于点P(-2,3),则不等式x+6>-x-2的解集是( A )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
6.如图所示,一次函数y=ax+b(a,b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为x<4.
7.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是.
8.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
解:(1)b=2.
(2)
(3)直线y=nx+m也经过点P.理由:
∵点P(1,2)在直线y=mx+n上,
∴m+n=2,即2=n×1+m.
∴这说明直线y=nx+m也经过点P.
9.如图是直线y=x-5的图象,点P(2,m)在该直线的下方,则m的取值范围是( D )
A.m>-3 B.m>-1 C.m>0 D.m<-3
10.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( D )
A.x<0 B.x>0 C.x<1 D.x>1
11.函数y=2x和y=ax+4的图象相交于点A(m,3),则根据图象可得关于x,y的方程组的解是.
12.已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为x<1.
13.在同一平面直角坐标系内画一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
(1)方程-x+4=2x-5的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
解:如图.(1)由图可知,一次函数y1=-x+4和y2=2x-5的图象相交于点(3,1),
∴方程-x+4=2x-5的解为x=3.
(2)当x<3时,y1>y2;
当x<时,y1>0且y2<0.
14.如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4>kx+b的解集.
解:(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴解得
∴直线AB的解析式为
y=-x+5.
(2)联立解得
∴C(3,2).
(3)根据图象可得x>3.
15.A,B两地相距60 km,甲、乙两人分别从两地出发相向而行,甲先出发.如图,l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是l2(填“l1”或“l2”);甲的速度是30km/h,乙的速度是20km/h;
(2)甲出发多少小时时,两人恰好相距5 km?
解:由图象知,甲离A地
的距离与时间的关系式
是s1=60-30t,乙离A
地的距离与时间的关系
式是s2=20(t-0.5),即
s2=20t-10.
由题意,得60-30t-(20t-10)=5或20t-10-(60-30t)=5,
解得t=1.3或1.5.
答:甲出发1.3 h或1.5 h时,两人恰好相距5 km.
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( )
A.1 B.2 C.3 D.4
2.若方程ax+b=0的解是x=-2,则图中一定不是直线y=ax+b的是( )
A B C D
3.如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4).结合图象可知,关于x的方程ax+b=0的解是 .
4.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
21043906223005.如图所示,直线l1:y=x+6与直线l2:y=-x-2交于点P(-2,3),则不等式x+6>-x-2的解集是( )
A.x>-2
B.x≥-2
C.x<-2
D.x≤-2
6.如图所示,一次函数y=ax+b(a,b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为 .
7.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 .
8.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
9.如图是直线y=x-5的图象,点P(2,m)在该直线的下方,则m的取值范围是( )
286639053340A.m>-3
B.m>-1
C.m>0
D.m<-3
10.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.x<0 B.x>0 C.x<1 D.x>1
11.函数y=2x和y=ax+4的图象相交于点A(m,3),则根据图象可得关于x,y的方程组的解是 .
12.已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为 .
13.在同一平面直角坐标系内画一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
(1)方程-x+4=2x-5的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
14.如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4>kx+b的解集.
15.A,B两地相距60 km,甲、乙两人分别从两地出发相向而行,甲先出发.如图,l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是l2(填“l1”或“l2”);甲的速度是 km/h,乙的速度是 km/h;
(2)甲出发多少小时时,两人恰好相距5 km?
参考答案:
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( A )
A.1 B.2 C.3 D.4
2.若方程ax+b=0的解是x=-2,则图中一定不是直线y=ax+b的是( B )
A B C D
3.如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4).结合图象可知,关于x的方程ax+b=0的解是x=2.
4.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( B )
A.x>2 B.x<2 C.x≥2 D.x≤2
5.如图所示,直线l1:y=x+6与直线l2:y=-x-2交于点P(-2,3),则不等式x+6>-x-2的解集是( A )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
6.如图所示,一次函数y=ax+b(a,b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为x<4.
7.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是.
8.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
解:(1)b=2.
(2)
(3)直线y=nx+m也经过点P.理由:
∵点P(1,2)在直线y=mx+n上,
∴m+n=2,即2=n×1+m.
∴这说明直线y=nx+m也经过点P.
9.如图是直线y=x-5的图象,点P(2,m)在该直线的下方,则m的取值范围是( D )
A.m>-3 B.m>-1 C.m>0 D.m<-3
10.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( D )
A.x<0 B.x>0 C.x<1 D.x>1
11.函数y=2x和y=ax+4的图象相交于点A(m,3),则根据图象可得关于x,y的方程组的解是.
12.已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为x<1.
13.在同一平面直角坐标系内画一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
(1)方程-x+4=2x-5的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
解:如图.(1)由图可知,一次函数y1=-x+4和y2=2x-5的图象相交于点(3,1),
∴方程-x+4=2x-5的解为x=3.
(2)当x<3时,y1>y2;
当x<时,y1>0且y2<0.
14.如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4>kx+b的解集.
解:(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴解得
∴直线AB的解析式为
y=-x+5.
(2)联立解得
∴C(3,2).
(3)根据图象可得x>3.
15.A,B两地相距60 km,甲、乙两人分别从两地出发相向而行,甲先出发.如图,l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是l2(填“l1”或“l2”);甲的速度是30km/h,乙的速度是20km/h;
(2)甲出发多少小时时,两人恰好相距5 km?
解:由图象知,甲离A地
的距离与时间的关系式
是s1=60-30t,乙离A
地的距离与时间的关系
式是s2=20(t-0.5),即
s2=20t-10.
由题意,得60-30t-(20t-10)=5或20t-10-(60-30t)=5,
解得t=1.3或1.5.
答:甲出发1.3 h或1.5 h时,两人恰好相距5 km.
