人教版数学八年级下册:20.1.1 平均数 同步练习试卷(Word版附答案)
文档属性
| 名称 | 人教版数学八年级下册:20.1.1 平均数 同步练习试卷(Word版附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 07:32:35 | ||
图片预览




文档简介
20.1.1 平均数
第1课时 平均数
1.一组数据4,10,12,14,则这组数据的平均数是( )
A.9 B.10 C.11 D.12
2.一组数据2,3,4,x,6的平均数是4,则x是( )
A.2 B.3 C.4 D.5
3.一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
4.10名学生的平均成绩是x,如果另外5名学生每人得90分,那么整个组的平均成绩是( )
A. B. C. D.
5.我市某中学八年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是( )
A.20元 B.15元 C.12元 D.10元
6.某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了两项测试,两人的两项测试成绩如下表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3∶2的比例计算两人的总成绩,那么 (填A或B)将被录用.
7.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
候选人
笔试
口试
得票
甲
85
83
90
乙
80
85
92
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
8.某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为( )
A.7分 B.8分 C.9分 D.10分
9.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种2千克混在一起,则售价应定为每千克( )
A.7元 B.6.7元 C.7.5元 D.8.6元
10.已知x1,x2,x3,x4的平均数是a,则3x1-5,3x2-8,3x3-6,3x4-1的平均数为( )
A.a B.3a C.3a-5 D.3a-8
11.某班50名学生平均身高168 cm,其中30名男生平均身高170 cm,则20名女生的平均身高为 cm.
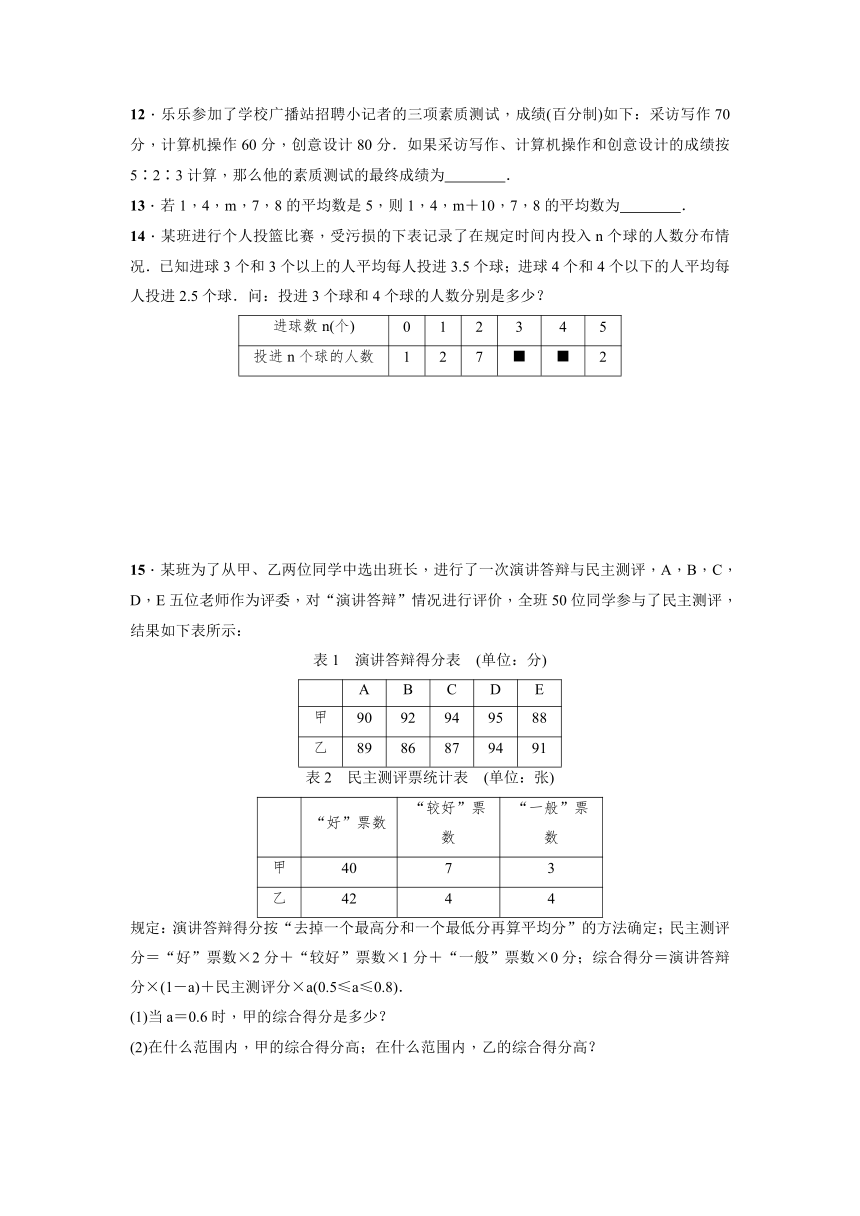
12.乐乐参加了学校广播站招聘小记者的三项素质测试,成绩(百分制)如下:采访写作70分,计算机操作60分,创意设计80分.如果采访写作、计算机操作和创意设计的成绩按5∶2∶3计算,那么他的素质测试的最终成绩为 .
13.若1,4,m,7,8的平均数是5,则1,4,m+10,7,8的平均数为 .
14.某班进行个人投篮比赛,受污损的下表记录了在规定时间内投入n个球的人数分布情况.已知进球3个和3个以上的人平均每人投进3.5个球;进球4个和4个以下的人平均每人投进2.5个球.问:投进3个球和4个球的人数分别是多少?
进球数n(个)
0
1
2
3
4
5
投进n个球的人数
1
2
7
■
■
2
15.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表 (单位:分)
A
B
C
D
E
甲
90
92
94
95
88
乙
89
86
87
94
91
表2 民主测评票统计表 (单位:张)
“好”票数
“较好”票数
“一般”票数
甲
40
7
3
乙
42
4
4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
第2课时 用样本平均数估计总体平均数
1.下列各组数据中,组中值不是10的是( )
A.0≤x<20 B.8≤x<12 C.7≤x<13 D.3≤x<7
2.已知一组数据在5≤x<10的范围内出现了6次,则组中值是 ,权是 .
3.对一组数据进行整理,结果如下表,这组数据的平均数是 .
分组
频数
0≤x<10
12
10≤x<20
20
4.某“中学生暑期环保小组”的同学随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):7,5,7,8,7,5,8,9,5,9.根据提供的数据,该小区2 000户家庭一周内需要环保方便袋约( )
A.2 000只 B.14 000只 C.21 000只 D.98 000只
5.某地区有一条长100千米、宽0.5千米的防护林.有关部门为统计该防护林的树木量,从中选出5块防护林(每块长1千米,宽0.5千米)进行统计,每块防护林的树木数量如下(单位:棵):65 100,63 200,64 600,64 700,67 400.那么根据以上的数据估算这一防护林总共约有 棵树.
6.某外贸公司要出口一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:
-10,+5,0,+5,0,0,-5,0,+5,+10.
则可估计这批食品罐头质量的平均数约为( )
A.453克 B.454克 C.455克 D.456克
7.某部队为测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(米)如下表:
杀伤半径
20≤x<40
40≤x<60
60≤x<80
80≤x<100
数量
8
12
25
5
则这批炮弹的平均杀伤半径是 米.
8.随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2 200
1 780
7 560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
9.为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.
回答下列问题:
(1)这次被抽查的学生共有 人,扇形统计图中,“B组”所对应的圆心角的度数为 .
(2)补全条形统计图.
(3)已知该中学共有学生2 500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?
参考答案:
20.1.1 平均数
第1课时 平均数
1.一组数据4,10,12,14,则这组数据的平均数是( B )
A.9 B.10 C.11 D.12
2.一组数据2,3,4,x,6的平均数是4,则x是( D )
A.2 B.3 C.4 D.5
3.一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
解:该同学这五次投实心球的平均成绩为
=10.4(m).
4.10名学生的平均成绩是x,如果另外5名学生每人得90分,那么整个组的平均成绩是( D )
A. B. C. D.
5.我市某中学八年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是( D )
A.20元 B.15元 C.12元 D.10元
6.某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了两项测试,两人的两项测试成绩如下表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3∶2的比例计算两人的总成绩,那么B(填A或B)将被录用.
7.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
候选人
笔试
口试
得票
甲
85
83
90
乙
80
85
92
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
解:(1)甲的成绩为:85×20%+83×30%+90×50%=86.9(分),
乙的成绩为:80×20%+85×30%+92×50%=87.5(分),
因此,乙会竞选上.
(2)甲的成绩为:=86.6(分),
乙的成绩为:=85.8(分),
因此,甲会竞选上.
8.某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为( B )
A.7分 B.8分 C.9分 D.10分
9.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种2千克混在一起,则售价应定为每千克( B )
A.7元 B.6.7元 C.7.5元 D.8.6元
10.已知x1,x2,x3,x4的平均数是a,则3x1-5,3x2-8,3x3-6,3x4-1的平均数为( C )
A.a B.3a C.3a-5 D.3a-8
11.某班50名学生平均身高168 cm,其中30名男生平均身高170 cm,则20名女生的平均身高为165cm.
12.乐乐参加了学校广播站招聘小记者的三项素质测试,成绩(百分制)如下:采访写作70分,计算机操作60分,创意设计80分.如果采访写作、计算机操作和创意设计的成绩按5∶2∶3计算,那么他的素质测试的最终成绩为71分.
13.若1,4,m,7,8的平均数是5,则1,4,m+10,7,8的平均数为7.
14.某班进行个人投篮比赛,受污损的下表记录了在规定时间内投入n个球的人数分布情况.已知进球3个和3个以上的人平均每人投进3.5个球;进球4个和4个以下的人平均每人投进2.5个球.问:投进3个球和4个球的人数分别是多少?
进球数n(个)
0
1
2
3
4
5
投进n个球的人数
1
2
7
■
■
2
解:设投进3个球的有x人,投进4个球的有y人.根据题意,得
解得
经检验,是原方程组的解,且符合题意.
答:投进3个球的有9人,投进4个球的有3人.
15.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表 (单位:分)
A
B
C
D
E
甲
90
92
94
95
88
乙
89
86
87
94
91
表2 民主测评票统计表 (单位:张)
“好”票数
“较好”票数
“一般”票数
甲
40
7
3
乙
42
4
4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
解:(1)甲的演讲答辩得分==92(分),
甲的民主测评得分=40×2+7×1+3×0=87(分),
当a=0.6时,甲的综合得分=92×(1-0.6)+87×0.6=36.8+52.2=89(分).
(2)∵乙的演讲答辩得分==89(分),
乙的民主测评得分=42×2+4×1+4×0=88(分),
∴乙的综合得分=89(1-a)+88a.
由(1)知甲的综合得分=92(1-a)+87a.
当92(1-a)+87a>89(1-a)+88a时,
即有a<0.75.
又∵0.5≤a≤0.8,
∴当0.5≤a<0.75时,甲的综合得分高.
当92(1-a)+87a<89(1-a)+88a时,
即有a>0.75.
又∵0.5≤a≤0.8,
∴当0.75<a≤0.8时,乙的综合得分高.
第2课时 用样本平均数估计总体平均数
1.下列各组数据中,组中值不是10的是( D )
A.0≤x<20 B.8≤x<12 C.7≤x<13 D.3≤x<7
2.已知一组数据在5≤x<10的范围内出现了6次,则组中值是7.5,权是6.
3.对一组数据进行整理,结果如下表,这组数据的平均数是11.25.
分组
频数
0≤x<10
12
10≤x<20
20
4.某“中学生暑期环保小组”的同学随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):7,5,7,8,7,5,8,9,5,9.根据提供的数据,该小区2 000户家庭一周内需要环保方便袋约( B )
A.2 000只 B.14 000只 C.21 000只 D.98 000只
5.某地区有一条长100千米、宽0.5千米的防护林.有关部门为统计该防护林的树木量,从中选出5块防护林(每块长1千米,宽0.5千米)进行统计,每块防护林的树木数量如下(单位:棵):65 100,63 200,64 600,64 700,67 400.那么根据以上的数据估算这一防护林总共约有6_500_000棵树.
6.某外贸公司要出口一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:
-10,+5,0,+5,0,0,-5,0,+5,+10.
则可估计这批食品罐头质量的平均数约为( C )
A.453克 B.454克 C.455克 D.456克
7.某部队为测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(米)如下表:
杀伤半径
20≤x<40
40≤x<60
60≤x<80
80≤x<100
数量
8
12
25
5
则这批炮弹的平均杀伤半径是60.8米.
8.随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2 200
1 780
7 560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
解:(1)该店本周的日平均营业额为7 560÷7=1 080(元).
(2)因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额,
所以去掉周六、日的营业额对平均数的影响较大,
故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合理.
方案:用该店本周一到周日的日平均营业额估计当月营业总额,
当月的营业额为30×1 080=32 400(元).
9.为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.
回答下列问题:
(1)这次被抽查的学生共有120人,扇形统计图中,“B组”所对应的圆心角的度数为72°.
(2)补全条形统计图.
(3)已知该中学共有学生2 500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?
解:(2)补全条形统计图如图.
(3)这日午饭有剩饭的学生人数为:
2 500×(1-60%-10%)=750(人),
750×10=7 500(克)=7.5(千克).
答:这日午饭将浪费7.5千克米饭.
第1课时 平均数
1.一组数据4,10,12,14,则这组数据的平均数是( )
A.9 B.10 C.11 D.12
2.一组数据2,3,4,x,6的平均数是4,则x是( )
A.2 B.3 C.4 D.5
3.一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
4.10名学生的平均成绩是x,如果另外5名学生每人得90分,那么整个组的平均成绩是( )
A. B. C. D.
5.我市某中学八年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是( )
A.20元 B.15元 C.12元 D.10元
6.某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了两项测试,两人的两项测试成绩如下表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3∶2的比例计算两人的总成绩,那么 (填A或B)将被录用.
7.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
候选人
笔试
口试
得票
甲
85
83
90
乙
80
85
92
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
8.某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为( )
A.7分 B.8分 C.9分 D.10分
9.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种2千克混在一起,则售价应定为每千克( )
A.7元 B.6.7元 C.7.5元 D.8.6元
10.已知x1,x2,x3,x4的平均数是a,则3x1-5,3x2-8,3x3-6,3x4-1的平均数为( )
A.a B.3a C.3a-5 D.3a-8
11.某班50名学生平均身高168 cm,其中30名男生平均身高170 cm,则20名女生的平均身高为 cm.
12.乐乐参加了学校广播站招聘小记者的三项素质测试,成绩(百分制)如下:采访写作70分,计算机操作60分,创意设计80分.如果采访写作、计算机操作和创意设计的成绩按5∶2∶3计算,那么他的素质测试的最终成绩为 .
13.若1,4,m,7,8的平均数是5,则1,4,m+10,7,8的平均数为 .
14.某班进行个人投篮比赛,受污损的下表记录了在规定时间内投入n个球的人数分布情况.已知进球3个和3个以上的人平均每人投进3.5个球;进球4个和4个以下的人平均每人投进2.5个球.问:投进3个球和4个球的人数分别是多少?
进球数n(个)
0
1
2
3
4
5
投进n个球的人数
1
2
7
■
■
2
15.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表 (单位:分)
A
B
C
D
E
甲
90
92
94
95
88
乙
89
86
87
94
91
表2 民主测评票统计表 (单位:张)
“好”票数
“较好”票数
“一般”票数
甲
40
7
3
乙
42
4
4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
第2课时 用样本平均数估计总体平均数
1.下列各组数据中,组中值不是10的是( )
A.0≤x<20 B.8≤x<12 C.7≤x<13 D.3≤x<7
2.已知一组数据在5≤x<10的范围内出现了6次,则组中值是 ,权是 .
3.对一组数据进行整理,结果如下表,这组数据的平均数是 .
分组
频数
0≤x<10
12
10≤x<20
20
4.某“中学生暑期环保小组”的同学随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):7,5,7,8,7,5,8,9,5,9.根据提供的数据,该小区2 000户家庭一周内需要环保方便袋约( )
A.2 000只 B.14 000只 C.21 000只 D.98 000只
5.某地区有一条长100千米、宽0.5千米的防护林.有关部门为统计该防护林的树木量,从中选出5块防护林(每块长1千米,宽0.5千米)进行统计,每块防护林的树木数量如下(单位:棵):65 100,63 200,64 600,64 700,67 400.那么根据以上的数据估算这一防护林总共约有 棵树.
6.某外贸公司要出口一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:
-10,+5,0,+5,0,0,-5,0,+5,+10.
则可估计这批食品罐头质量的平均数约为( )
A.453克 B.454克 C.455克 D.456克
7.某部队为测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(米)如下表:
杀伤半径
20≤x<40
40≤x<60
60≤x<80
80≤x<100
数量
8
12
25
5
则这批炮弹的平均杀伤半径是 米.
8.随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2 200
1 780
7 560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
9.为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.
回答下列问题:
(1)这次被抽查的学生共有 人,扇形统计图中,“B组”所对应的圆心角的度数为 .
(2)补全条形统计图.
(3)已知该中学共有学生2 500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?
参考答案:
20.1.1 平均数
第1课时 平均数
1.一组数据4,10,12,14,则这组数据的平均数是( B )
A.9 B.10 C.11 D.12
2.一组数据2,3,4,x,6的平均数是4,则x是( D )
A.2 B.3 C.4 D.5
3.一位同学进行五次投实心球的练习,每次投出的成绩如表:
投实心球序次
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
解:该同学这五次投实心球的平均成绩为
=10.4(m).
4.10名学生的平均成绩是x,如果另外5名学生每人得90分,那么整个组的平均成绩是( D )
A. B. C. D.
5.我市某中学八年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是( D )
A.20元 B.15元 C.12元 D.10元
6.某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了两项测试,两人的两项测试成绩如下表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3∶2的比例计算两人的总成绩,那么B(填A或B)将被录用.
7.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
候选人
笔试
口试
得票
甲
85
83
90
乙
80
85
92
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
解:(1)甲的成绩为:85×20%+83×30%+90×50%=86.9(分),
乙的成绩为:80×20%+85×30%+92×50%=87.5(分),
因此,乙会竞选上.
(2)甲的成绩为:=86.6(分),
乙的成绩为:=85.8(分),
因此,甲会竞选上.
8.某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为( B )
A.7分 B.8分 C.9分 D.10分
9.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种2千克混在一起,则售价应定为每千克( B )
A.7元 B.6.7元 C.7.5元 D.8.6元
10.已知x1,x2,x3,x4的平均数是a,则3x1-5,3x2-8,3x3-6,3x4-1的平均数为( C )
A.a B.3a C.3a-5 D.3a-8
11.某班50名学生平均身高168 cm,其中30名男生平均身高170 cm,则20名女生的平均身高为165cm.
12.乐乐参加了学校广播站招聘小记者的三项素质测试,成绩(百分制)如下:采访写作70分,计算机操作60分,创意设计80分.如果采访写作、计算机操作和创意设计的成绩按5∶2∶3计算,那么他的素质测试的最终成绩为71分.
13.若1,4,m,7,8的平均数是5,则1,4,m+10,7,8的平均数为7.
14.某班进行个人投篮比赛,受污损的下表记录了在规定时间内投入n个球的人数分布情况.已知进球3个和3个以上的人平均每人投进3.5个球;进球4个和4个以下的人平均每人投进2.5个球.问:投进3个球和4个球的人数分别是多少?
进球数n(个)
0
1
2
3
4
5
投进n个球的人数
1
2
7
■
■
2
解:设投进3个球的有x人,投进4个球的有y人.根据题意,得
解得
经检验,是原方程组的解,且符合题意.
答:投进3个球的有9人,投进4个球的有3人.
15.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表 (单位:分)
A
B
C
D
E
甲
90
92
94
95
88
乙
89
86
87
94
91
表2 民主测评票统计表 (单位:张)
“好”票数
“较好”票数
“一般”票数
甲
40
7
3
乙
42
4
4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
解:(1)甲的演讲答辩得分==92(分),
甲的民主测评得分=40×2+7×1+3×0=87(分),
当a=0.6时,甲的综合得分=92×(1-0.6)+87×0.6=36.8+52.2=89(分).
(2)∵乙的演讲答辩得分==89(分),
乙的民主测评得分=42×2+4×1+4×0=88(分),
∴乙的综合得分=89(1-a)+88a.
由(1)知甲的综合得分=92(1-a)+87a.
当92(1-a)+87a>89(1-a)+88a时,
即有a<0.75.
又∵0.5≤a≤0.8,
∴当0.5≤a<0.75时,甲的综合得分高.
当92(1-a)+87a<89(1-a)+88a时,
即有a>0.75.
又∵0.5≤a≤0.8,
∴当0.75<a≤0.8时,乙的综合得分高.
第2课时 用样本平均数估计总体平均数
1.下列各组数据中,组中值不是10的是( D )
A.0≤x<20 B.8≤x<12 C.7≤x<13 D.3≤x<7
2.已知一组数据在5≤x<10的范围内出现了6次,则组中值是7.5,权是6.
3.对一组数据进行整理,结果如下表,这组数据的平均数是11.25.
分组
频数
0≤x<10
12
10≤x<20
20
4.某“中学生暑期环保小组”的同学随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):7,5,7,8,7,5,8,9,5,9.根据提供的数据,该小区2 000户家庭一周内需要环保方便袋约( B )
A.2 000只 B.14 000只 C.21 000只 D.98 000只
5.某地区有一条长100千米、宽0.5千米的防护林.有关部门为统计该防护林的树木量,从中选出5块防护林(每块长1千米,宽0.5千米)进行统计,每块防护林的树木数量如下(单位:棵):65 100,63 200,64 600,64 700,67 400.那么根据以上的数据估算这一防护林总共约有6_500_000棵树.
6.某外贸公司要出口一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:
-10,+5,0,+5,0,0,-5,0,+5,+10.
则可估计这批食品罐头质量的平均数约为( C )
A.453克 B.454克 C.455克 D.456克
7.某部队为测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(米)如下表:
杀伤半径
20≤x<40
40≤x<60
60≤x<80
80≤x<100
数量
8
12
25
5
则这批炮弹的平均杀伤半径是60.8米.
8.随机抽取某理发店一周的营业额如下表(单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
540
680
760
640
960
2 200
1 780
7 560
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
解:(1)该店本周的日平均营业额为7 560÷7=1 080(元).
(2)因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额,
所以去掉周六、日的营业额对平均数的影响较大,
故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合理.
方案:用该店本周一到周日的日平均营业额估计当月营业总额,
当月的营业额为30×1 080=32 400(元).
9.为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.
回答下列问题:
(1)这次被抽查的学生共有120人,扇形统计图中,“B组”所对应的圆心角的度数为72°.
(2)补全条形统计图.
(3)已知该中学共有学生2 500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?
解:(2)补全条形统计图如图.
(3)这日午饭有剩饭的学生人数为:
2 500×(1-60%-10%)=750(人),
750×10=7 500(克)=7.5(千克).
答:这日午饭将浪费7.5千克米饭.
