3.2 用关系式表示的变量间的关系课件(共19张PPT)
文档属性
| 名称 | 3.2 用关系式表示的变量间的关系课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 05:57:12 | ||
图片预览





文档简介
3.2用关系式表示的变量间的关系
第三章
变量之间的关系
2021年春北师大版七年级数学下册
学习目标
1.能根据具体情况,用关系式表示某些变量之间的关系;
2.能根据关系式求值,进一步体会自变量和因变量的数值对应关系。
导入新课
在“小车下滑的时间”中,
1.支撑物的高度h和小车下滑的时间t都在变化,它们都是变量.其中小车下滑的时间t随支撑物的高度h的变化而变化,
2.支撑物的高度h是自变量,
3.小车下滑的时间t是因变量.
确定一个三角形面积的量有哪些?
D
B
C
A
三角形的底和高
用关系式表示变量间的关系
探究新知
如图,三角形ABC底边BC上的高是6厘米.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中,自变量和因变量分别是
什么?
三角形的底边长度是自变量,
三角形的面积是因变量.
探究新知
(2)如果三角形的底边长为x(厘米),那么三
角形的面积y(厘米2)可以表示为________.
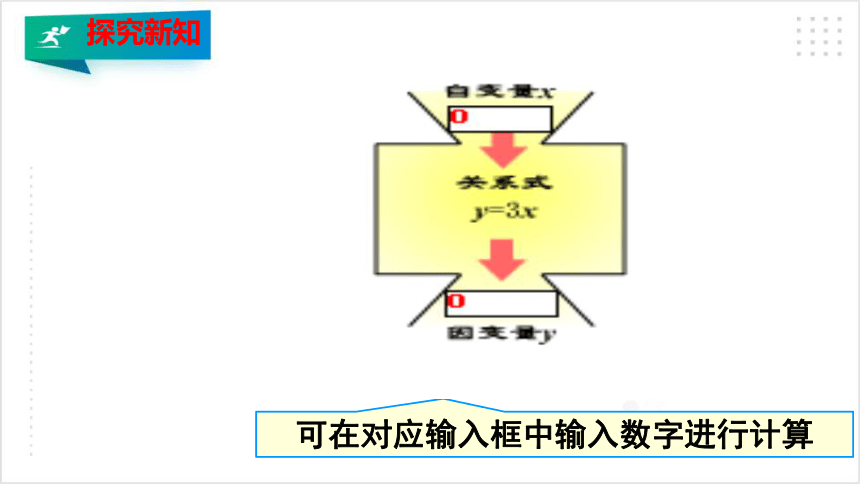
y=3x
(3)当底边长从12厘米变化到3厘米时,三角形
的面积从_____厘米2变化到_____厘米2.
36
9
探究新知
可在对应输入框中输入数字进行计算
探究新知
归纳总结
y=3x表示了三角形面积和三角形底边长之间的关系,它是变量y随x变化的关系式.
注意:关系式是我们表示变量
之间关系的另一种方法,
利用关系式,如y=3x,
我们可以根据任何一个
自变量值求出相应的因
变量的值.
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
r
h
思考
探究新知
变化中的圆锥
h
r
r
h
底面半径不变
高变
高不变
底面半径变
探究新知
AD由小变大时,三角形的面积发生了变化。
(1)在这个变化过程中,____________是自
变量,______________是因变量。
(2)若三角形的高为h cm,面积为S cm2。
则S与h的关系式是_______。
(3)当高从2cm变到10cm时,三角形的
面积由______变化为______。
(4)当面积为40cm2时,高为_____cm。
A
C
B
D
如图,△ABC中,边BC=4cm,当△ABC的高
三角形的高
S=2h
三角形的面积
4cm2
20cm2
20
探究新知
1.变量x与y之间的关系式是y=x2-3,当自变量x=2
时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
C
【解析】将x=2代入y=x2-3,得y=22-3=1.
课堂练习
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
【解析】由题意,有y=2(5-x),即y=10-2x.
B
课堂练习
3.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各
是什么?
(2)写出圆柱的体积V与高h之间的关系式.
自变量是圆柱的高,因变量是圆柱的体积.
V= =πh.
课堂练习
3.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
当h=10cm时,V=πh=10πcm3;
当h=5cm时,V=πh=5πcm3.
所以当h由10cm变化到5cm时,
V从10πcm3变化到5πcm3.
V=0,此时表示平面图形——直径为2cm的圆.
课堂练习
高度d/m
0
200
400
600
800
1000
温度T/oC
7.33
8.67
6.00
4.67
3.33
10.00
4.在地球某地,温度T(℃)与高度d(m)的关系可以近似地用 来表示。根据这个关系式,当d的值分别是0,200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果。
解:
自变量
因变量
课堂练习
课堂小结
2、列表与列关系式表示变量之间的关系各有
什么特点?
1、到今天为止我们一共学了几种方法来表示
自变量与因变量之间的关系?
列表格与列关系式两种方法
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况。
利用关系式,我们可以根据一个自变量的值求出相应的因变量的值。
https://www.21cnjy.com/help/help_extract.php
第三章
变量之间的关系
2021年春北师大版七年级数学下册
学习目标
1.能根据具体情况,用关系式表示某些变量之间的关系;
2.能根据关系式求值,进一步体会自变量和因变量的数值对应关系。
导入新课
在“小车下滑的时间”中,
1.支撑物的高度h和小车下滑的时间t都在变化,它们都是变量.其中小车下滑的时间t随支撑物的高度h的变化而变化,
2.支撑物的高度h是自变量,
3.小车下滑的时间t是因变量.
确定一个三角形面积的量有哪些?
D
B
C
A
三角形的底和高
用关系式表示变量间的关系
探究新知
如图,三角形ABC底边BC上的高是6厘米.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中,自变量和因变量分别是
什么?
三角形的底边长度是自变量,
三角形的面积是因变量.
探究新知
(2)如果三角形的底边长为x(厘米),那么三
角形的面积y(厘米2)可以表示为________.
y=3x
(3)当底边长从12厘米变化到3厘米时,三角形
的面积从_____厘米2变化到_____厘米2.
36
9
探究新知
可在对应输入框中输入数字进行计算
探究新知
归纳总结
y=3x表示了三角形面积和三角形底边长之间的关系,它是变量y随x变化的关系式.
注意:关系式是我们表示变量
之间关系的另一种方法,
利用关系式,如y=3x,
我们可以根据任何一个
自变量值求出相应的因
变量的值.
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
r
h
思考
探究新知
变化中的圆锥
h
r
r
h
底面半径不变
高变
高不变
底面半径变
探究新知
AD由小变大时,三角形的面积发生了变化。
(1)在这个变化过程中,____________是自
变量,______________是因变量。
(2)若三角形的高为h cm,面积为S cm2。
则S与h的关系式是_______。
(3)当高从2cm变到10cm时,三角形的
面积由______变化为______。
(4)当面积为40cm2时,高为_____cm。
A
C
B
D
如图,△ABC中,边BC=4cm,当△ABC的高
三角形的高
S=2h
三角形的面积
4cm2
20cm2
20
探究新知
1.变量x与y之间的关系式是y=x2-3,当自变量x=2
时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
C
【解析】将x=2代入y=x2-3,得y=22-3=1.
课堂练习
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
【解析】由题意,有y=2(5-x),即y=10-2x.
B
课堂练习
3.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各
是什么?
(2)写出圆柱的体积V与高h之间的关系式.
自变量是圆柱的高,因变量是圆柱的体积.
V= =πh.
课堂练习
3.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
当h=10cm时,V=πh=10πcm3;
当h=5cm时,V=πh=5πcm3.
所以当h由10cm变化到5cm时,
V从10πcm3变化到5πcm3.
V=0,此时表示平面图形——直径为2cm的圆.
课堂练习
高度d/m
0
200
400
600
800
1000
温度T/oC
7.33
8.67
6.00
4.67
3.33
10.00
4.在地球某地,温度T(℃)与高度d(m)的关系可以近似地用 来表示。根据这个关系式,当d的值分别是0,200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果。
解:
自变量
因变量
课堂练习
课堂小结
2、列表与列关系式表示变量之间的关系各有
什么特点?
1、到今天为止我们一共学了几种方法来表示
自变量与因变量之间的关系?
列表格与列关系式两种方法
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况。
利用关系式,我们可以根据一个自变量的值求出相应的因变量的值。
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
