7.1.2 复数的几何意义(课件(共20张PPT))-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册
文档属性
| 名称 | 7.1.2 复数的几何意义(课件(共20张PPT))-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第7章
复数
7.1.2
复数的几何意义
实数可以用数轴上的点来表示.
实数
数轴上的点
(形)
(数)
一一对应
创设情境
回顾初中在几何上,我们用什么来表示实数?
思考
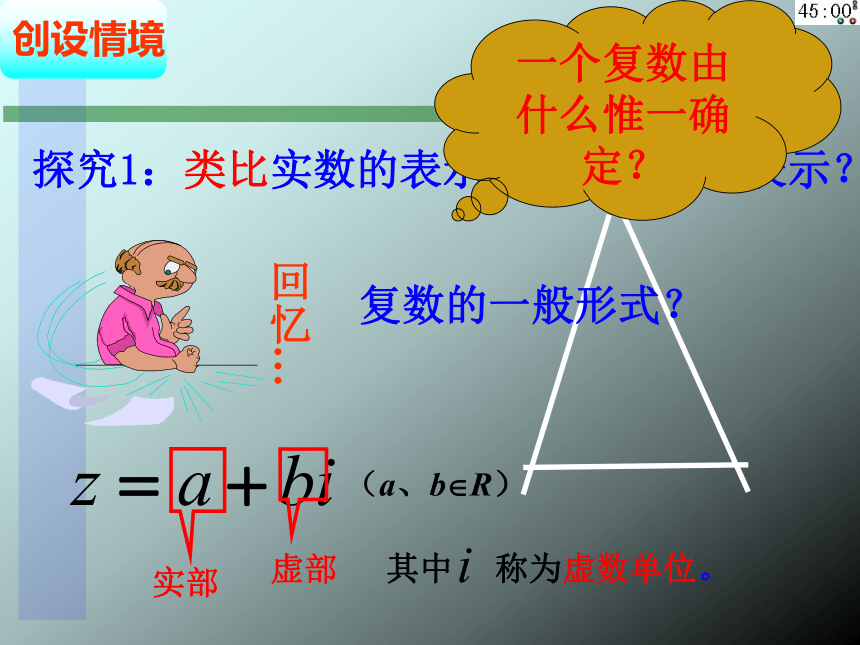
探究1:类比实数的表示,复数如何来表示?
创设情境
回忆…
一个复数由什么惟一确定?
复数的一般形式?
实部
虚部
其中
称为虚数单位。
(a、b?R)
复数z=a+bi
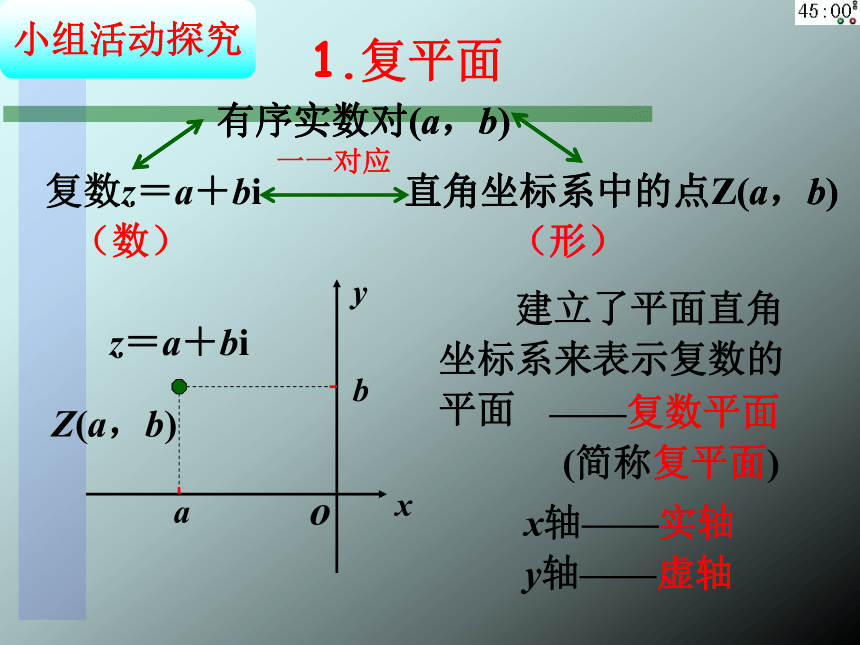
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x
y
o
b
a
Z(a,b)
建立了平面直角坐标系来表示复数的平面
x轴——实轴
y轴——虚轴
(数)
(形)
——复数平面
(简称复平面)
一一对应
z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(形)
小组活动探究
1.复平面
探究2:
建构数学
实轴、虚轴上的点与复数的对应关系
返
回
建构数学
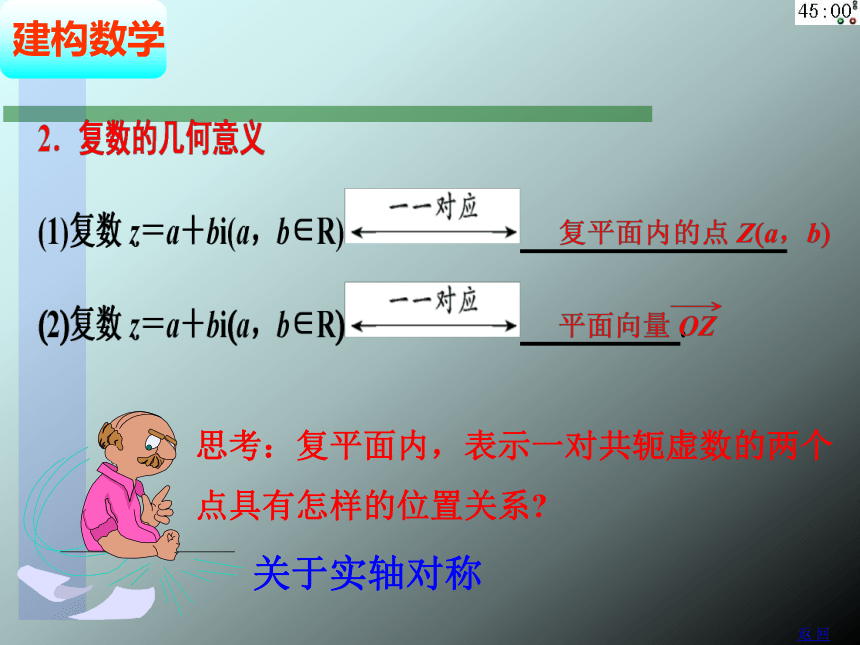
思考:复平面内,表示一对共轭虚数的两个点具有怎样的位置关系?
关于实轴对称
建构数学
试一试
1.如果复平面内表示两个虚数的点关于原点对称,那么它们的实部和虚部分别满足什么关系?
2.“a=0”是“复数a+bi
(a,b∈R)所对应的点在虚轴上”的____________条件.
互为相反数
充要条件
例1.已知复数z=(m2+m-6)
+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围.
数学应用
数学应用
数学应用
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
数学应用
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
平面向量
一一对应
一一对应
x
y
o
b
a
Z(a,b)
z=a+bi
小结
小组活动探究
小组活动探究
实数绝对值的几何意义是什么?
能否类比定义复数的绝对值?
对应平面向量
的模|
|,即复数z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
建构数学
数学应用
求|z1|及|z2|的值;
试比较它们模的大小.
|z1|>|z2|
数学应用
例3.
设z∈C
,满足下列条件的点Z的集合是什么图形?
(1)│Z│=2,
(2)2<│Z│<3.
数学应用
重要数学思想:
数形结合
回顾小结
重要知识:
(1)复平面、实轴、虚轴、模的概念.
(2)复数与点、向量间的对应关系.
(3)复数加法、减法的几何意义及其应用.
注意:利用复数的几何意义求参数的值或范围出错.
课后练习
当
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
∴复数z=(3m-2)+(m-1)i在复平面内对应的点位
于第四象限.
数学世界是个有趣的世界,希望同学们从数学问题的解决中感受到她的乐趣和魅力!
结束寄语
第7章
复数
7.1.2
复数的几何意义
实数可以用数轴上的点来表示.
实数
数轴上的点
(形)
(数)
一一对应
创设情境
回顾初中在几何上,我们用什么来表示实数?
思考
探究1:类比实数的表示,复数如何来表示?
创设情境
回忆…
一个复数由什么惟一确定?
复数的一般形式?
实部
虚部
其中
称为虚数单位。
(a、b?R)
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x
y
o
b
a
Z(a,b)
建立了平面直角坐标系来表示复数的平面
x轴——实轴
y轴——虚轴
(数)
(形)
——复数平面
(简称复平面)
一一对应
z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(形)
小组活动探究
1.复平面
探究2:
建构数学
实轴、虚轴上的点与复数的对应关系
返
回
建构数学
思考:复平面内,表示一对共轭虚数的两个点具有怎样的位置关系?
关于实轴对称
建构数学
试一试
1.如果复平面内表示两个虚数的点关于原点对称,那么它们的实部和虚部分别满足什么关系?
2.“a=0”是“复数a+bi
(a,b∈R)所对应的点在虚轴上”的____________条件.
互为相反数
充要条件
例1.已知复数z=(m2+m-6)
+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围.
数学应用
数学应用
数学应用
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
数学应用
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
平面向量
一一对应
一一对应
x
y
o
b
a
Z(a,b)
z=a+bi
小结
小组活动探究
小组活动探究
实数绝对值的几何意义是什么?
能否类比定义复数的绝对值?
对应平面向量
的模|
|,即复数z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
建构数学
数学应用
求|z1|及|z2|的值;
试比较它们模的大小.
|z1|>|z2|
数学应用
例3.
设z∈C
,满足下列条件的点Z的集合是什么图形?
(1)│Z│=2,
(2)2<│Z│<3.
数学应用
重要数学思想:
数形结合
回顾小结
重要知识:
(1)复平面、实轴、虚轴、模的概念.
(2)复数与点、向量间的对应关系.
(3)复数加法、减法的几何意义及其应用.
注意:利用复数的几何意义求参数的值或范围出错.
课后练习
当
A.第一象限
B.第二象限
C.第三象限
D.第四象限
∴复数z=(3m-2)+(m-1)i在复平面内对应的点位
于第四象限.
数学世界是个有趣的世界,希望同学们从数学问题的解决中感受到她的乐趣和魅力!
结束寄语
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
