2020-2021学年浙江省名校协作体高二(下)开学数学试卷(Word解析版)
文档属性
| 名称 | 2020-2021学年浙江省名校协作体高二(下)开学数学试卷(Word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 10:58:05 | ||
图片预览



文档简介
2020-2021学年浙江省名校协作体高二(下)开学数学试卷
一、选择题(共10小题).
1.直线x+y﹣1=0的倾斜角为( )
A.30° B.60° C.120° D.150°
2.直线2x+3y=0是双曲线的一条渐近线,则实数a的值为( )
A. B.3 C. D.
3.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
A.若m∥n,n?α,则m∥α B.若m∥α,m∥β,则α∥β
C.若m⊥α,n⊥α,则m∥n D.若α⊥γ,β⊥γ,则α∥β
4.“m=﹣1”是“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.在四面体O﹣ABC中,点P为棱BC的中点.设,,,那么向量用基底{,,}可表示为( )
A. B.
C. D.
6.已知平面α和两条异面直线a,b满足a?α,b⊥α,平面α内的动点M到两条直线a,b的距离相等,则点M的轨迹是( )
A.两条直线 B.椭圆 C.双曲线 D.抛物线
7.圆x2+y2﹣mx+y+m=0在x轴上截得的弦长是它在y轴上截得的弦长的2倍,则实数m的值是( )
A. B. C. D.
8.正三棱锥A﹣BCD中,二面角A﹣BC﹣D的大小为α,二面角B﹣AC﹣D的大小为β,则cos2α+cosβ的取值范围是( )
A. B. C. D.
9.曲线C1:y2=6|x|与C2:=1交点的个数为( )
A.1 B.2 C.3 D.4
10.在正四面体ABCD中,P,Q分别是棱AB,CD的中点,E,F分别是直线AB,CD上的动点,且满足|PE|+|QF|=a,M是EF的中点,则点M的轨迹围成的区域的面积是( )
A. B. C. D.
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
11.已知抛物线C的焦点F(1,0),则拋物线C的标准方程为 ,焦点到准线的距离为 .
12.已知某几何体的三视图如图,则该几何体的体积为 cm3,表面积为 cm2.
13.若直线l1:y=kx+1与直线l2关于点(2,3)对称,则直线l2恒过定点 ,l1与l2的距离的最大值是 .
14.已知P是圆C:(x﹣3)2+(y﹣4)2=1上一动点,过圆心C作两条互相垂直的直线l1,l2,它们分别交x轴于A点,交y轴于B点,记AB中点为Q,则PQ的最小值是 ,圆C上到Q的距离等于3的点有 个.
15.已知平面α∥β,直线l与α所成角的正切值为,直线m?α,l⊥m,直线n?β,且l和n所成角为,那么m与n所成的角为 .
16.已知椭圆C:=1,过C上一点P(第一象限)的直线l与x轴正半轴,y轴正半轴分别交于点A,B.若|PA|=1,则|PB|的值为 .
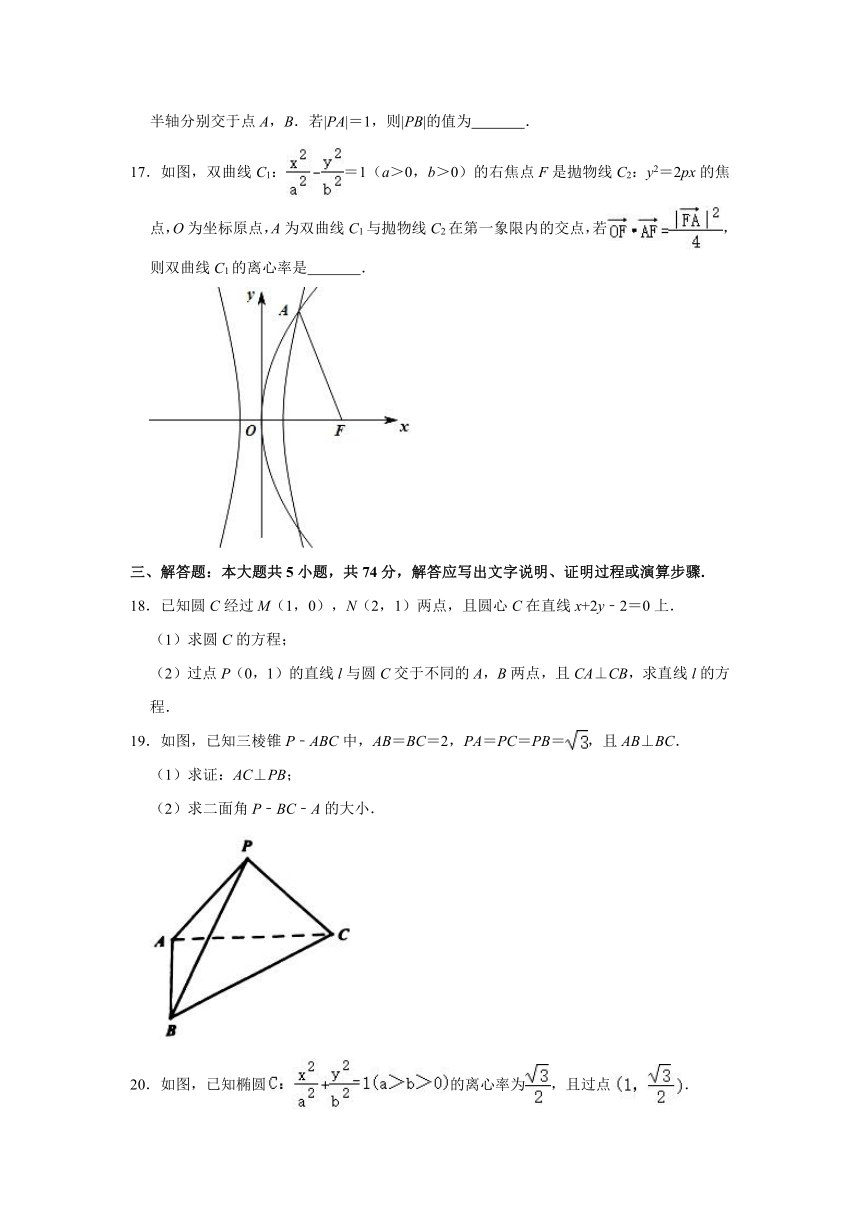
17.如图,双曲线C1:=1(a>0,b>0)的右焦点F是拋物线C2:y2=2px的焦点,O为坐标原点,A为双曲线C1与拋物线C2在第一象限内的交点,若,则双曲线C1的离心率是 .
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.已知圆C经过M(1,0),N(2,1)两点,且圆心C在直线x+2y﹣2=0上.
(1)求圆C的方程;
(2)过点P(0,1)的直线l与圆C交于不同的A,B两点,且CA⊥CB,求直线l的方程.
19.如图,已知三棱锥P﹣ABC中,AB=BC=2,PA=PC=PB=,且AB⊥BC.
(1)求证:AC⊥PB;
(2)求二面角P﹣BC﹣A的大小.
20.如图,已知椭圆的离心率为,且过点.
(1)求椭圆C的标准方程;
(2)过左焦点F且斜率为正的直线l与椭圆C交于A、B两点,过点A、B分别作与直线l垂直的直线,交x轴于C、D两点,求|FC|?|FD|的最小值.
21.在三棱台ABC﹣DEF中,AB=BC=2DE,∠DAB=∠EBA=60°,平面ABED⊥平面ABC,BC⊥BE.
(1)求证:平面ABED⊥平面BCFE;
(2)求直线DF与平面ABF所成角的正弦值.
22.如图,已知过拋物线C:y2=4x的焦点F的直线交抛物线C于点A,B(点A在第一象限),线段AB的中点为M,拋物线C在点A处的切线与以AM为直径的圆交于另一点P.
(1)若,求直线AB的方程;
(2)试问是否为定值?若是,请求出该定值;若不是,请求出它的最大值.
参考答案
一、选择题(共10小题).
1.直线x+y﹣1=0的倾斜角为( )
A.30° B.60° C.120° D.150°
解:设直线x+y﹣1=0的倾斜角为α.
直线x+y﹣1=0化为.
∴tanα=﹣.
∵α∈[0°,180°),
∴α=150°.
故选:D.
2.直线2x+3y=0是双曲线的一条渐近线,则实数a的值为( )
A. B.3 C. D.
解:双曲线的渐近线方程为,化为2x±ay=0,
又2x+3y=0是双曲线的一条渐近线,∴a=3.
故选:B.
3.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
A.若m∥n,n?α,则m∥α B.若m∥α,m∥β,则α∥β
C.若m⊥α,n⊥α,则m∥n D.若α⊥γ,β⊥γ,则α∥β
解:若m∥n,n?α,且m?α,则m∥α,故A错误;
若m∥α,m∥β,则α∥β,或α、β相交,故B错误;
若m⊥α,n⊥α,则m∥n,故C正确;
若α⊥γ,β⊥γ,则α∥β,或α、β相交,故D错误.
故选:C.
4.“m=﹣1”是“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”?2m+m(m﹣1)=0,解得m=0,或m=﹣1.
∴“m=﹣1”是“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”的充分不必要条件.
故选:A.
5.在四面体O﹣ABC中,点P为棱BC的中点.设,,,那么向量用基底{,,}可表示为( )
A. B.
C. D.
解:∵点P为棱BC的中点,
∴=(+),
∴==(+)﹣,
又∵,,,
∴=(+)﹣=﹣++.
故选:B.
6.已知平面α和两条异面直线a,b满足a?α,b⊥α,平面α内的动点M到两条直线a,b的距离相等,则点M的轨迹是( )
A.两条直线 B.椭圆 C.双曲线 D.抛物线
解:b⊥α,设垂足为B,则M到直线b的距离即为M到定点B的距离,
即动点M在平面α内到一定直线距离与一定点的距离相等,
符合抛物线性质,则M的轨迹是抛物线,
故选:D.
7.圆x2+y2﹣mx+y+m=0在x轴上截得的弦长是它在y轴上截得的弦长的2倍,则实数m的值是( )
A. B. C. D.
解:对于x2+y2﹣mx+y+m=0,
令x=0得:y2+y+m=0,设与y轴交点的纵坐标为y1,y2,且1﹣4m>0,得m①.
则y1+y2=﹣1,y1y2=m,故与y轴相交的弦长为:=.
同理,令y=0可得:x2﹣mx+m=0,设与x轴交点的横坐标为x1,x2,且m2﹣4m>0,得m>4,或m<0②.
则x1+x2=m,x1x2=m,故与x轴相交的弦长为:=.
由题意得:,解得:,结合①②得:m=﹣6符合题意.
故选:A.
8.正三棱锥A﹣BCD中,二面角A﹣BC﹣D的大小为α,二面角B﹣AC﹣D的大小为β,则cos2α+cosβ的取值范围是( )
A. B. C. D.
解:设该正三棱锥的底面边长为2a,
记点A在底面BCD上的投影为点O,连结AO,
则点O为△BCD的中心,AO⊥平面BCD,
因为△BCD为等边三角形,所以O为△BCD的重心,
取BC的中点E,连结DE,AE,
则DE⊥BC,AE⊥BC,OE=,
所以∠AED为二面角A﹣BC﹣D的平面角,即∠AED=α,
记△ABC的高为h,则h=AE>OE=,
所以cosα=cos∠AED=,
过点B作BF⊥AC于点F,连结DE,
由正三棱锥的对称性可得,DF⊥AC,
则∠BFD为二面角B﹣AC﹣D的平面角,即∠BFD=β,
在△ABC中,,
又AC=,所以,
所以cosβ=cos∠BFD===,
因此cos2α+cosβ=,
因为,则,
所以cos2α+cosβ=.
故选:B.
9.曲线C1:y2=6|x|与C2:=1交点的个数为( )
A.1 B.2 C.3 D.4
解:因为曲线C1:y2=6|x|,
所以当x≥0时,y2=6x,
当x<0时,y2=﹣6x,
因为C2:=1,
所以当x≥0,y≥0时,﹣=1,
当x>0,y<0时,﹣﹣=1,无意义,
当x<0,y<0时,﹣+=1,
当x<0,y>0时,+=1,
所以曲线C1与曲线C2共四个交点,
故选:D.
10.在正四面体ABCD中,P,Q分别是棱AB,CD的中点,E,F分别是直线AB,CD上的动点,且满足|PE|+|QF|=a,M是EF的中点,则点M的轨迹围成的区域的面积是( )
A. B. C. D.
解:在正四面体ABCD中,取BC,BD,AD,AC的中点G,H,K,L,如图所示,
因为P,Q分别是棱AB,CD的中点,所以PQ的中点O也为定点,
由对称性可知,PQ和EF的中点都在中截面GHKL(正方形)上,
由,
所以,
设E,F在中截面上的投影分别为E',F',
所以,
所以点M是线段E'F'的中点,
作a∥CD,b∥AB,如图所示,则∠E'OF'=90°,
因为PE+QF=a,所以OE'+OF'=a,
取OR=ON=,则OR+ON=a,
两式相减可得RE'=NF',
过点E'作E'S∥RN,所以RE'=NS,所以RE'=NS'=NF',
所以E'F'的中点M在RN上,
同理E'F'的中点M在NT,TW,WR上,
因为,
故定点M的轨迹是边长为的正方形RNTW,
所以其轨迹围成的区域的面积为.
故选:B.
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
11.已知抛物线C的焦点F(1,0),则拋物线C的标准方程为 y2=4x ,焦点到准线的距离为 2 .
解:由抛物线的定义可知该抛物线开口向右,,
∴抛物线方程为y2=4x,
焦点到准线的距离为2.
故答案为:y2=4x,2.
12.已知某几何体的三视图如图,则该几何体的体积为 7 cm3,表面积为 19+2 cm2.
解:由三视图,可知该几何体为棱长为2的正方体截去一个直三棱柱,
直三棱柱的底面是等腰直角三角形,直角边长为1,高为2,
则该几何体的体积V=;
表面积S=5×=19+.
故答案为:7;19+2.
13.若直线l1:y=kx+1与直线l2关于点(2,3)对称,则直线l2恒过定点 (4,5) ,l1与l2的距离的最大值是 4 .
解:因为l1:y=kx+1经过定点(0,1),∴l2恒过定点(4,5),
∴l1与l2的距离的最大值是=4.
故答案为:(4,5),4.
14.已知P是圆C:(x﹣3)2+(y﹣4)2=1上一动点,过圆心C作两条互相垂直的直线l1,l2,它们分别交x轴于A点,交y轴于B点,记AB中点为Q,则PQ的最小值是 ,圆C上到Q的距离等于3的点有 2 个.
解:(1)易知,圆C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径r=1.
由已知得:CA⊥CB,且OA⊥OB,所以O,A,C,B四点共圆,故Q点为该圆的圆心,
要使|PQ|最小,只需|CQ|最小,显然当O,C,Q三点共线时|CQ|最小,
此时|CQ|=.
所以|PQ|min=.
(2)由上一个问题可知,Q().
所以,以Q为圆心,半径为3的圆Q的方程为:.
因为:|CQ|==,
∴|PQ|min=2.5﹣1=1.5,
|PQ|max=2.5+1=3.5,
∵1.5<3<3.5,
所以圆C上到Q的距离等于3的点有2个.
故答案为:,2.
15.已知平面α∥β,直线l与α所成角的正切值为,直线m?α,l⊥m,直线n?β,且l和n所成角为,那么m与n所成的角为 .
解:如图,
分别平移直线m与n,使得m与l交于A,n与l交于B,
设A在平面β内的射影为A′,则AA′⊥β,
在β内过A′作A′C⊥n,垂足为C,连接AC,可得AC⊥n,
∵直线l与α所成角的正切值为,且α∥β,
∴直线l与β所成角的正切值为,即tan∠ABA′=,
设A′B=1,则AA′=,可得AB=,
又l和n所成角为,∴,又AC⊥BC,
可得AC=BC=,
在Rt△A′CB中,可得cos,则∠A′BC=.
即A′B与n所成角为,
∵AB⊥m,AA′⊥m,AB∩AA′=A,∴m⊥平面AA′B,而A′B?平面AA′B,
∴m⊥A′B,则m与n所成角为.
故答案为:.
16.已知椭圆C:=1,过C上一点P(第一象限)的直线l与x轴正半轴,y轴正半轴分别交于点A,B.若|PA|=1,则|PB|的值为 .
解:如图,
设P(,sinθ),A(a,0),
∵|PA|=1,∴,得a=,
∵△PQB∽△AOB,∴,
则,
设|PB|=m,则|AB|=m+1,
∴,解得m=,
故答案为:.
17.如图,双曲线C1:=1(a>0,b>0)的右焦点F是拋物线C2:y2=2px的焦点,O为坐标原点,A为双曲线C1与拋物线C2在第一象限内的交点,若,则双曲线C1的离心率是 .
解:双曲线C1:=1(a>0,b>0)的右焦点F(c,0),
拋物线C2:y2=2px的焦点F(,0),则c=,即p=2c,
设A(x1,y1),则(x1>0,y1>0),
联立,得b2x2﹣4a2cx=a2b2.
解得x1==
==.
由抛物线的性质,可得,,,
=,
∴,则,
得,
∴.
则,可得=,
即,可得.
可得e=,
∵e>1,∴e=.
故答案为:.
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.已知圆C经过M(1,0),N(2,1)两点,且圆心C在直线x+2y﹣2=0上.
(1)求圆C的方程;
(2)过点P(0,1)的直线l与圆C交于不同的A,B两点,且CA⊥CB,求直线l的方程.
解:(1)由题意设圆C的方程为:x2+y2+Dx+Ey+F=0,
根据圆C经过M(1,0),N(2,1)两点,且圆心C在直线x+2y﹣2=0上可得:
,解得D=﹣4,E=0,F=3.
即圆的方程为:x2+y2﹣4x+3=0.
(2)由(1)知,圆心C(2,0),半径r=1.
由CA⊥CB,可知三角形ABC为等腰直角三角形,故圆心C到直线AB的距离为.
由题意设直线l的方程为:y=kx+1,即kx﹣y+1=0.
故,整理得7k2+8k+1=0,解得k=﹣1,或k=﹣.
故直线l的方程为:y=﹣x+1,或,
即x+y﹣1=0,或x+7y﹣7=0.
19.如图,已知三棱锥P﹣ABC中,AB=BC=2,PA=PC=PB=,且AB⊥BC.
(1)求证:AC⊥PB;
(2)求二面角P﹣BC﹣A的大小.
【解答】证明:(1)取AC的中点O,连接BO,PO,
∵AB=BC,∴BO⊥AC,
又PA=PC,∴PO⊥AC,
而PO∩BO=O,∴AC⊥平面POB,
又PB?平面POB,∴AC⊥PB;
解:(2)在△ABC中,∵AB=BC=2,且AB⊥BC,
∴AC=,则BO=,
在△PAC中,由PA=PC=,AC=,可得PO=,
又PB=,∴PO2+BO2=PB2,得PO⊥BO,
又PO⊥AC,AC∩BO=O,AC、BO?平面ABC,
∴PO⊥平面ABC,在平面ABC中,过O作OD⊥BC,垂足为D,
连接PD,由三垂线定理可得,PD⊥BC,则∠PDO为二面角P﹣BC﹣A的平面角,
由AB⊥BC,OD⊥BC,O为AC的中点,可得OD=AB=1.
在Rt△POD中,由PO=1,OD=1,得△POD为等腰直角三角形,
则∠PDO=.
故二面角P﹣BC﹣A的大小为.
20.如图,已知椭圆的离心率为,且过点.
(1)求椭圆C的标准方程;
(2)过左焦点F且斜率为正的直线l与椭圆C交于A、B两点,过点A、B分别作与直线l垂直的直线,交x轴于C、D两点,求|FC|?|FD|的最小值.
解:(1)根据题意可得,
解得a=2,b=1,c=,
所以椭圆的方程为+y2=1.
(2)设直线l的方程为x=my﹣,A(x1,y1),B(x2,y2),
联立,得(4+m2)y2﹣2my﹣1=0,
所以y1+y2=,y1y2=﹣,
所以|AF|===|y1|,
同理可得|BF|=|y2|,
因为△AFC∽△BFD,
所以==,
因为直线AB斜率为,
所以tan∠BFD==,
所以|BD|==|y2|,
所以|DF|==|y2|,
所以=,
所以|CF|=?|DF|=?|y1|,
所以|FC|?|FD|===,
当t=3时,取最小值=,
所以|FC|?|FD|最小值为.
21.在三棱台ABC﹣DEF中,AB=BC=2DE,∠DAB=∠EBA=60°,平面ABED⊥平面ABC,BC⊥BE.
(1)求证:平面ABED⊥平面BCFE;
(2)求直线DF与平面ABF所成角的正弦值.
【解答】(1)证明:过点E作EH⊥AB于H,
∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EH?平面ABED,
∴EH⊥平面ABC,
∵BC?平面ABC,
∴EH⊥BC,
又BC⊥BE,BE、EH?平面ABED,
∴BC⊥平面ABED,
∵BC?平面BCFE,
∴平面ABED⊥平面BCFE.
(2)解:将三棱台ABC﹣DEF补成三棱锥P﹣ABC,
∵AB=2DE,∠DAB=∠EBA=60°,
∴D,E,F分别为PA,PB,PC的中点,且△PAB为正三角形,
以B为原点,BC,BA所在直线分别为x,y轴,作Bz⊥平面ABC,建立如图所示的空间直角坐标系,
设AB=2,则A(0,2,0),P(0,1,),C(2,0,0),D(0,,),F(1,,),
∴=(1,﹣1,0),=(0,2,0),=(1,,),
设平面ABF的法向量为=(x,y,z),则,即,
令z=2,则x=﹣,y=0,∴=(﹣,0,2),
设直线DF与平面ABF所成角为θ,则sinθ=|cos<,>|=||=||=,
故直线DF与平面ABF所成角的正弦值为.
22.如图,已知过拋物线C:y2=4x的焦点F的直线交抛物线C于点A,B(点A在第一象限),线段AB的中点为M,拋物线C在点A处的切线与以AM为直径的圆交于另一点P.
(1)若,求直线AB的方程;
(2)试问是否为定值?若是,请求出该定值;若不是,请求出它的最大值.
解:(1)拋物线C:y2=4x的焦点F(1,0),=(1﹣xA,﹣yA),=(xB﹣1,yB),
因为,则1﹣xA=4(xB﹣1),①,﹣yA=4yB,②,又yA2=4xA,③,yB2=4xB,④,
由①②③④解得A(4,4),B(,﹣1),所以kAB==,
则AB的方程为y﹣4=(x﹣4),化为4x﹣3y﹣4=0;
(2)设AB的方程为x=my+1,A(,y1),B(,y2),
由可得y2﹣4my﹣4=0,
则y1+y2=4m,y1y2=﹣4,
由y2=4x,两边对x求得可得2yy′=4,即y′=,
可得抛物线在A处的切线的斜率为,
设A点处的切线的方程为x﹣=(y﹣y1),
化为x=﹣,AP与y轴的交点为Q(0,),
=(﹣,﹣),==(,(y2﹣y1)),
因为AM为直径,P在圆上,所以AP⊥PM,
即有|AP|==,
所以|AB|?|AF|=?=((y22﹣y12),y2﹣y1)?(1﹣,﹣y1)==,
又|AP|2=,
所以为定值.
一、选择题(共10小题).
1.直线x+y﹣1=0的倾斜角为( )
A.30° B.60° C.120° D.150°
2.直线2x+3y=0是双曲线的一条渐近线,则实数a的值为( )
A. B.3 C. D.
3.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
A.若m∥n,n?α,则m∥α B.若m∥α,m∥β,则α∥β
C.若m⊥α,n⊥α,则m∥n D.若α⊥γ,β⊥γ,则α∥β
4.“m=﹣1”是“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.在四面体O﹣ABC中,点P为棱BC的中点.设,,,那么向量用基底{,,}可表示为( )
A. B.
C. D.
6.已知平面α和两条异面直线a,b满足a?α,b⊥α,平面α内的动点M到两条直线a,b的距离相等,则点M的轨迹是( )
A.两条直线 B.椭圆 C.双曲线 D.抛物线
7.圆x2+y2﹣mx+y+m=0在x轴上截得的弦长是它在y轴上截得的弦长的2倍,则实数m的值是( )
A. B. C. D.
8.正三棱锥A﹣BCD中,二面角A﹣BC﹣D的大小为α,二面角B﹣AC﹣D的大小为β,则cos2α+cosβ的取值范围是( )
A. B. C. D.
9.曲线C1:y2=6|x|与C2:=1交点的个数为( )
A.1 B.2 C.3 D.4
10.在正四面体ABCD中,P,Q分别是棱AB,CD的中点,E,F分别是直线AB,CD上的动点,且满足|PE|+|QF|=a,M是EF的中点,则点M的轨迹围成的区域的面积是( )
A. B. C. D.
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
11.已知抛物线C的焦点F(1,0),则拋物线C的标准方程为 ,焦点到准线的距离为 .
12.已知某几何体的三视图如图,则该几何体的体积为 cm3,表面积为 cm2.
13.若直线l1:y=kx+1与直线l2关于点(2,3)对称,则直线l2恒过定点 ,l1与l2的距离的最大值是 .
14.已知P是圆C:(x﹣3)2+(y﹣4)2=1上一动点,过圆心C作两条互相垂直的直线l1,l2,它们分别交x轴于A点,交y轴于B点,记AB中点为Q,则PQ的最小值是 ,圆C上到Q的距离等于3的点有 个.
15.已知平面α∥β,直线l与α所成角的正切值为,直线m?α,l⊥m,直线n?β,且l和n所成角为,那么m与n所成的角为 .
16.已知椭圆C:=1,过C上一点P(第一象限)的直线l与x轴正半轴,y轴正半轴分别交于点A,B.若|PA|=1,则|PB|的值为 .
17.如图,双曲线C1:=1(a>0,b>0)的右焦点F是拋物线C2:y2=2px的焦点,O为坐标原点,A为双曲线C1与拋物线C2在第一象限内的交点,若,则双曲线C1的离心率是 .
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.已知圆C经过M(1,0),N(2,1)两点,且圆心C在直线x+2y﹣2=0上.
(1)求圆C的方程;
(2)过点P(0,1)的直线l与圆C交于不同的A,B两点,且CA⊥CB,求直线l的方程.
19.如图,已知三棱锥P﹣ABC中,AB=BC=2,PA=PC=PB=,且AB⊥BC.
(1)求证:AC⊥PB;
(2)求二面角P﹣BC﹣A的大小.
20.如图,已知椭圆的离心率为,且过点.
(1)求椭圆C的标准方程;
(2)过左焦点F且斜率为正的直线l与椭圆C交于A、B两点,过点A、B分别作与直线l垂直的直线,交x轴于C、D两点,求|FC|?|FD|的最小值.
21.在三棱台ABC﹣DEF中,AB=BC=2DE,∠DAB=∠EBA=60°,平面ABED⊥平面ABC,BC⊥BE.
(1)求证:平面ABED⊥平面BCFE;
(2)求直线DF与平面ABF所成角的正弦值.
22.如图,已知过拋物线C:y2=4x的焦点F的直线交抛物线C于点A,B(点A在第一象限),线段AB的中点为M,拋物线C在点A处的切线与以AM为直径的圆交于另一点P.
(1)若,求直线AB的方程;
(2)试问是否为定值?若是,请求出该定值;若不是,请求出它的最大值.
参考答案
一、选择题(共10小题).
1.直线x+y﹣1=0的倾斜角为( )
A.30° B.60° C.120° D.150°
解:设直线x+y﹣1=0的倾斜角为α.
直线x+y﹣1=0化为.
∴tanα=﹣.
∵α∈[0°,180°),
∴α=150°.
故选:D.
2.直线2x+3y=0是双曲线的一条渐近线,则实数a的值为( )
A. B.3 C. D.
解:双曲线的渐近线方程为,化为2x±ay=0,
又2x+3y=0是双曲线的一条渐近线,∴a=3.
故选:B.
3.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
A.若m∥n,n?α,则m∥α B.若m∥α,m∥β,则α∥β
C.若m⊥α,n⊥α,则m∥n D.若α⊥γ,β⊥γ,则α∥β
解:若m∥n,n?α,且m?α,则m∥α,故A错误;
若m∥α,m∥β,则α∥β,或α、β相交,故B错误;
若m⊥α,n⊥α,则m∥n,故C正确;
若α⊥γ,β⊥γ,则α∥β,或α、β相交,故D错误.
故选:C.
4.“m=﹣1”是“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”?2m+m(m﹣1)=0,解得m=0,或m=﹣1.
∴“m=﹣1”是“直线mx+(m﹣1)y+1=0和直线2x+my+3=0垂直”的充分不必要条件.
故选:A.
5.在四面体O﹣ABC中,点P为棱BC的中点.设,,,那么向量用基底{,,}可表示为( )
A. B.
C. D.
解:∵点P为棱BC的中点,
∴=(+),
∴==(+)﹣,
又∵,,,
∴=(+)﹣=﹣++.
故选:B.
6.已知平面α和两条异面直线a,b满足a?α,b⊥α,平面α内的动点M到两条直线a,b的距离相等,则点M的轨迹是( )
A.两条直线 B.椭圆 C.双曲线 D.抛物线
解:b⊥α,设垂足为B,则M到直线b的距离即为M到定点B的距离,
即动点M在平面α内到一定直线距离与一定点的距离相等,
符合抛物线性质,则M的轨迹是抛物线,
故选:D.
7.圆x2+y2﹣mx+y+m=0在x轴上截得的弦长是它在y轴上截得的弦长的2倍,则实数m的值是( )
A. B. C. D.
解:对于x2+y2﹣mx+y+m=0,
令x=0得:y2+y+m=0,设与y轴交点的纵坐标为y1,y2,且1﹣4m>0,得m①.
则y1+y2=﹣1,y1y2=m,故与y轴相交的弦长为:=.
同理,令y=0可得:x2﹣mx+m=0,设与x轴交点的横坐标为x1,x2,且m2﹣4m>0,得m>4,或m<0②.
则x1+x2=m,x1x2=m,故与x轴相交的弦长为:=.
由题意得:,解得:,结合①②得:m=﹣6符合题意.
故选:A.
8.正三棱锥A﹣BCD中,二面角A﹣BC﹣D的大小为α,二面角B﹣AC﹣D的大小为β,则cos2α+cosβ的取值范围是( )
A. B. C. D.
解:设该正三棱锥的底面边长为2a,
记点A在底面BCD上的投影为点O,连结AO,
则点O为△BCD的中心,AO⊥平面BCD,
因为△BCD为等边三角形,所以O为△BCD的重心,
取BC的中点E,连结DE,AE,
则DE⊥BC,AE⊥BC,OE=,
所以∠AED为二面角A﹣BC﹣D的平面角,即∠AED=α,
记△ABC的高为h,则h=AE>OE=,
所以cosα=cos∠AED=,
过点B作BF⊥AC于点F,连结DE,
由正三棱锥的对称性可得,DF⊥AC,
则∠BFD为二面角B﹣AC﹣D的平面角,即∠BFD=β,
在△ABC中,,
又AC=,所以,
所以cosβ=cos∠BFD===,
因此cos2α+cosβ=,
因为,则,
所以cos2α+cosβ=.
故选:B.
9.曲线C1:y2=6|x|与C2:=1交点的个数为( )
A.1 B.2 C.3 D.4
解:因为曲线C1:y2=6|x|,
所以当x≥0时,y2=6x,
当x<0时,y2=﹣6x,
因为C2:=1,
所以当x≥0,y≥0时,﹣=1,
当x>0,y<0时,﹣﹣=1,无意义,
当x<0,y<0时,﹣+=1,
当x<0,y>0时,+=1,
所以曲线C1与曲线C2共四个交点,
故选:D.
10.在正四面体ABCD中,P,Q分别是棱AB,CD的中点,E,F分别是直线AB,CD上的动点,且满足|PE|+|QF|=a,M是EF的中点,则点M的轨迹围成的区域的面积是( )
A. B. C. D.
解:在正四面体ABCD中,取BC,BD,AD,AC的中点G,H,K,L,如图所示,
因为P,Q分别是棱AB,CD的中点,所以PQ的中点O也为定点,
由对称性可知,PQ和EF的中点都在中截面GHKL(正方形)上,
由,
所以,
设E,F在中截面上的投影分别为E',F',
所以,
所以点M是线段E'F'的中点,
作a∥CD,b∥AB,如图所示,则∠E'OF'=90°,
因为PE+QF=a,所以OE'+OF'=a,
取OR=ON=,则OR+ON=a,
两式相减可得RE'=NF',
过点E'作E'S∥RN,所以RE'=NS,所以RE'=NS'=NF',
所以E'F'的中点M在RN上,
同理E'F'的中点M在NT,TW,WR上,
因为,
故定点M的轨迹是边长为的正方形RNTW,
所以其轨迹围成的区域的面积为.
故选:B.
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
11.已知抛物线C的焦点F(1,0),则拋物线C的标准方程为 y2=4x ,焦点到准线的距离为 2 .
解:由抛物线的定义可知该抛物线开口向右,,
∴抛物线方程为y2=4x,
焦点到准线的距离为2.
故答案为:y2=4x,2.
12.已知某几何体的三视图如图,则该几何体的体积为 7 cm3,表面积为 19+2 cm2.
解:由三视图,可知该几何体为棱长为2的正方体截去一个直三棱柱,
直三棱柱的底面是等腰直角三角形,直角边长为1,高为2,
则该几何体的体积V=;
表面积S=5×=19+.
故答案为:7;19+2.
13.若直线l1:y=kx+1与直线l2关于点(2,3)对称,则直线l2恒过定点 (4,5) ,l1与l2的距离的最大值是 4 .
解:因为l1:y=kx+1经过定点(0,1),∴l2恒过定点(4,5),
∴l1与l2的距离的最大值是=4.
故答案为:(4,5),4.
14.已知P是圆C:(x﹣3)2+(y﹣4)2=1上一动点,过圆心C作两条互相垂直的直线l1,l2,它们分别交x轴于A点,交y轴于B点,记AB中点为Q,则PQ的最小值是 ,圆C上到Q的距离等于3的点有 2 个.
解:(1)易知,圆C:(x﹣3)2+(y﹣4)2=1的圆心C(3,4),半径r=1.
由已知得:CA⊥CB,且OA⊥OB,所以O,A,C,B四点共圆,故Q点为该圆的圆心,
要使|PQ|最小,只需|CQ|最小,显然当O,C,Q三点共线时|CQ|最小,
此时|CQ|=.
所以|PQ|min=.
(2)由上一个问题可知,Q().
所以,以Q为圆心,半径为3的圆Q的方程为:.
因为:|CQ|==,
∴|PQ|min=2.5﹣1=1.5,
|PQ|max=2.5+1=3.5,
∵1.5<3<3.5,
所以圆C上到Q的距离等于3的点有2个.
故答案为:,2.
15.已知平面α∥β,直线l与α所成角的正切值为,直线m?α,l⊥m,直线n?β,且l和n所成角为,那么m与n所成的角为 .
解:如图,
分别平移直线m与n,使得m与l交于A,n与l交于B,
设A在平面β内的射影为A′,则AA′⊥β,
在β内过A′作A′C⊥n,垂足为C,连接AC,可得AC⊥n,
∵直线l与α所成角的正切值为,且α∥β,
∴直线l与β所成角的正切值为,即tan∠ABA′=,
设A′B=1,则AA′=,可得AB=,
又l和n所成角为,∴,又AC⊥BC,
可得AC=BC=,
在Rt△A′CB中,可得cos,则∠A′BC=.
即A′B与n所成角为,
∵AB⊥m,AA′⊥m,AB∩AA′=A,∴m⊥平面AA′B,而A′B?平面AA′B,
∴m⊥A′B,则m与n所成角为.
故答案为:.
16.已知椭圆C:=1,过C上一点P(第一象限)的直线l与x轴正半轴,y轴正半轴分别交于点A,B.若|PA|=1,则|PB|的值为 .
解:如图,
设P(,sinθ),A(a,0),
∵|PA|=1,∴,得a=,
∵△PQB∽△AOB,∴,
则,
设|PB|=m,则|AB|=m+1,
∴,解得m=,
故答案为:.
17.如图,双曲线C1:=1(a>0,b>0)的右焦点F是拋物线C2:y2=2px的焦点,O为坐标原点,A为双曲线C1与拋物线C2在第一象限内的交点,若,则双曲线C1的离心率是 .
解:双曲线C1:=1(a>0,b>0)的右焦点F(c,0),
拋物线C2:y2=2px的焦点F(,0),则c=,即p=2c,
设A(x1,y1),则(x1>0,y1>0),
联立,得b2x2﹣4a2cx=a2b2.
解得x1==
==.
由抛物线的性质,可得,,,
=,
∴,则,
得,
∴.
则,可得=,
即,可得.
可得e=,
∵e>1,∴e=.
故答案为:.
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.已知圆C经过M(1,0),N(2,1)两点,且圆心C在直线x+2y﹣2=0上.
(1)求圆C的方程;
(2)过点P(0,1)的直线l与圆C交于不同的A,B两点,且CA⊥CB,求直线l的方程.
解:(1)由题意设圆C的方程为:x2+y2+Dx+Ey+F=0,
根据圆C经过M(1,0),N(2,1)两点,且圆心C在直线x+2y﹣2=0上可得:
,解得D=﹣4,E=0,F=3.
即圆的方程为:x2+y2﹣4x+3=0.
(2)由(1)知,圆心C(2,0),半径r=1.
由CA⊥CB,可知三角形ABC为等腰直角三角形,故圆心C到直线AB的距离为.
由题意设直线l的方程为:y=kx+1,即kx﹣y+1=0.
故,整理得7k2+8k+1=0,解得k=﹣1,或k=﹣.
故直线l的方程为:y=﹣x+1,或,
即x+y﹣1=0,或x+7y﹣7=0.
19.如图,已知三棱锥P﹣ABC中,AB=BC=2,PA=PC=PB=,且AB⊥BC.
(1)求证:AC⊥PB;
(2)求二面角P﹣BC﹣A的大小.
【解答】证明:(1)取AC的中点O,连接BO,PO,
∵AB=BC,∴BO⊥AC,
又PA=PC,∴PO⊥AC,
而PO∩BO=O,∴AC⊥平面POB,
又PB?平面POB,∴AC⊥PB;
解:(2)在△ABC中,∵AB=BC=2,且AB⊥BC,
∴AC=,则BO=,
在△PAC中,由PA=PC=,AC=,可得PO=,
又PB=,∴PO2+BO2=PB2,得PO⊥BO,
又PO⊥AC,AC∩BO=O,AC、BO?平面ABC,
∴PO⊥平面ABC,在平面ABC中,过O作OD⊥BC,垂足为D,
连接PD,由三垂线定理可得,PD⊥BC,则∠PDO为二面角P﹣BC﹣A的平面角,
由AB⊥BC,OD⊥BC,O为AC的中点,可得OD=AB=1.
在Rt△POD中,由PO=1,OD=1,得△POD为等腰直角三角形,
则∠PDO=.
故二面角P﹣BC﹣A的大小为.
20.如图,已知椭圆的离心率为,且过点.
(1)求椭圆C的标准方程;
(2)过左焦点F且斜率为正的直线l与椭圆C交于A、B两点,过点A、B分别作与直线l垂直的直线,交x轴于C、D两点,求|FC|?|FD|的最小值.
解:(1)根据题意可得,
解得a=2,b=1,c=,
所以椭圆的方程为+y2=1.
(2)设直线l的方程为x=my﹣,A(x1,y1),B(x2,y2),
联立,得(4+m2)y2﹣2my﹣1=0,
所以y1+y2=,y1y2=﹣,
所以|AF|===|y1|,
同理可得|BF|=|y2|,
因为△AFC∽△BFD,
所以==,
因为直线AB斜率为,
所以tan∠BFD==,
所以|BD|==|y2|,
所以|DF|==|y2|,
所以=,
所以|CF|=?|DF|=?|y1|,
所以|FC|?|FD|===,
当t=3时,取最小值=,
所以|FC|?|FD|最小值为.
21.在三棱台ABC﹣DEF中,AB=BC=2DE,∠DAB=∠EBA=60°,平面ABED⊥平面ABC,BC⊥BE.
(1)求证:平面ABED⊥平面BCFE;
(2)求直线DF与平面ABF所成角的正弦值.
【解答】(1)证明:过点E作EH⊥AB于H,
∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EH?平面ABED,
∴EH⊥平面ABC,
∵BC?平面ABC,
∴EH⊥BC,
又BC⊥BE,BE、EH?平面ABED,
∴BC⊥平面ABED,
∵BC?平面BCFE,
∴平面ABED⊥平面BCFE.
(2)解:将三棱台ABC﹣DEF补成三棱锥P﹣ABC,
∵AB=2DE,∠DAB=∠EBA=60°,
∴D,E,F分别为PA,PB,PC的中点,且△PAB为正三角形,
以B为原点,BC,BA所在直线分别为x,y轴,作Bz⊥平面ABC,建立如图所示的空间直角坐标系,
设AB=2,则A(0,2,0),P(0,1,),C(2,0,0),D(0,,),F(1,,),
∴=(1,﹣1,0),=(0,2,0),=(1,,),
设平面ABF的法向量为=(x,y,z),则,即,
令z=2,则x=﹣,y=0,∴=(﹣,0,2),
设直线DF与平面ABF所成角为θ,则sinθ=|cos<,>|=||=||=,
故直线DF与平面ABF所成角的正弦值为.
22.如图,已知过拋物线C:y2=4x的焦点F的直线交抛物线C于点A,B(点A在第一象限),线段AB的中点为M,拋物线C在点A处的切线与以AM为直径的圆交于另一点P.
(1)若,求直线AB的方程;
(2)试问是否为定值?若是,请求出该定值;若不是,请求出它的最大值.
解:(1)拋物线C:y2=4x的焦点F(1,0),=(1﹣xA,﹣yA),=(xB﹣1,yB),
因为,则1﹣xA=4(xB﹣1),①,﹣yA=4yB,②,又yA2=4xA,③,yB2=4xB,④,
由①②③④解得A(4,4),B(,﹣1),所以kAB==,
则AB的方程为y﹣4=(x﹣4),化为4x﹣3y﹣4=0;
(2)设AB的方程为x=my+1,A(,y1),B(,y2),
由可得y2﹣4my﹣4=0,
则y1+y2=4m,y1y2=﹣4,
由y2=4x,两边对x求得可得2yy′=4,即y′=,
可得抛物线在A处的切线的斜率为,
设A点处的切线的方程为x﹣=(y﹣y1),
化为x=﹣,AP与y轴的交点为Q(0,),
=(﹣,﹣),==(,(y2﹣y1)),
因为AM为直径,P在圆上,所以AP⊥PM,
即有|AP|==,
所以|AB|?|AF|=?=((y22﹣y12),y2﹣y1)?(1﹣,﹣y1)==,
又|AP|2=,
所以为定值.
同课章节目录
