2020-2021学年江西省南昌高一(下)开学数学试卷(Word解析版)
文档属性
| 名称 | 2020-2021学年江西省南昌高一(下)开学数学试卷(Word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览




文档简介
2020-2021学年江西省南昌高一(下)开学数学试卷
一、单项选择题(共12小题).
1.函数f(x)=的定义域是( )
A.(0.e) B.(0,e] C.[e,+∞) D.(e,+∞)
2.已知sin(π+α)=,则sin(+2α)=( )
A. B. C. D.
3.已知,,c=ln3,则( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
4.若单位向量,满足,则向量,夹角的余弦值为( )
A. B. C. D.
5.函数的图象大致是( )
A. B.
C. D.
6.已知函数,若f(m)+2f(﹣m)>0,则实数m的取值范围为( )
A.(﹣∞,﹣1)∪(1,+∞) B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣e)∪(0,e) D.(﹣∞,﹣1)∪(0,1)
7.已知函数f(x)=cosx(x∈(0,π))的图象与函数y=tanx的图象交于A,B两点,则△OAB(O为坐标原点)的面积为( )
A. B. C. D.
8.已知函数是偶函数,则f(x)在上是减函数的一个θ值是( )
A. B. C. D.
9.已知、是平面内两个互相垂直的单位向量,若向量满足(﹣)?(﹣)=0,则||的最大值是( )
A.1 B.2 C. D.
10.设函数f(x)=asinx+bcosx,其中a,b∈R,ab≠0,若f(x)≥f()对一切x∈R恒成立,则下列结论中正确的是( )
A.f()=0
B.点(,0)是函数f(x)的一个对称中心
C.f(x)在(0,)上是增函数
D.存在直线经过点(a,b)且与函数f(x)的图象有无数多个交点
11.已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在线段AB上(不包含两个端点),则的取值范围是( )
A. B.[﹣1,1) C. D.[﹣1,0)
12.已知函数f(x)=的图象上关于y轴对称的点至少有3对,则实数a的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
13.已知函数y=ax﹣3+1(a>0且a≠1)图象恒过定点A在角α的终边上,则tan2α= .
14.如图,在同一个平面内.向量,,的模分别为1,,,与的夹角为α,且,与的夹角为45°.若,则m﹣n= .
15.△ABC的三个内角为A、B、C,当A为 °时,取得最大值,且这个最大值为 .
16.已知函数(ω>0)在内恰有两个最小值点,则ω的取值范围是 .
三、解答题(本大题共7小题,共70分)
17.已知tan(π+α)=3,求的值.
18.已知,求的值.
19.已知向量与的夹角为60°,||=3,||=2,=2﹣3,=3+k.
(Ⅰ)若,求实数k的值;
(Ⅱ)是否存在实数k,使得∥?说明理由.
20.如图是函数一个周期内的图象,已知点是图象与x轴的交点.点C是图象上的最高点,点C的横坐标为.
(1)求函数f(x)的解析式;
(2)记∠ACB=θ,求tanθ的值.
21.如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
(1)设,将用λ、、表示;
(2)设,,证明:是定值.
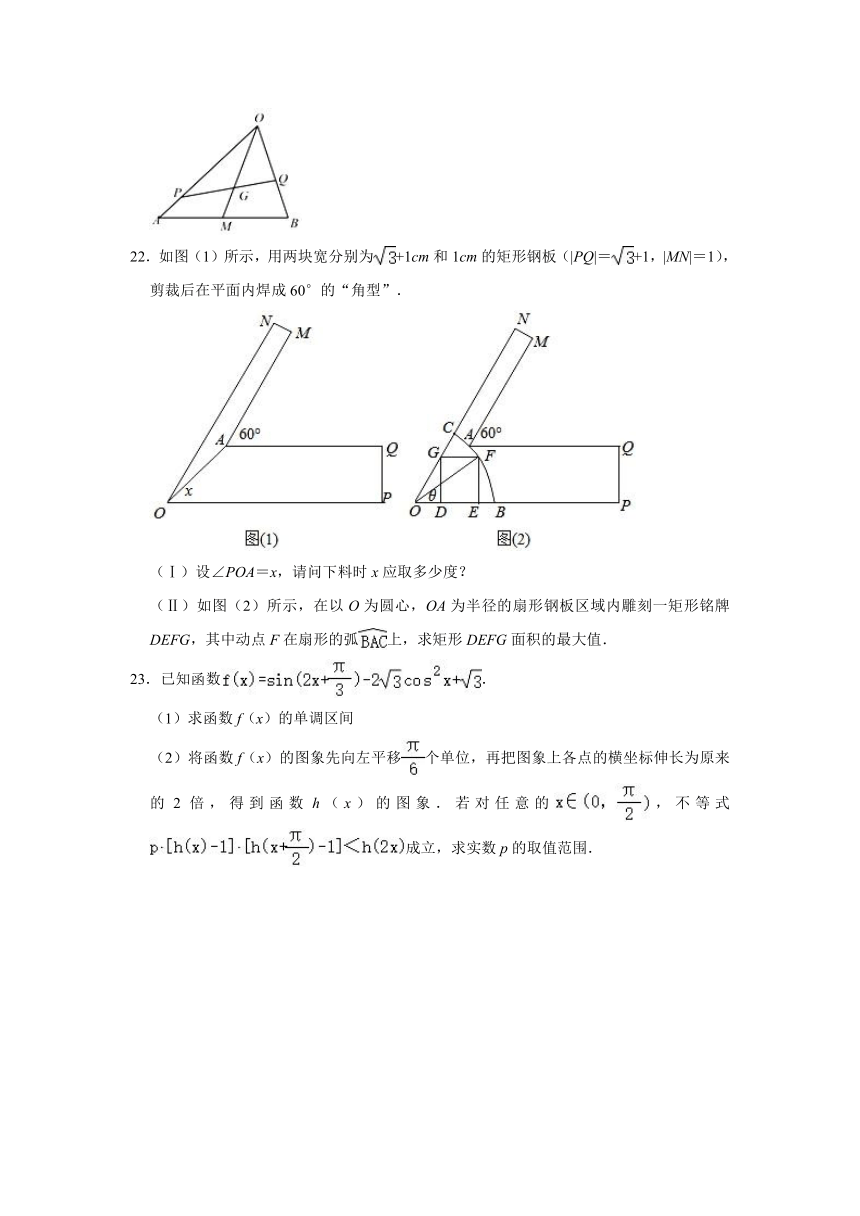
22.如图(1)所示,用两块宽分别为+1cm和1cm的矩形钢板(|PQ|=+1,|MN|=1),剪裁后在平面内焊成60°的“角型”.
(Ⅰ)设∠POA=x,请问下料时x应取多少度?
(Ⅱ)如图(2)所示,在以O为圆心,OA为半径的扇形钢板区域内雕刻一矩形铭牌DEFG,其中动点F在扇形的弧上,求矩形DEFG面积的最大值.
23.已知函数.
(1)求函数f(x)的单调区间
(2)将函数f(x)的图象先向左平移个单位,再把图象上各点的横坐标伸长为原来的2倍,得到函数h(x)的图象.若对任意的,不等式成立,求实数p的取值范围.
参考答案
一、单项选择题(共60分)
1.函数f(x)=的定义域是( )
A.(0.e) B.(0,e] C.[e,+∞) D.(e,+∞)
解:函数f(x)=的定义域的定义域为:
解得0<x≤e.
故函数的定义域为:(0,e],
故选:B.
2.已知sin(π+α)=,则sin(+2α)=( )
A. B. C. D.
解:由,得,
∴==.
故选:A.
3.已知,,c=ln3,则( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
解:a==,b==,
又因为,
所以,
即a<b,
又c=ln3>lne=1,
即a<b<c.
故选:A.
4.若单位向量,满足,则向量,夹角的余弦值为( )
A. B. C. D.
解:根据题意,设向量,夹角为θ,
若单位向量,满足,
则有(2+)2=42+2+4?=5+4cosθ=8,
则有cosθ=,
故选:A.
5.函数的图象大致是( )
A. B.
C. D.
解:函数
满足f(﹣x)=﹣f(x),
故函数图象关于原点对称,排除A、B,
当x∈(0,)时,,
故排除D,
故选:C.
6.已知函数,若f(m)+2f(﹣m)>0,则实数m的取值范围为( )
A.(﹣∞,﹣1)∪(1,+∞) B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣e)∪(0,e) D.(﹣∞,﹣1)∪(0,1)
解:当m>0时则﹣m<0,所以f(m)+2f(﹣m)=lnm﹣2ln(﹣m)>0,
即lnm﹣lnm2=ln>0,解得0<m<1,
当m<0时,﹣m>0,所以f(m)+2f(﹣m)=﹣ln(﹣m)+2lnm>0,
即ln(﹣m)>0,解得m<﹣1,
综上,实数m的取值范围为:(﹣∞,﹣1)∪(0,1),
故选:D.
7.已知函数f(x)=cosx(x∈(0,π))的图象与函数y=tanx的图象交于A,B两点,则△OAB(O为坐标原点)的面积为( )
A. B. C. D.
解:由题意有,有,
有,解得sinx=,或 sinx=﹣(舍去),
由x∈(0,π)可得或,
则点A的坐标为,点B的坐标为,
线段AB中点的坐标为,则△OAB的面积为,
故选:B.
8.已知函数是偶函数,则f(x)在上是减函数的一个θ值是( )
A. B. C. D.
解:函数=2sin(2x+θ+)
∵f(x)是偶函数
∴θ+=,k∈Z
得θ=kπ.
又∵f(x)在上是减函数,
则,
可得:,k∈Z.
当k=0时,
可得.
故选:A.
9.已知、是平面内两个互相垂直的单位向量,若向量满足(﹣)?(﹣)=0,则||的最大值是( )
A.1 B.2 C. D.
解:由题意可得?=0,
可得|+|==,
(﹣)?(﹣)=2+?﹣?(+)
=||2﹣||?|+|cos<(+,>=0,
即为||=cos<+,>,
当cos<+,>=1即+,同向时,
||的最大值是.
故选:C.
10.设函数f(x)=asinx+bcosx,其中a,b∈R,ab≠0,若f(x)≥f()对一切x∈R恒成立,则下列结论中正确的是( )
A.f()=0
B.点(,0)是函数f(x)的一个对称中心
C.f(x)在(0,)上是增函数
D.存在直线经过点(a,b)且与函数f(x)的图象有无数多个交点
解:函数f(x)=asinx+bcosx=sin(x+φ),sinφ,
周期T=2π.
由题意么x=取得最小值,a,b∈R,ab≠0,
∴f()=0不正确;
x=取得最小值,
那么就是相邻的对称中点,
∴点(,0)不是函数f(x)的一个对称中心;
因为x=取得最小值,根据正弦函数的性质可知,f(x)在(0,)是减函数.
故选:D.
11.已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在线段AB上(不包含两个端点),则的取值范围是( )
A. B.[﹣1,1) C. D.[﹣1,0)
解:∵A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在线段AB上(不包含两个端点),
∴,
∴,即,
又∵0<λ<1,∠AOB=120°,
∴点C在线段AB上,且,
∴=,
∵,
∴.
故选:C.
12.已知函数f(x)=的图象上关于y轴对称的点至少有3对,则实数a的取值范围是( )
A. B. C. D.
解:若x>0,则﹣x<0,
∵x<0时,f(x)=sin(x)﹣1,
∴f(﹣x)=sin(﹣x)﹣1=﹣sin(x)﹣1,
则若f(x)=sin(x)﹣1,(x<0)关于y轴对称,
则f(﹣x)=﹣sin(x)﹣1=f(x),
即y=﹣sin(x)﹣1,x>0,
设g(x)=﹣sin(x)﹣1,x>0
作出函数g(x)的图象,
要使y=﹣sin(x)﹣1,x>0与f(x)=logax,x>0的图象至少有3个交点,
则0<a<1且满足g(5)<f(5),
即﹣2<loga5,
即loga5>logaa﹣2,
则5<,
解得0<a<,
故选:D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知函数y=ax﹣3+1(a>0且a≠1)图象恒过定点A在角α的终边上,则tan2α= .
解:∵y=3x﹣3+1恒过点A(3,4),
∴tanα=,
∴tan2==.
故答案为:.
14.如图,在同一个平面内.向量,,的模分别为1,,,与的夹角为α,且,与的夹角为45°.若,则m﹣n= .
解:以O为坐标原点.向量方向为x轴,与向量垂直的方向为y轴,建立平面直角坐标系.
点A的坐标为(1,0),,,
可得点C的坐标为(2,1),,
所以,,
又点B的坐标为(1,3),.,
若,则m+n=2且3n=1,
所以,所以.
故答案为:.
15.△ABC的三个内角为A、B、C,当A为 60 °时,取得最大值,且这个最大值为 .
解:因为A+B+C=180°,则=1﹣2+2cos(﹣)=1﹣2+2sin=﹣2+,
所以当sin=,因为为锐角,所以=30°
即A=60°时,原式的最大值为.
故答案为:60,
16.已知函数(ω>0)在内恰有两个最小值点,则ω的取值范围是 .
解:作出函数(ω>0)的图象,
=,,
要使在内恰有两个最小值点,
所以,解得,即.
故答案为:.
三、解答题(本大题共7小题,共70分)
17.已知tan(π+α)=3,求的值.
解:∵tan(π+α)=tanα=3,
∴原式====7.
18.已知,求的值.
【解答】解∵,,
∴,
∴原式=
=
=
=.
19.已知向量与的夹角为60°,||=3,||=2,=2﹣3,=3+k.
(Ⅰ)若,求实数k的值;
(Ⅱ)是否存在实数k,使得∥?说明理由.
解:(Ⅰ)向量与的夹角为60°,||=3,||=2,=2﹣3,=3+k,
∴?=(2﹣3)?(3+k)=6||2﹣3k||2+(2k﹣9)?||?||?cos60°=54﹣12k+3(2k﹣9)=0,
解得k=;
(Ⅱ)∵∥,
∴存在实数λ可得(2﹣3)=λ(3+k),
∴,解得k=﹣.
20.如图是函数一个周期内的图象,已知点是图象与x轴的交点.点C是图象上的最高点,点C的横坐标为.
(1)求函数f(x)的解析式;
(2)记∠ACB=θ,求tanθ的值.
解:(1)由图可知,函数f(x)的周期为,
∴.
代入点C的坐标,有.
又由,可得,
可得,有,
故函数f(x)的解析式为.
(2)如图.过点C作x轴的垂线,垂足为M.
可得点M的坐标为,
由函数f(x)图象的周期性,可得点B的坐标为,|,,|CM|=1,
在△AMC中,,
在△BMC中,,,
由θ=π﹣(∠CAM+∠CBM).
可得 tanθ=﹣tan(∠CAM+∠CBM)=8,故tanθ=8.
21.如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
(1)设,将用λ、、表示;
(2)设,,证明:是定值.
解:(1)∵,
∴,即=λ()
整理,得=(1﹣λ)+λ
(2)∵G是△OAB的重心,
∴==×(+)=(+)
∵,,=(1﹣λ)+λ
∴=(1﹣λ)+λ
因此,得到,可得,
∴=3(1﹣λ)+3λ=3,即=3(定值).
22.如图(1)所示,用两块宽分别为+1cm和1cm的矩形钢板(|PQ|=+1,|MN|=1),剪裁后在平面内焊成60°的“角型”.
(Ⅰ)设∠POA=x,请问下料时x应取多少度?
(Ⅱ)如图(2)所示,在以O为圆心,OA为半径的扇形钢板区域内雕刻一矩形铭牌DEFG,其中动点F在扇形的弧上,求矩形DEFG面积的最大值.
解:(Ⅰ)过A作AX、AY分别垂直OP、ON于X、Y,则在Rt△OAX与Rt△OAY中,
OA==,
∴=,
∴(+1)sin(60°﹣x)=sinx,
∴sinx=cosx
∴x=45°,
(Ⅱ)由(Ⅰ)知,OF=OA=(+1)×=+,
设∠BOF=θ,EF=OFsinθ=(+)sinθ,
DE=OE﹣OD=OE﹣=(+)cosθ﹣sinθ=(+)(cosθ﹣sinθ),
∴S矩形DEFG=EF?DE=(+)2sinθ(cosθ﹣sinθ)=(+)2[(sin2θ+cos2θ)﹣],
=(+)2[sin(2θ+φ)﹣],
≤(+)2(﹣),
=2+
∴矩形DEFG面积的最大值为2+
23.已知函数.
(1)求函数f(x)的单调区间
(2)将函数f(x)的图象先向左平移个单位,再把图象上各点的横坐标伸长为原来的2倍,得到函数h(x)的图象.若对任意的,不等式成立,求实数p的取值范围.
解:(1)=
==,
由于y=sinθ的单调增区间为,k∈Z,
令,
解得:,
∴f(x)单调增区间为,k∈Z.
(2)由于 ,
向左平移个单位得到 y=的图象,
再将各点横坐标伸长为原来的两倍得:y=的图象,故h(x)=sinx.
不等式,
即 ,即 p?(sinx﹣1)(cosx﹣1)<sin2x,成立.
此时,sinx∈(0,1),cosx∈(0,1),sin2x∈(0,1],
∴(sinx﹣1)(cosx﹣1)>0,sin2x>0,
当p≤0时,不等式恒成立,
当p>0时,,
令=,
∴=,
其中sinx+cosx+sinxcosx+1>0,
∴令F'(x)=0得,sinx=cosx,即,
当时,F'(x)>0,F(x)单调递增,
当时,F'(x)<0,F(x)单调递减,
∴,
∴,即,
综上,.
一、单项选择题(共12小题).
1.函数f(x)=的定义域是( )
A.(0.e) B.(0,e] C.[e,+∞) D.(e,+∞)
2.已知sin(π+α)=,则sin(+2α)=( )
A. B. C. D.
3.已知,,c=ln3,则( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
4.若单位向量,满足,则向量,夹角的余弦值为( )
A. B. C. D.
5.函数的图象大致是( )
A. B.
C. D.
6.已知函数,若f(m)+2f(﹣m)>0,则实数m的取值范围为( )
A.(﹣∞,﹣1)∪(1,+∞) B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣e)∪(0,e) D.(﹣∞,﹣1)∪(0,1)
7.已知函数f(x)=cosx(x∈(0,π))的图象与函数y=tanx的图象交于A,B两点,则△OAB(O为坐标原点)的面积为( )
A. B. C. D.
8.已知函数是偶函数,则f(x)在上是减函数的一个θ值是( )
A. B. C. D.
9.已知、是平面内两个互相垂直的单位向量,若向量满足(﹣)?(﹣)=0,则||的最大值是( )
A.1 B.2 C. D.
10.设函数f(x)=asinx+bcosx,其中a,b∈R,ab≠0,若f(x)≥f()对一切x∈R恒成立,则下列结论中正确的是( )
A.f()=0
B.点(,0)是函数f(x)的一个对称中心
C.f(x)在(0,)上是增函数
D.存在直线经过点(a,b)且与函数f(x)的图象有无数多个交点
11.已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在线段AB上(不包含两个端点),则的取值范围是( )
A. B.[﹣1,1) C. D.[﹣1,0)
12.已知函数f(x)=的图象上关于y轴对称的点至少有3对,则实数a的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
13.已知函数y=ax﹣3+1(a>0且a≠1)图象恒过定点A在角α的终边上,则tan2α= .
14.如图,在同一个平面内.向量,,的模分别为1,,,与的夹角为α,且,与的夹角为45°.若,则m﹣n= .
15.△ABC的三个内角为A、B、C,当A为 °时,取得最大值,且这个最大值为 .
16.已知函数(ω>0)在内恰有两个最小值点,则ω的取值范围是 .
三、解答题(本大题共7小题,共70分)
17.已知tan(π+α)=3,求的值.
18.已知,求的值.
19.已知向量与的夹角为60°,||=3,||=2,=2﹣3,=3+k.
(Ⅰ)若,求实数k的值;
(Ⅱ)是否存在实数k,使得∥?说明理由.
20.如图是函数一个周期内的图象,已知点是图象与x轴的交点.点C是图象上的最高点,点C的横坐标为.
(1)求函数f(x)的解析式;
(2)记∠ACB=θ,求tanθ的值.
21.如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
(1)设,将用λ、、表示;
(2)设,,证明:是定值.
22.如图(1)所示,用两块宽分别为+1cm和1cm的矩形钢板(|PQ|=+1,|MN|=1),剪裁后在平面内焊成60°的“角型”.
(Ⅰ)设∠POA=x,请问下料时x应取多少度?
(Ⅱ)如图(2)所示,在以O为圆心,OA为半径的扇形钢板区域内雕刻一矩形铭牌DEFG,其中动点F在扇形的弧上,求矩形DEFG面积的最大值.
23.已知函数.
(1)求函数f(x)的单调区间
(2)将函数f(x)的图象先向左平移个单位,再把图象上各点的横坐标伸长为原来的2倍,得到函数h(x)的图象.若对任意的,不等式成立,求实数p的取值范围.
参考答案
一、单项选择题(共60分)
1.函数f(x)=的定义域是( )
A.(0.e) B.(0,e] C.[e,+∞) D.(e,+∞)
解:函数f(x)=的定义域的定义域为:
解得0<x≤e.
故函数的定义域为:(0,e],
故选:B.
2.已知sin(π+α)=,则sin(+2α)=( )
A. B. C. D.
解:由,得,
∴==.
故选:A.
3.已知,,c=ln3,则( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
解:a==,b==,
又因为,
所以,
即a<b,
又c=ln3>lne=1,
即a<b<c.
故选:A.
4.若单位向量,满足,则向量,夹角的余弦值为( )
A. B. C. D.
解:根据题意,设向量,夹角为θ,
若单位向量,满足,
则有(2+)2=42+2+4?=5+4cosθ=8,
则有cosθ=,
故选:A.
5.函数的图象大致是( )
A. B.
C. D.
解:函数
满足f(﹣x)=﹣f(x),
故函数图象关于原点对称,排除A、B,
当x∈(0,)时,,
故排除D,
故选:C.
6.已知函数,若f(m)+2f(﹣m)>0,则实数m的取值范围为( )
A.(﹣∞,﹣1)∪(1,+∞) B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣e)∪(0,e) D.(﹣∞,﹣1)∪(0,1)
解:当m>0时则﹣m<0,所以f(m)+2f(﹣m)=lnm﹣2ln(﹣m)>0,
即lnm﹣lnm2=ln>0,解得0<m<1,
当m<0时,﹣m>0,所以f(m)+2f(﹣m)=﹣ln(﹣m)+2lnm>0,
即ln(﹣m)>0,解得m<﹣1,
综上,实数m的取值范围为:(﹣∞,﹣1)∪(0,1),
故选:D.
7.已知函数f(x)=cosx(x∈(0,π))的图象与函数y=tanx的图象交于A,B两点,则△OAB(O为坐标原点)的面积为( )
A. B. C. D.
解:由题意有,有,
有,解得sinx=,或 sinx=﹣(舍去),
由x∈(0,π)可得或,
则点A的坐标为,点B的坐标为,
线段AB中点的坐标为,则△OAB的面积为,
故选:B.
8.已知函数是偶函数,则f(x)在上是减函数的一个θ值是( )
A. B. C. D.
解:函数=2sin(2x+θ+)
∵f(x)是偶函数
∴θ+=,k∈Z
得θ=kπ.
又∵f(x)在上是减函数,
则,
可得:,k∈Z.
当k=0时,
可得.
故选:A.
9.已知、是平面内两个互相垂直的单位向量,若向量满足(﹣)?(﹣)=0,则||的最大值是( )
A.1 B.2 C. D.
解:由题意可得?=0,
可得|+|==,
(﹣)?(﹣)=2+?﹣?(+)
=||2﹣||?|+|cos<(+,>=0,
即为||=cos<+,>,
当cos<+,>=1即+,同向时,
||的最大值是.
故选:C.
10.设函数f(x)=asinx+bcosx,其中a,b∈R,ab≠0,若f(x)≥f()对一切x∈R恒成立,则下列结论中正确的是( )
A.f()=0
B.点(,0)是函数f(x)的一个对称中心
C.f(x)在(0,)上是增函数
D.存在直线经过点(a,b)且与函数f(x)的图象有无数多个交点
解:函数f(x)=asinx+bcosx=sin(x+φ),sinφ,
周期T=2π.
由题意么x=取得最小值,a,b∈R,ab≠0,
∴f()=0不正确;
x=取得最小值,
那么就是相邻的对称中点,
∴点(,0)不是函数f(x)的一个对称中心;
因为x=取得最小值,根据正弦函数的性质可知,f(x)在(0,)是减函数.
故选:D.
11.已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在线段AB上(不包含两个端点),则的取值范围是( )
A. B.[﹣1,1) C. D.[﹣1,0)
解:∵A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在线段AB上(不包含两个端点),
∴,
∴,即,
又∵0<λ<1,∠AOB=120°,
∴点C在线段AB上,且,
∴=,
∵,
∴.
故选:C.
12.已知函数f(x)=的图象上关于y轴对称的点至少有3对,则实数a的取值范围是( )
A. B. C. D.
解:若x>0,则﹣x<0,
∵x<0时,f(x)=sin(x)﹣1,
∴f(﹣x)=sin(﹣x)﹣1=﹣sin(x)﹣1,
则若f(x)=sin(x)﹣1,(x<0)关于y轴对称,
则f(﹣x)=﹣sin(x)﹣1=f(x),
即y=﹣sin(x)﹣1,x>0,
设g(x)=﹣sin(x)﹣1,x>0
作出函数g(x)的图象,
要使y=﹣sin(x)﹣1,x>0与f(x)=logax,x>0的图象至少有3个交点,
则0<a<1且满足g(5)<f(5),
即﹣2<loga5,
即loga5>logaa﹣2,
则5<,
解得0<a<,
故选:D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知函数y=ax﹣3+1(a>0且a≠1)图象恒过定点A在角α的终边上,则tan2α= .
解:∵y=3x﹣3+1恒过点A(3,4),
∴tanα=,
∴tan2==.
故答案为:.
14.如图,在同一个平面内.向量,,的模分别为1,,,与的夹角为α,且,与的夹角为45°.若,则m﹣n= .
解:以O为坐标原点.向量方向为x轴,与向量垂直的方向为y轴,建立平面直角坐标系.
点A的坐标为(1,0),,,
可得点C的坐标为(2,1),,
所以,,
又点B的坐标为(1,3),.,
若,则m+n=2且3n=1,
所以,所以.
故答案为:.
15.△ABC的三个内角为A、B、C,当A为 60 °时,取得最大值,且这个最大值为 .
解:因为A+B+C=180°,则=1﹣2+2cos(﹣)=1﹣2+2sin=﹣2+,
所以当sin=,因为为锐角,所以=30°
即A=60°时,原式的最大值为.
故答案为:60,
16.已知函数(ω>0)在内恰有两个最小值点,则ω的取值范围是 .
解:作出函数(ω>0)的图象,
=,,
要使在内恰有两个最小值点,
所以,解得,即.
故答案为:.
三、解答题(本大题共7小题,共70分)
17.已知tan(π+α)=3,求的值.
解:∵tan(π+α)=tanα=3,
∴原式====7.
18.已知,求的值.
【解答】解∵,,
∴,
∴原式=
=
=
=.
19.已知向量与的夹角为60°,||=3,||=2,=2﹣3,=3+k.
(Ⅰ)若,求实数k的值;
(Ⅱ)是否存在实数k,使得∥?说明理由.
解:(Ⅰ)向量与的夹角为60°,||=3,||=2,=2﹣3,=3+k,
∴?=(2﹣3)?(3+k)=6||2﹣3k||2+(2k﹣9)?||?||?cos60°=54﹣12k+3(2k﹣9)=0,
解得k=;
(Ⅱ)∵∥,
∴存在实数λ可得(2﹣3)=λ(3+k),
∴,解得k=﹣.
20.如图是函数一个周期内的图象,已知点是图象与x轴的交点.点C是图象上的最高点,点C的横坐标为.
(1)求函数f(x)的解析式;
(2)记∠ACB=θ,求tanθ的值.
解:(1)由图可知,函数f(x)的周期为,
∴.
代入点C的坐标,有.
又由,可得,
可得,有,
故函数f(x)的解析式为.
(2)如图.过点C作x轴的垂线,垂足为M.
可得点M的坐标为,
由函数f(x)图象的周期性,可得点B的坐标为,|,,|CM|=1,
在△AMC中,,
在△BMC中,,,
由θ=π﹣(∠CAM+∠CBM).
可得 tanθ=﹣tan(∠CAM+∠CBM)=8,故tanθ=8.
21.如图,G是△OAB的重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线.
(1)设,将用λ、、表示;
(2)设,,证明:是定值.
解:(1)∵,
∴,即=λ()
整理,得=(1﹣λ)+λ
(2)∵G是△OAB的重心,
∴==×(+)=(+)
∵,,=(1﹣λ)+λ
∴=(1﹣λ)+λ
因此,得到,可得,
∴=3(1﹣λ)+3λ=3,即=3(定值).
22.如图(1)所示,用两块宽分别为+1cm和1cm的矩形钢板(|PQ|=+1,|MN|=1),剪裁后在平面内焊成60°的“角型”.
(Ⅰ)设∠POA=x,请问下料时x应取多少度?
(Ⅱ)如图(2)所示,在以O为圆心,OA为半径的扇形钢板区域内雕刻一矩形铭牌DEFG,其中动点F在扇形的弧上,求矩形DEFG面积的最大值.
解:(Ⅰ)过A作AX、AY分别垂直OP、ON于X、Y,则在Rt△OAX与Rt△OAY中,
OA==,
∴=,
∴(+1)sin(60°﹣x)=sinx,
∴sinx=cosx
∴x=45°,
(Ⅱ)由(Ⅰ)知,OF=OA=(+1)×=+,
设∠BOF=θ,EF=OFsinθ=(+)sinθ,
DE=OE﹣OD=OE﹣=(+)cosθ﹣sinθ=(+)(cosθ﹣sinθ),
∴S矩形DEFG=EF?DE=(+)2sinθ(cosθ﹣sinθ)=(+)2[(sin2θ+cos2θ)﹣],
=(+)2[sin(2θ+φ)﹣],
≤(+)2(﹣),
=2+
∴矩形DEFG面积的最大值为2+
23.已知函数.
(1)求函数f(x)的单调区间
(2)将函数f(x)的图象先向左平移个单位,再把图象上各点的横坐标伸长为原来的2倍,得到函数h(x)的图象.若对任意的,不等式成立,求实数p的取值范围.
解:(1)=
==,
由于y=sinθ的单调增区间为,k∈Z,
令,
解得:,
∴f(x)单调增区间为,k∈Z.
(2)由于 ,
向左平移个单位得到 y=的图象,
再将各点横坐标伸长为原来的两倍得:y=的图象,故h(x)=sinx.
不等式,
即 ,即 p?(sinx﹣1)(cosx﹣1)<sin2x,成立.
此时,sinx∈(0,1),cosx∈(0,1),sin2x∈(0,1],
∴(sinx﹣1)(cosx﹣1)>0,sin2x>0,
当p≤0时,不等式恒成立,
当p>0时,,
令=,
∴=,
其中sinx+cosx+sinxcosx+1>0,
∴令F'(x)=0得,sinx=cosx,即,
当时,F'(x)>0,F(x)单调递增,
当时,F'(x)<0,F(x)单调递减,
∴,
∴,即,
综上,.
同课章节目录
