正定县2011—2012学年度第一学期期末教学质量检测八年级数学试卷(附答案)
文档属性
| 名称 | 正定县2011—2012学年度第一学期期末教学质量检测八年级数学试卷(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 106.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-30 15:52:57 | ||
图片预览

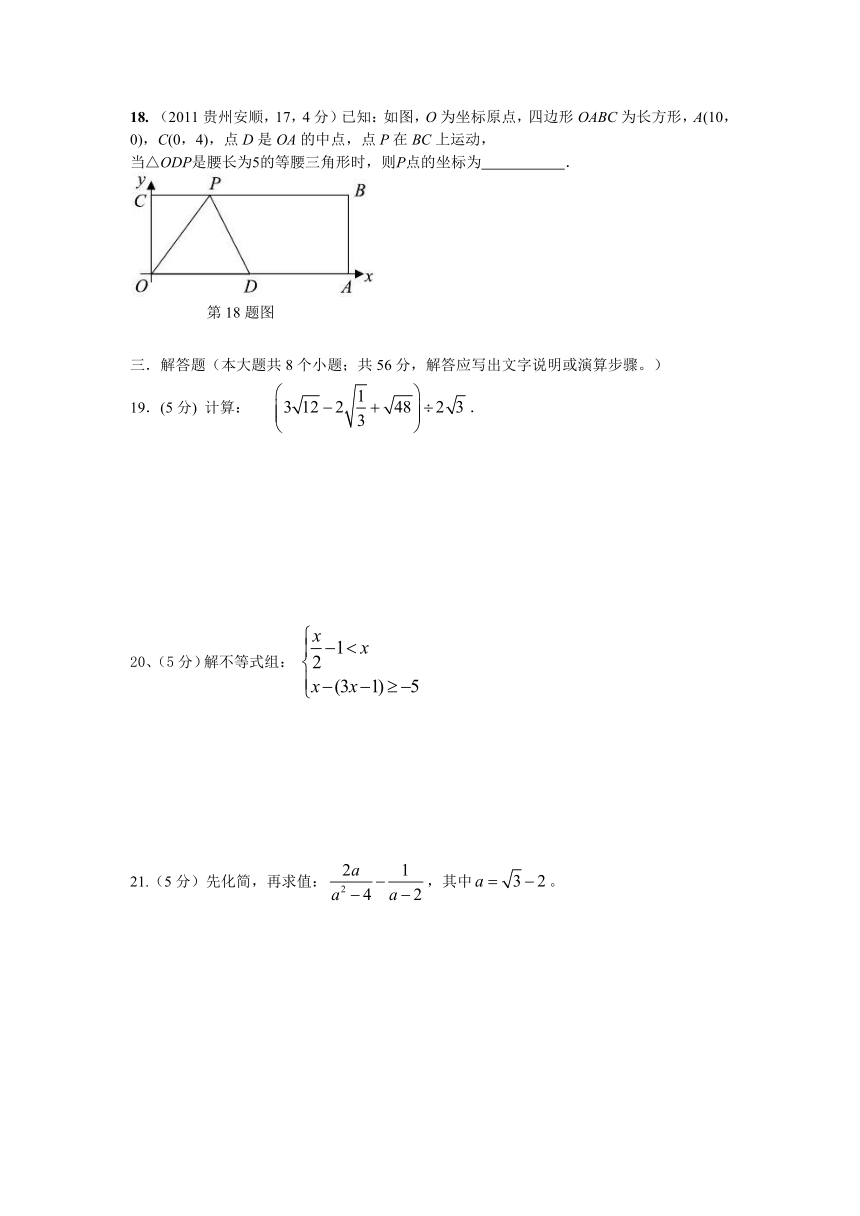
文档简介
正定县2011—2012学年度第一学期期末教学质量检测八年级
(考试时间90分钟,满分100分)
一.选择题(共10个小题,每小题2分,共20分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 四个数-5,0,,中为无理数的是( )
A. -5 B.0 C. D.
2.在平面直角坐标系中,点M(-2,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列事件中,为必然事件的是
A.购买一张彩票,中奖.
B.打开电视,正在播放广告.
C.抛掷一枚硬币,正面向上.
D.一个袋中只装有5个黑球,从中摸出一个球是黑球.
4.下列二次根式中,最简二次根式是( ).
(A) ; (B) ; (C) ; (D) .
5. 点(,1)关于轴对称的点的坐标是( ).
A. (,) B. (2,1) C.(2,) D. (1,)
6. 如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在甲区域内的概率是( )
A.1 B. C. D.
(第9题图)
7.下列计算正确的是( )
A -=2 B.+=
C. D.
8.小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
A、21:10 B、10:21 C、10:51 D、12:01
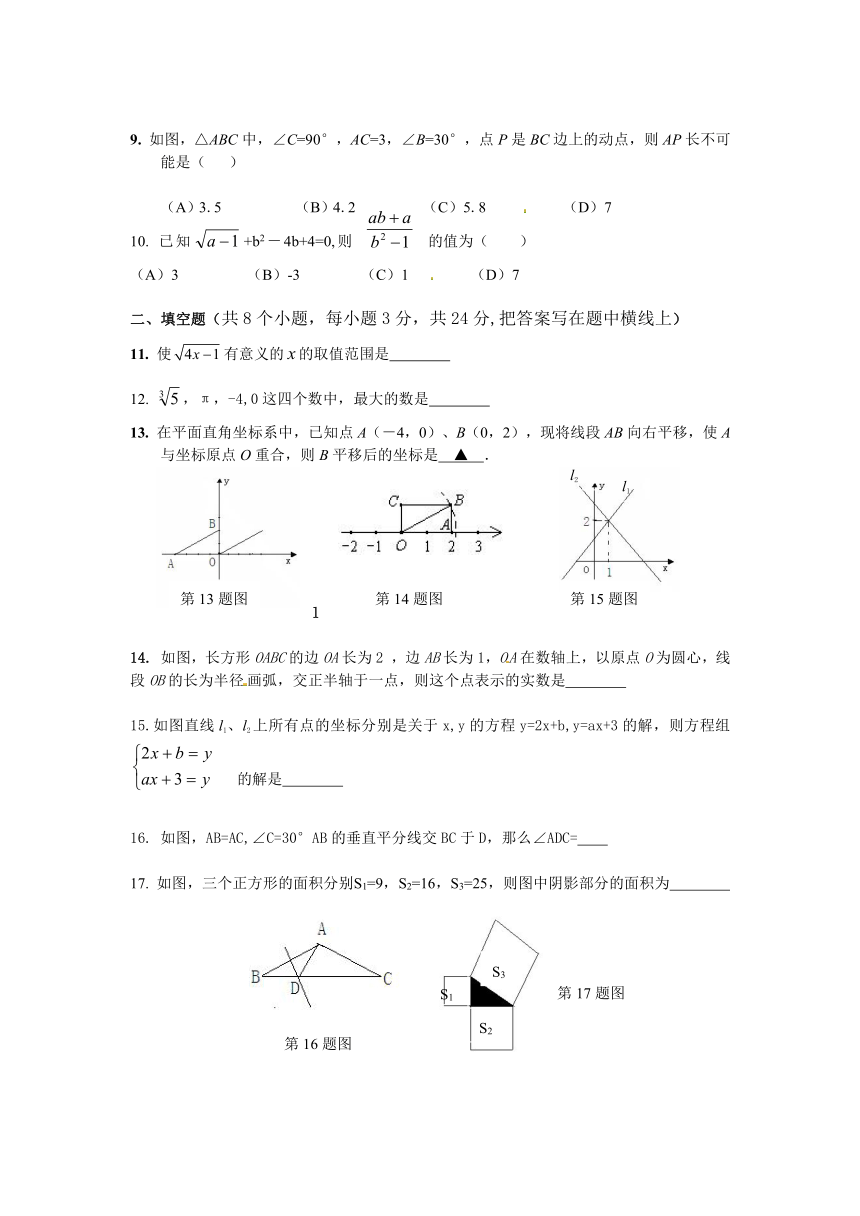
9. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
(A)3.5 (B)4.2 (C)5.8 (D)7
10. 已知+b2-4b+4=0,则 的值为( )
(A)3 (B)-3 (C)1 (D)7
二、填空题(共8个小题,每小题3分,共24分,把答案写在题中横线上)
11. 使有意义的的取值范围是
12. ,π,-4,0这四个数中,最大的数是
13. 在平面直角坐标系中,已知点A(-4,0)、B(0,2),现将线段AB向右平移,使A与坐标原点O重合,则B平移后的坐标是 ▲ .
l
14. 如图,长方形OABC的边OA长为2 ,边AB长为1,OA在数轴上,以原点O为圆心,线段OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是
15.如图直线l1、l2上所有点的坐标分别是关于x,y的方程y=2x+b,y=ax+3的解,则方程组的解是
16. 如图,AB=AC,∠C=30°AB的垂直平分线交BC于D,那么∠ADC=
17. 如图,三个正方形的面积分别S1=9,S2=16,S3=25,则图中阴影部分的面积为
18. (2011贵州安顺,17,4分)已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,
当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
三.解答题(本大题共8个小题;共56分,解答应写出文字说明或演算步骤。)
19.(5分) 计算: .
20、(5分)解不等式组:
21.(5分)先化简,再求值:,其中。
22. (7分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(,5),(,3).
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶点B′的坐标为 .
(4)△ABC的面积为
23. (8分)一只不透明的袋子中装有3个质地、大小均相同的小球,这些小球分别标有数字3、4、x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表:
摸球总次数 10 20 30 60 90 120 180 240 330 450
“和为8”出现的频数 2 10 13 24 30 37 58 82 110 150
“和为8”出现的频率 0.20 0.50 0.43 0.40 0.33 0.31 0.32 0.34 0.33 0.33
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是______;(4分)
(2)若本题中的x=6,求“和为9”的概率(4分)
24.(8分)在甲村至乙村的公路上有一块山地正在开发,现有一C处需要爆破。已知点C处与公路上的两个停靠站A,B的距离分别为300米和400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围250米范围内不得进入,问在进行爆破时,公路AB段是否需要暂时封锁?
25、(8分)某博物馆的门票每张10元,一次购买30张到99张门票按8折优惠,一次购买100张以上(含100张)门票按7折优惠.甲班有56名学生,乙班有54名学生.
(1)若两班学生一起前往该博物馆参观,请问购买门票最少共需花费多少元?
(2)当两班实际前往该博物馆参观的总人数多于30人且不足100人时,至少要有多少人,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜?
26. (10分)已知如图1:△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1) 图1中有几个等腰三角形?EF与BE、CF间有怎样的数量关系.请说明理由。
(2)若AB≠AC,其他条件不变,如图2,图中还有等腰三角形吗?如果有,请分别指出它们.另外第(1)问中EF与BE、CF间的关系还成立吗?
(3) 若△ABC中,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.如图3,这时图中还有哪几个等腰三角形?请直接写出这时EF与BE、CF间的数量关系。
八上期末参考答案
一.DBDCA DCCDC
二.11.X≥;
12.
13.(4,2)
14.
15.
16. 60o
17. 6
18. (2,4) (3,4) (8,4)
三.19.
20 .-2<x≤3
21.
22. ⑴如图…………………………1分
⑵如图…………………………3分
⑶B′(2,1) …………………………5分
(4). 4…………………………7分
23.(1) 0.33 …………………………4分
(2)…………………………8分
24. 解:如图,过C作CD⊥AB于D……………………1分
∵BC=400米,AC=300米,∠ACB=90°,
∴根据勾股定理得AB2= AC2+ BC2=3002+4002=250000,
所以 AB=500米,…………………………4分
由 S△ABC=AB·CD=AC·BC
得 500×CD=300×400
∴CD=240米.…………………………7分
∵240米<250米,故有危险,
因此AB段公路需要暂时封锁.…………………………8分
25. 解:(1)当两个班分别购买门票时,甲班为56×10×0.8=448(元);乙班为54×10×0.8=432(元);所以两班分别购买门票共需花费880元.
当两个班一起购买门票时,甲、乙两班共(56+54)×10×0.7=770(元).
所以两班购买门票最少共需花费770元…………………………3分
(2)当多于30人且不足100人时,设有x人前往参观,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜,根据题意,得,
解这个不等式组,得. …………………………7分
所以,当多于30人且不足100人时,至少有88人前往参观,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜. …………………………8分
26. (1).5个………………………………………………………………1分
EF=BE+CF; ……………………………………………………2分
理由(略)……………………………………………………6分
(2)有,为:△BEO, △CFO;成立…………………………………8分
(3) . △BEO, △CFO;EF=BE-CF…………………………………10分
第8题图
l2
l1
第15题图
第14题图
第13题图
S3
S1
第17题图
S2
第16题图
第18题图
(第19题)
(第22题解答 )
(考试时间90分钟,满分100分)
一.选择题(共10个小题,每小题2分,共20分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 四个数-5,0,,中为无理数的是( )
A. -5 B.0 C. D.
2.在平面直角坐标系中,点M(-2,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列事件中,为必然事件的是
A.购买一张彩票,中奖.
B.打开电视,正在播放广告.
C.抛掷一枚硬币,正面向上.
D.一个袋中只装有5个黑球,从中摸出一个球是黑球.
4.下列二次根式中,最简二次根式是( ).
(A) ; (B) ; (C) ; (D) .
5. 点(,1)关于轴对称的点的坐标是( ).
A. (,) B. (2,1) C.(2,) D. (1,)
6. 如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在甲区域内的概率是( )
A.1 B. C. D.
(第9题图)
7.下列计算正确的是( )
A -=2 B.+=
C. D.
8.小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
A、21:10 B、10:21 C、10:51 D、12:01
9. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
(A)3.5 (B)4.2 (C)5.8 (D)7
10. 已知+b2-4b+4=0,则 的值为( )
(A)3 (B)-3 (C)1 (D)7
二、填空题(共8个小题,每小题3分,共24分,把答案写在题中横线上)
11. 使有意义的的取值范围是
12. ,π,-4,0这四个数中,最大的数是
13. 在平面直角坐标系中,已知点A(-4,0)、B(0,2),现将线段AB向右平移,使A与坐标原点O重合,则B平移后的坐标是 ▲ .
l
14. 如图,长方形OABC的边OA长为2 ,边AB长为1,OA在数轴上,以原点O为圆心,线段OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是
15.如图直线l1、l2上所有点的坐标分别是关于x,y的方程y=2x+b,y=ax+3的解,则方程组的解是
16. 如图,AB=AC,∠C=30°AB的垂直平分线交BC于D,那么∠ADC=
17. 如图,三个正方形的面积分别S1=9,S2=16,S3=25,则图中阴影部分的面积为
18. (2011贵州安顺,17,4分)已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,
当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
三.解答题(本大题共8个小题;共56分,解答应写出文字说明或演算步骤。)
19.(5分) 计算: .
20、(5分)解不等式组:
21.(5分)先化简,再求值:,其中。
22. (7分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(,5),(,3).
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶点B′的坐标为 .
(4)△ABC的面积为
23. (8分)一只不透明的袋子中装有3个质地、大小均相同的小球,这些小球分别标有数字3、4、x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表:
摸球总次数 10 20 30 60 90 120 180 240 330 450
“和为8”出现的频数 2 10 13 24 30 37 58 82 110 150
“和为8”出现的频率 0.20 0.50 0.43 0.40 0.33 0.31 0.32 0.34 0.33 0.33
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是______;(4分)
(2)若本题中的x=6,求“和为9”的概率(4分)
24.(8分)在甲村至乙村的公路上有一块山地正在开发,现有一C处需要爆破。已知点C处与公路上的两个停靠站A,B的距离分别为300米和400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围250米范围内不得进入,问在进行爆破时,公路AB段是否需要暂时封锁?
25、(8分)某博物馆的门票每张10元,一次购买30张到99张门票按8折优惠,一次购买100张以上(含100张)门票按7折优惠.甲班有56名学生,乙班有54名学生.
(1)若两班学生一起前往该博物馆参观,请问购买门票最少共需花费多少元?
(2)当两班实际前往该博物馆参观的总人数多于30人且不足100人时,至少要有多少人,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜?
26. (10分)已知如图1:△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1) 图1中有几个等腰三角形?EF与BE、CF间有怎样的数量关系.请说明理由。
(2)若AB≠AC,其他条件不变,如图2,图中还有等腰三角形吗?如果有,请分别指出它们.另外第(1)问中EF与BE、CF间的关系还成立吗?
(3) 若△ABC中,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.如图3,这时图中还有哪几个等腰三角形?请直接写出这时EF与BE、CF间的数量关系。
八上期末参考答案
一.DBDCA DCCDC
二.11.X≥;
12.
13.(4,2)
14.
15.
16. 60o
17. 6
18. (2,4) (3,4) (8,4)
三.19.
20 .-2<x≤3
21.
22. ⑴如图…………………………1分
⑵如图…………………………3分
⑶B′(2,1) …………………………5分
(4). 4…………………………7分
23.(1) 0.33 …………………………4分
(2)…………………………8分
24. 解:如图,过C作CD⊥AB于D……………………1分
∵BC=400米,AC=300米,∠ACB=90°,
∴根据勾股定理得AB2= AC2+ BC2=3002+4002=250000,
所以 AB=500米,…………………………4分
由 S△ABC=AB·CD=AC·BC
得 500×CD=300×400
∴CD=240米.…………………………7分
∵240米<250米,故有危险,
因此AB段公路需要暂时封锁.…………………………8分
25. 解:(1)当两个班分别购买门票时,甲班为56×10×0.8=448(元);乙班为54×10×0.8=432(元);所以两班分别购买门票共需花费880元.
当两个班一起购买门票时,甲、乙两班共(56+54)×10×0.7=770(元).
所以两班购买门票最少共需花费770元…………………………3分
(2)当多于30人且不足100人时,设有x人前往参观,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜,根据题意,得,
解这个不等式组,得. …………………………7分
所以,当多于30人且不足100人时,至少有88人前往参观,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜. …………………………8分
26. (1).5个………………………………………………………………1分
EF=BE+CF; ……………………………………………………2分
理由(略)……………………………………………………6分
(2)有,为:△BEO, △CFO;成立…………………………………8分
(3) . △BEO, △CFO;EF=BE-CF…………………………………10分
第8题图
l2
l1
第15题图
第14题图
第13题图
S3
S1
第17题图
S2
第16题图
第18题图
(第19题)
(第22题解答 )
同课章节目录
