2020--2021学年 北师大版七年级数学下册6.3 等可能事件的概率(第2课时)课件(24张)
文档属性
| 名称 | 2020--2021学年 北师大版七年级数学下册6.3 等可能事件的概率(第2课时)课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1022.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
6.3
等可能事件的概率
(第2课时)
北师大版
数学
七年级
下册
一个箱子中放有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,那么这个游戏是否公平?
导入新知
1.
进一步理解等可能事件概率的意义.
2.
通过小组合作、交流、试验,初步理解游戏的公平性,会设计简单的公平的游戏.
素养目标
3.
灵活应用概率的计算方法解决各种类型的实际问题.
议一议:
(1)一个袋中装有2个红球和3个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
小明说:“摸出的球不是红球就是白球,所以摸到红球和白球的可能性相同,P(红球)=
”
你觉得小明说得对吗?
不对
知识点
与摸球有关的等可能事件的概率
探究新知
小凡说:“红球有2个,而白球有3个,将每一个球都编上号码,1号球(红色),2号球(红色),3号球(白色),4号球(白色),5号球(白色),摸出每一个球的可能性相同,共有5种等可能的结果.摸到红球可能出现的结果有:摸出1号球或2号球,共有2种等可能的结果,所以,P(摸到红球)=
”
你觉得小凡说得对吗?
对
探究新知
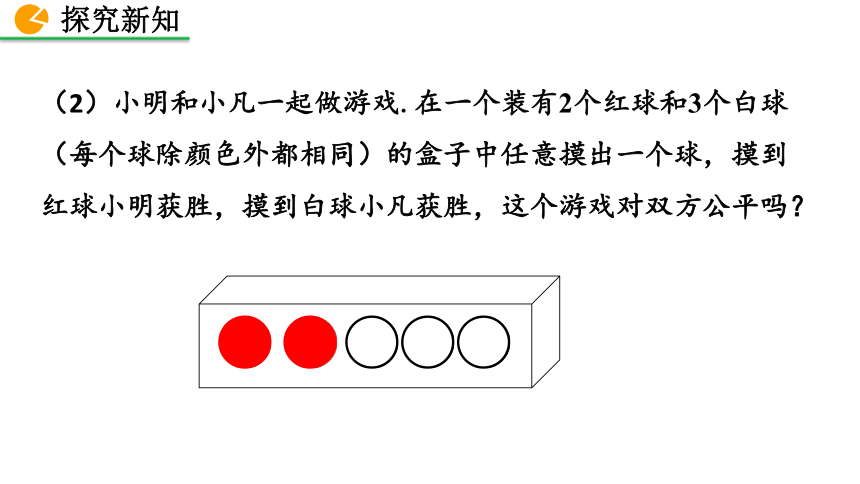
(2)小明和小凡一起做游戏.在一个装有2个红球和3个白球(每个球除颜色外都相同)的盒子中任意摸出一个球,摸到红球小明获胜,摸到白球小凡获胜,这个游戏对双方公平吗?
探究新知
解:
这个游戏不公平.
理由是:如果将每一个球都编上号码,从盒中任意摸出一个球,
摸出红球可能出现两种等可能的结果:
1号球,
2号球,
3号球,
4号球,
5号球,
共有5种等可能的结果:
摸出1号球
或2号球.
P(摸到红球)=
探究新知
1
2
3
4
5
所以这个游戏不公平.
摸出白球可能出现三种等可能的结果:
摸出3号球
或4号球或5号球.
P(摸到白球)=
因为
在一个双人游戏中,你是怎样理解游戏对双方公平的?
双方赢的可能性相等就公平.
探究新知
例1
袋中装有3个球,2红1白,除颜色外,其余如材料、大小、质量等完全相同,随意从中抽取1个球,抽到红球的概率是多少?
故抽得红球这个事件的概率为
解:
抽出的球共有三种等可能的结果:红1,红2,白,
三个结果中有两个结果使得事件A(抽得红球)发生,
P(抽到红球)=
探究新知
素养考点
1
求摸球事件的概率
一个不透明的口袋中有3个红球,2个白球和1个黑球,它们除颜色外完全相同,从中任意摸出一个球,则摸出的是黑球的概率是
.
解析:因为在不透明的布袋中装有3个红球,2个白球,1个黑球,所以从袋中任意摸出一个球,摸出的球是黑球的概率是:
.
巩固练习
变式训练
例2
给你8个除颜色外完全相同的球,请你设计两个摸球游戏,分别满足:
(1)摸到红球的概率是
;
(2)摸到“白球或绿球”的概率是
.
探究新知
素养考点
2
设计摸球游戏的概率事件
解:(1)设袋中只有红球、白球和绿球,其中有x个红球,则有8﹣x个白球和绿球,
所以摸到红球的概率为
,解得x=2.
所以可这样设计:用8粒除颜色外完全相同的红球和白球、绿球设计一个摸球游戏,其中红球有2个.
探究新知
(2)设袋中只有红球、白球和绿球,其中有白球或绿球y个,
所以摸到白球或绿球的概率为
,解得y=5.
所以可这样设计:用8粒除颜色外完全相同的红球和白球、绿球设计一个摸球游戏,其中白球和绿球共有5个.
请你设计一个摸球游戏,要求:
(1)袋子中要有黄球、绿球和红球三种球.
(2)摸到球的概率;P(摸到红球)=
;
P(摸到黄球)=
;并求出摸到绿球的概率有多大?
解:由题意,可设计一个摸球游戏:在一个不透明的袋中,装有12个黄球、绿球和红球,其中红球3个、黄球8个,他们除了颜色外都相同.
因为绿球有12﹣3﹣8=1个,
所以任意从中摸出一个球,则P(摸到绿球)=
.
巩固练习
变式训练
例3
在一个不透明的袋中有6个除颜色外其他都相同的小球,其中3个红球,2个黄球,1个白球.
(1)乐乐从中任意摸出一个小球,摸到的白球机会是多少?
(2)乐乐和亮亮商定一个游戏,规则如下:乐乐从中任意摸出一个小球,摸到红球则乐乐胜,否则亮亮胜,问该游戏对双方是否公平?为什么?
探究新知
素养考点
3
摸球游戏的公平性
解:(1)因为在一个不透明的口袋中有6个除颜色外其余都相同的小球,其中3个红球,2个黄球,1个白球,
所以P(摸出一个白球)=
(2)该游戏对双方是公平的.理由如下:由题意可知P(乐乐获胜)=
P(亮亮获胜)=
所以他们获胜的概率相等,即游戏是公平的.
方法总结:判断游戏是否公平,关键是看双方在游戏中所关注的事件所发生的概率是否相同.
探究新知
规定:在一副去掉大、小王的扑克牌中,牌面从小到大的顺序为:2、3、4、5、6、7、8、9、10、J、Q、K、A,且牌面的大小与花色无关.
小明和小颖做摸牌游戏,他们先后从这副去掉大、小王的扑克牌中任意抽取一张牌(不放回),谁摸到的牌面大,谁就获胜.现小明已经摸到的牌面为4,然后小颖摸牌,
P(小明获胜)=
.
8
51
P(小颖获胜)=
.
40
51
巩固练习
变式训练
(2020?绥化)在一个不透明的袋子中装有黑球m个、白球n
个、红球3个,除颜色外无其它差别,任意摸出一个球是红
球的概率是( )
A.
B.
C.
D.
连接中考
B
1.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是(
)
A.
B.
C.
D.
2.小玲在一次班会中参与知识抢答活动,现有语文题6道,数学题5道,综合题9道,她从中随机抽取1道,抽中数学题的概率是(
)
A.
B.
C.
D.
C
C
课堂检测
基础巩固题
3.用6个球(除颜色外没有区别)设计满足以下条件的游戏:摸到白球、红球、黄球的概率分别为
则应准备的白球、红球、黄球的个数分别为(
)
A.3,2,1
B.1,2,3
C.3,1,2
D.2,3,1
4.布袋中装有3个红球和6个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是
.
A
课堂检测
基础巩固题
5.在一个不透明的袋中装有2个黄球,3个黑球和5个红球,它们除颜色外其他都相同.将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;
解:因为共10个球,有2个黄球,
所以P(黄球)=
.
课堂检测
基础巩固题
任意抛掷一枚均匀的骰子,当骰子停止转动后,朝上一面的数是奇数的概率是多少?是正数的概率是多少?是负数的概率是多少?
是正数的有6种可能,即1,2,3,4,5,6,所以朝上一面的数是
正数的概率
;
是负数的有0种可能,即所有可能的结果都不是负数,所
以朝上一面的数是负数的概率
.
解:任意抛掷一枚均匀的骰子,当它停止运动后,朝上一面的数有可能性相同的6种可能,即1,2,3,4,5,6.是奇数的有3种可能,即1,3,5,所以朝上一面的数是奇数的概率
课堂检测
能力提升题
已知一纸箱中装有5个只有颜色不同的球,其中2个白球,3个红球.
(1)求从箱中随机取出一个球是白球的概率是多少?
(2)如果随机取出一个球是白球的概率为
,则应往纸箱内加放几个红球?
解:
(1)P(白球)=
;
(2)设应加x个红球,则
解得x=7.
所以应往纸箱内加放7个红球.
课堂检测
拓广探索题
1.计算常见事件发生的概率.
2.游戏公平的原则.
3.根据题目要求设计符合条件的游戏.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
6.3
等可能事件的概率
(第2课时)
北师大版
数学
七年级
下册
一个箱子中放有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,那么这个游戏是否公平?
导入新知
1.
进一步理解等可能事件概率的意义.
2.
通过小组合作、交流、试验,初步理解游戏的公平性,会设计简单的公平的游戏.
素养目标
3.
灵活应用概率的计算方法解决各种类型的实际问题.
议一议:
(1)一个袋中装有2个红球和3个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
小明说:“摸出的球不是红球就是白球,所以摸到红球和白球的可能性相同,P(红球)=
”
你觉得小明说得对吗?
不对
知识点
与摸球有关的等可能事件的概率
探究新知
小凡说:“红球有2个,而白球有3个,将每一个球都编上号码,1号球(红色),2号球(红色),3号球(白色),4号球(白色),5号球(白色),摸出每一个球的可能性相同,共有5种等可能的结果.摸到红球可能出现的结果有:摸出1号球或2号球,共有2种等可能的结果,所以,P(摸到红球)=
”
你觉得小凡说得对吗?
对
探究新知
(2)小明和小凡一起做游戏.在一个装有2个红球和3个白球(每个球除颜色外都相同)的盒子中任意摸出一个球,摸到红球小明获胜,摸到白球小凡获胜,这个游戏对双方公平吗?
探究新知
解:
这个游戏不公平.
理由是:如果将每一个球都编上号码,从盒中任意摸出一个球,
摸出红球可能出现两种等可能的结果:
1号球,
2号球,
3号球,
4号球,
5号球,
共有5种等可能的结果:
摸出1号球
或2号球.
P(摸到红球)=
探究新知
1
2
3
4
5
所以这个游戏不公平.
摸出白球可能出现三种等可能的结果:
摸出3号球
或4号球或5号球.
P(摸到白球)=
因为
在一个双人游戏中,你是怎样理解游戏对双方公平的?
双方赢的可能性相等就公平.
探究新知
例1
袋中装有3个球,2红1白,除颜色外,其余如材料、大小、质量等完全相同,随意从中抽取1个球,抽到红球的概率是多少?
故抽得红球这个事件的概率为
解:
抽出的球共有三种等可能的结果:红1,红2,白,
三个结果中有两个结果使得事件A(抽得红球)发生,
P(抽到红球)=
探究新知
素养考点
1
求摸球事件的概率
一个不透明的口袋中有3个红球,2个白球和1个黑球,它们除颜色外完全相同,从中任意摸出一个球,则摸出的是黑球的概率是
.
解析:因为在不透明的布袋中装有3个红球,2个白球,1个黑球,所以从袋中任意摸出一个球,摸出的球是黑球的概率是:
.
巩固练习
变式训练
例2
给你8个除颜色外完全相同的球,请你设计两个摸球游戏,分别满足:
(1)摸到红球的概率是
;
(2)摸到“白球或绿球”的概率是
.
探究新知
素养考点
2
设计摸球游戏的概率事件
解:(1)设袋中只有红球、白球和绿球,其中有x个红球,则有8﹣x个白球和绿球,
所以摸到红球的概率为
,解得x=2.
所以可这样设计:用8粒除颜色外完全相同的红球和白球、绿球设计一个摸球游戏,其中红球有2个.
探究新知
(2)设袋中只有红球、白球和绿球,其中有白球或绿球y个,
所以摸到白球或绿球的概率为
,解得y=5.
所以可这样设计:用8粒除颜色外完全相同的红球和白球、绿球设计一个摸球游戏,其中白球和绿球共有5个.
请你设计一个摸球游戏,要求:
(1)袋子中要有黄球、绿球和红球三种球.
(2)摸到球的概率;P(摸到红球)=
;
P(摸到黄球)=
;并求出摸到绿球的概率有多大?
解:由题意,可设计一个摸球游戏:在一个不透明的袋中,装有12个黄球、绿球和红球,其中红球3个、黄球8个,他们除了颜色外都相同.
因为绿球有12﹣3﹣8=1个,
所以任意从中摸出一个球,则P(摸到绿球)=
.
巩固练习
变式训练
例3
在一个不透明的袋中有6个除颜色外其他都相同的小球,其中3个红球,2个黄球,1个白球.
(1)乐乐从中任意摸出一个小球,摸到的白球机会是多少?
(2)乐乐和亮亮商定一个游戏,规则如下:乐乐从中任意摸出一个小球,摸到红球则乐乐胜,否则亮亮胜,问该游戏对双方是否公平?为什么?
探究新知
素养考点
3
摸球游戏的公平性
解:(1)因为在一个不透明的口袋中有6个除颜色外其余都相同的小球,其中3个红球,2个黄球,1个白球,
所以P(摸出一个白球)=
(2)该游戏对双方是公平的.理由如下:由题意可知P(乐乐获胜)=
P(亮亮获胜)=
所以他们获胜的概率相等,即游戏是公平的.
方法总结:判断游戏是否公平,关键是看双方在游戏中所关注的事件所发生的概率是否相同.
探究新知
规定:在一副去掉大、小王的扑克牌中,牌面从小到大的顺序为:2、3、4、5、6、7、8、9、10、J、Q、K、A,且牌面的大小与花色无关.
小明和小颖做摸牌游戏,他们先后从这副去掉大、小王的扑克牌中任意抽取一张牌(不放回),谁摸到的牌面大,谁就获胜.现小明已经摸到的牌面为4,然后小颖摸牌,
P(小明获胜)=
.
8
51
P(小颖获胜)=
.
40
51
巩固练习
变式训练
(2020?绥化)在一个不透明的袋子中装有黑球m个、白球n
个、红球3个,除颜色外无其它差别,任意摸出一个球是红
球的概率是( )
A.
B.
C.
D.
连接中考
B
1.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是(
)
A.
B.
C.
D.
2.小玲在一次班会中参与知识抢答活动,现有语文题6道,数学题5道,综合题9道,她从中随机抽取1道,抽中数学题的概率是(
)
A.
B.
C.
D.
C
C
课堂检测
基础巩固题
3.用6个球(除颜色外没有区别)设计满足以下条件的游戏:摸到白球、红球、黄球的概率分别为
则应准备的白球、红球、黄球的个数分别为(
)
A.3,2,1
B.1,2,3
C.3,1,2
D.2,3,1
4.布袋中装有3个红球和6个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是
.
A
课堂检测
基础巩固题
5.在一个不透明的袋中装有2个黄球,3个黑球和5个红球,它们除颜色外其他都相同.将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;
解:因为共10个球,有2个黄球,
所以P(黄球)=
.
课堂检测
基础巩固题
任意抛掷一枚均匀的骰子,当骰子停止转动后,朝上一面的数是奇数的概率是多少?是正数的概率是多少?是负数的概率是多少?
是正数的有6种可能,即1,2,3,4,5,6,所以朝上一面的数是
正数的概率
;
是负数的有0种可能,即所有可能的结果都不是负数,所
以朝上一面的数是负数的概率
.
解:任意抛掷一枚均匀的骰子,当它停止运动后,朝上一面的数有可能性相同的6种可能,即1,2,3,4,5,6.是奇数的有3种可能,即1,3,5,所以朝上一面的数是奇数的概率
课堂检测
能力提升题
已知一纸箱中装有5个只有颜色不同的球,其中2个白球,3个红球.
(1)求从箱中随机取出一个球是白球的概率是多少?
(2)如果随机取出一个球是白球的概率为
,则应往纸箱内加放几个红球?
解:
(1)P(白球)=
;
(2)设应加x个红球,则
解得x=7.
所以应往纸箱内加放7个红球.
课堂检测
拓广探索题
1.计算常见事件发生的概率.
2.游戏公平的原则.
3.根据题目要求设计符合条件的游戏.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
