3.2 用关系式表示的变量间关系课件(共24张PPT)
文档属性
| 名称 | 3.2 用关系式表示的变量间关系课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 14:30:07 | ||
图片预览




文档简介
第2节 用关系式表示的变量间关系
第三章 变量之间的关系
2021年春北师大版七年级数学下册
1 根据具体情境,会用关系式表示某些变量之间的关系. (重点)
2 能根据关系式和自变量的值,求出对应的因变量的值.(难点)
学习目标
在“小车下滑的时间”中:
支撑物的高度h和小车下滑的时间t都在变化,它们都是________
其中小车下滑的时间t随支撑物的高度h的变化而变化。
支撑物的高度h是_______
小车下滑的时间t是_______
变量
自变量
因变量
新课导入
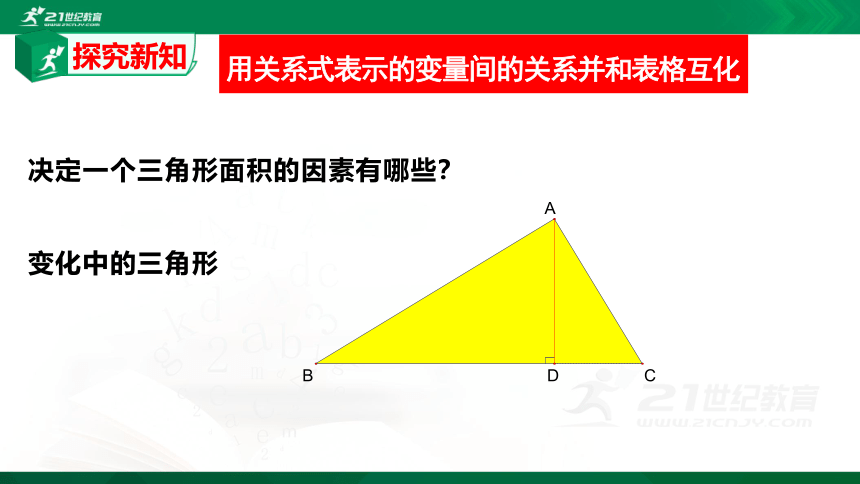
用关系式表示的变量间的关系并和表格互化
决定一个三角形面积的因素有哪些?
变化中的三角形
探究新知
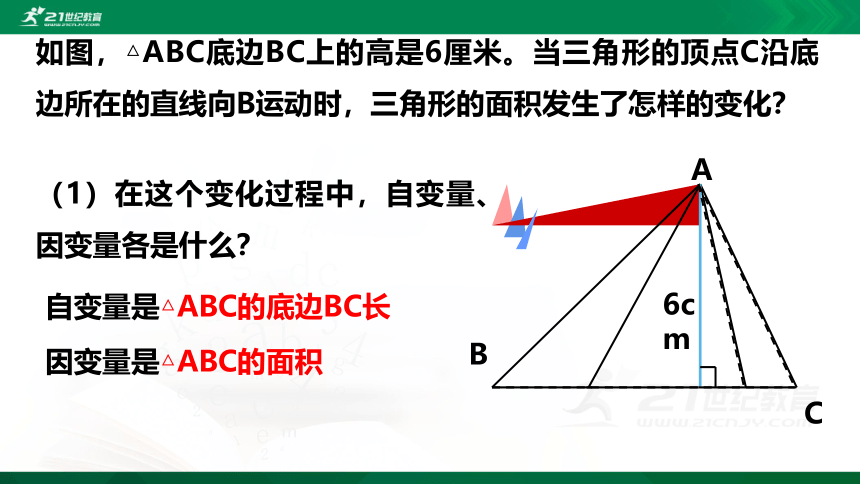
因变量是△ABC的面积
(1)在这个变化过程中,自变量、因变量各是什么?
A
B
C
自变量是△ABC的底边BC长
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
6cm
(2)如果三角形底边BC长为(cm),那么三角形的面积y(cm2)可以表示为 .
y=3x
A
B
C
C
C
C
6cm
(3)当底边长从12厘米变化到3厘米时,三角形的面积从______厘米2变化到_____厘米2
36
9
解: 在y=3x中
当X=12时
y =3×12=36
当X=3时
y=3×3=9
X是底边BC的长,y是⊿ABC的面积
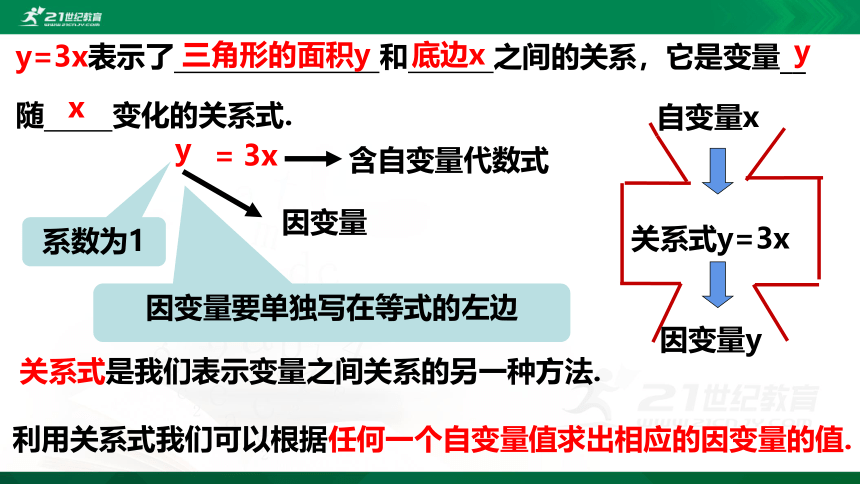
y=3x表示了 和 之间的关系,它是变量__
随 变化的关系式.
三角形的面积y
底边x
3x
含自变量代数式
因变量
系数为1
y
x
=
y
因变量要单独写在等式的左边
自变量x
关系式y=3x
因变量y
关系式是我们表示变量之间关系的另一种方法.
利用关系式我们可以根据任何一个自变量值求出相应的因变量的值.
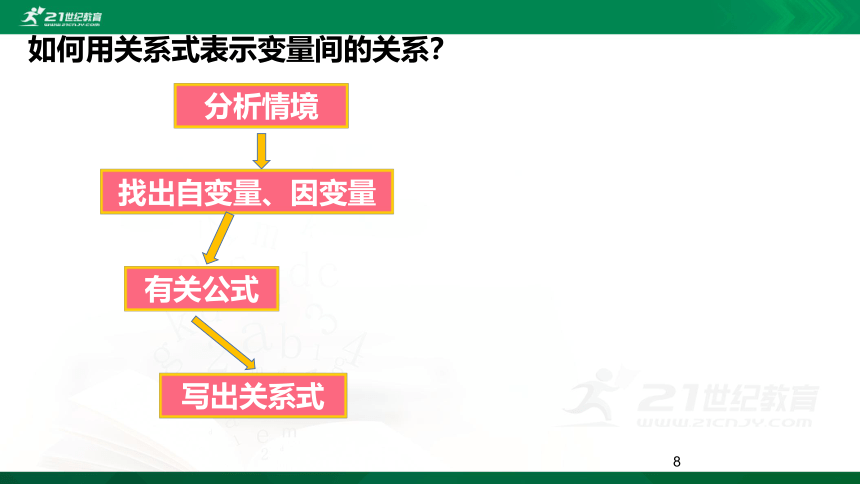
如何用关系式表示变量间的关系?
分析情境
找出自变量、因变量
有关公式
写出关系式
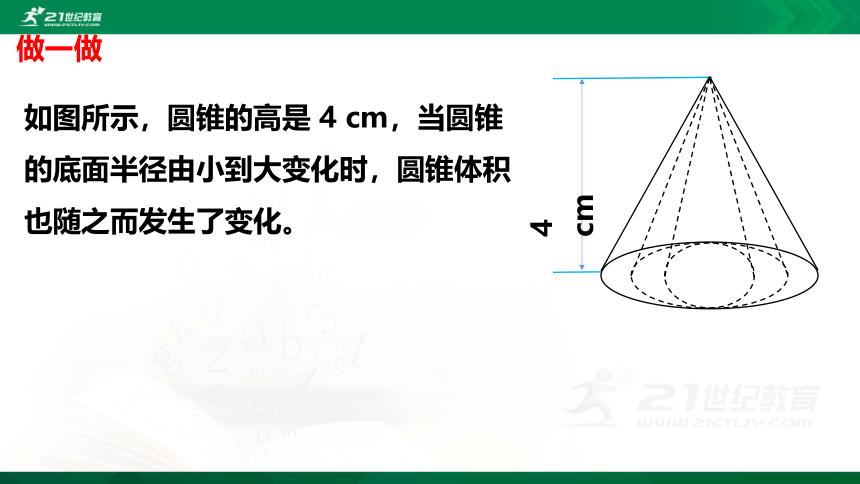
如图所示,圆锥的高是 4 cm,当圆锥的底面半径由小到大变化时,圆锥体积也随之而发生了变化。
4 cm
做一做
4 cm
(1)在这个变化过程中,自变量是_______________
因变量是_______________.
圆锥的底面半径
圆锥的体积
(2)如果圆锥底面半径为 r(cm),那么圆锥的体积V(cm3)与 r 的关系式是____________.
4 cm
(3)当底面半径由 1 cm 变化到 10cm 时,圆锥的体积由 ______ cm3 变化到______cm3.
例1
长方形的周长为24 cm,其中一边长为x cm(x>0),面积为y cm2,则该长方形中y与x的关系可以写为( )
A.y=x2 B.y=(12-x)2
C.y=(12-x)·x D.y=2(12-x)
C
解析:因为长方形的周长为24 cm,其中一边长为x cm,所以另一边长为(12-x) cm,因为面积为y cm2,所以该长方形中y与x的关系可以写为y=(12-x)·x.
例题讲解
用关系式求值
议一议
你知道什么是“低碳生活”吗? “低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.
探究新知
(1)用字母表示家居用电的二氧化碳排放量的公式_____________,其中的字母表示 .
y = 0.785x
耗电量(x)和二氧化碳排放量(y)
(2)在上述关系式中,耗电量每增加 1 kW·h,二氧化碳排放量增加_________.当耗电量从 1 kW·h 增加到100 kW·h 时,二氧化碳排放量从________ 增加到____________.
0.785 kg
0.785 kg
78.5 kg
y = 0.785x
耗电量(x)和二氧化碳排放量(y)
0.785 kg
0.785 kg
78.5 kg
(3)小明家本月用电大约110 kW·h、天然气20m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量。
例2
某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)5年后的年产值是______万元.
解析:(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x年后增加2x万元,所以年产值y(万元)与年数x之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
y=2x+15
25
例题讲解
1 某地海拔高度h与温度T的关系可用T=21-6h来表示(其中温度单位为℃,海拔高度单位为km),则该地区某海拔高度为2 000 m的山顶上的温度为( )
A.15 ℃ B.9 ℃ C.3 ℃ D.7 ℃
课堂练习
2 油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了 .如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的关系式和自变量取值范围分别是( )
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤x≤500
D.y=60-0.12x,0≤x≤500
3 百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x与售价y如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}长度x/m
1
2
3
4
…
售价y/元
8+0.3
16+0.6
24+0.9
32+1.2
…
下列用长度x表示售价y的关系式中,正确的是( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
4 一个长方体的体积为12 cm3,当底面积不变,高增大时,长方体的体积发生变化,若底面积不变,高变为原来的3倍,则体积变为( )
A.12 cm3 B.24 cm3
C.36 cm3 D.48 cm3
1 y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
2 通过表格可表示两个变量之间的关系,本节中利用_______也可表示两个变量之间的关系.
3 确定关系式的步骤:先找出题目中关于________与_______的相等关系,再用_________的代数式表示________
x y
关系式
自变量
因变量
含自变量
因变量
课堂小结
①写关系式时将表示 的字母单独写在等号的左边,含有自变量的代数式放在等式的右边。
②利用关系式可以根据任何一个 的值求出相应的 的值。
因变量
自变量
因变量
谢谢聆听
https://www.21cnjy.com/help/help_extract.php
第三章 变量之间的关系
2021年春北师大版七年级数学下册
1 根据具体情境,会用关系式表示某些变量之间的关系. (重点)
2 能根据关系式和自变量的值,求出对应的因变量的值.(难点)
学习目标
在“小车下滑的时间”中:
支撑物的高度h和小车下滑的时间t都在变化,它们都是________
其中小车下滑的时间t随支撑物的高度h的变化而变化。
支撑物的高度h是_______
小车下滑的时间t是_______
变量
自变量
因变量
新课导入
用关系式表示的变量间的关系并和表格互化
决定一个三角形面积的因素有哪些?
变化中的三角形
探究新知
因变量是△ABC的面积
(1)在这个变化过程中,自变量、因变量各是什么?
A
B
C
自变量是△ABC的底边BC长
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
6cm
(2)如果三角形底边BC长为(cm),那么三角形的面积y(cm2)可以表示为 .
y=3x
A
B
C
C
C
C
6cm
(3)当底边长从12厘米变化到3厘米时,三角形的面积从______厘米2变化到_____厘米2
36
9
解: 在y=3x中
当X=12时
y =3×12=36
当X=3时
y=3×3=9
X是底边BC的长,y是⊿ABC的面积
y=3x表示了 和 之间的关系,它是变量__
随 变化的关系式.
三角形的面积y
底边x
3x
含自变量代数式
因变量
系数为1
y
x
=
y
因变量要单独写在等式的左边
自变量x
关系式y=3x
因变量y
关系式是我们表示变量之间关系的另一种方法.
利用关系式我们可以根据任何一个自变量值求出相应的因变量的值.
如何用关系式表示变量间的关系?
分析情境
找出自变量、因变量
有关公式
写出关系式
如图所示,圆锥的高是 4 cm,当圆锥的底面半径由小到大变化时,圆锥体积也随之而发生了变化。
4 cm
做一做
4 cm
(1)在这个变化过程中,自变量是_______________
因变量是_______________.
圆锥的底面半径
圆锥的体积
(2)如果圆锥底面半径为 r(cm),那么圆锥的体积V(cm3)与 r 的关系式是____________.
4 cm
(3)当底面半径由 1 cm 变化到 10cm 时,圆锥的体积由 ______ cm3 变化到______cm3.
例1
长方形的周长为24 cm,其中一边长为x cm(x>0),面积为y cm2,则该长方形中y与x的关系可以写为( )
A.y=x2 B.y=(12-x)2
C.y=(12-x)·x D.y=2(12-x)
C
解析:因为长方形的周长为24 cm,其中一边长为x cm,所以另一边长为(12-x) cm,因为面积为y cm2,所以该长方形中y与x的关系可以写为y=(12-x)·x.
例题讲解
用关系式求值
议一议
你知道什么是“低碳生活”吗? “低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.
探究新知
(1)用字母表示家居用电的二氧化碳排放量的公式_____________,其中的字母表示 .
y = 0.785x
耗电量(x)和二氧化碳排放量(y)
(2)在上述关系式中,耗电量每增加 1 kW·h,二氧化碳排放量增加_________.当耗电量从 1 kW·h 增加到100 kW·h 时,二氧化碳排放量从________ 增加到____________.
0.785 kg
0.785 kg
78.5 kg
y = 0.785x
耗电量(x)和二氧化碳排放量(y)
0.785 kg
0.785 kg
78.5 kg
(3)小明家本月用电大约110 kW·h、天然气20m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量。
例2
某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)5年后的年产值是______万元.
解析:(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x年后增加2x万元,所以年产值y(万元)与年数x之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
y=2x+15
25
例题讲解
1 某地海拔高度h与温度T的关系可用T=21-6h来表示(其中温度单位为℃,海拔高度单位为km),则该地区某海拔高度为2 000 m的山顶上的温度为( )
A.15 ℃ B.9 ℃ C.3 ℃ D.7 ℃
课堂练习
2 油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了 .如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的关系式和自变量取值范围分别是( )
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤x≤500
D.y=60-0.12x,0≤x≤500
3 百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x与售价y如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}长度x/m
1
2
3
4
…
售价y/元
8+0.3
16+0.6
24+0.9
32+1.2
…
下列用长度x表示售价y的关系式中,正确的是( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
4 一个长方体的体积为12 cm3,当底面积不变,高增大时,长方体的体积发生变化,若底面积不变,高变为原来的3倍,则体积变为( )
A.12 cm3 B.24 cm3
C.36 cm3 D.48 cm3
1 y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
2 通过表格可表示两个变量之间的关系,本节中利用_______也可表示两个变量之间的关系.
3 确定关系式的步骤:先找出题目中关于________与_______的相等关系,再用_________的代数式表示________
x y
关系式
自变量
因变量
含自变量
因变量
课堂小结
①写关系式时将表示 的字母单独写在等号的左边,含有自变量的代数式放在等式的右边。
②利用关系式可以根据任何一个 的值求出相应的 的值。
因变量
自变量
因变量
谢谢聆听
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
