2020-2021学年八年级数学人教版下册第十八章平行四边形的性质与判定判定靶向专题提升练习(word版无答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第十八章平行四边形的性质与判定判定靶向专题提升练习(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 269.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 14:55:45 | ||
图片预览


文档简介
人教版八年级下册数学《平行四边形的性质与判定》
靶向专题提升练习
一.选择题.
1.
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为( )
A.54°
B.36°
C.46°
D.126°
2.
如图,△ABC中,AE=DF,AF=DE,AB=AC=15,那么四边形AFDE的周长是( )
A.30
B.25
C.20
D.15
3.
如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,
BE=ED=3,AC=10,则四边形ABCD的面积为( )
A.6
B.12
C.20
D.24
4.
已知一个四边形的四边依次是a,b,c,d,且满足2a2+b2+2c2+d2=4ac+2bd,则这个四边形的形状是(
)
A.任意四边形
B.对角线互相垂直的四边形
C.平行四边形
D.对角线相等的四边形
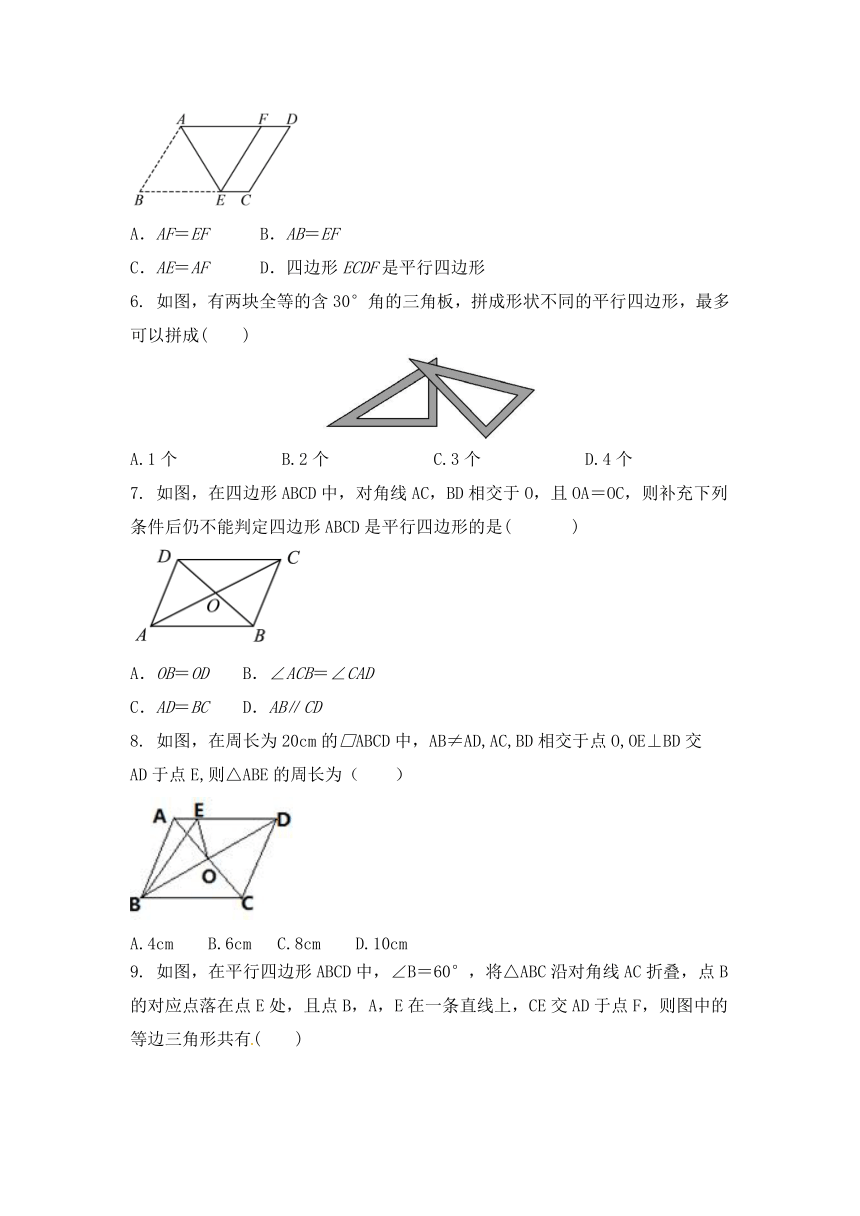
5.
如图,将?ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是(
)
A.AF=EF
B.AB=EF
C.AE=AF
D.四边形ECDF是平行四边形
6.
如图,有两块全等的含30°角的三角板,拼成形状不同的平行四边形,最多可以拼成( )
A.1个
B.2个
C.3个
D.4个
7.
如图,在四边形ABCD中,对角线AC,BD相交于O,且OA=OC,则补充下列条件后仍不能判定四边形ABCD是平行四边形的是(
)
A.OB=OD
B.∠ACB=∠CAD
C.AD=BC
D.AB∥CD
8.
如图,在周长为20cm的□ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交
AD于点E,则△ABE的周长为(
)
A.4cm
B.6cm
C.8cm
D.10cm
9.
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中的等边三角形共有( )
A.4个
B.3个
C.2个
D.1个
10.
四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;
②如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;
③如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①
B.①②③
C.②
D.②③
二.填空题.
11.
小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的数学依据是_____________________________________.
12.
如图,AD是△ABC的边BC上的中线,延长AD到点E,使DE=AD,连接BE,CE,则四边形ABEC是_______四边形.
13.
如图,ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是____.
14.
如图,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,AB∶CD=1∶2,
若△ABC的面积为6,则△BCD的面积为
.?
15.
如图,平行四边形
ABCD的周长为20,BE⊥AD,BF⊥CD,BE=2,BF=3.则平行四边形
ABCD的面积为
.
16.
如图,在□ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=
度.?
17.
如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为F,与DC的延长线相交于点H,则△DEF的面积是____.
18.
如图,在四边形ABCD中,AD∥BC,且AD>BC,AD=8
cm,BC=6
cm,P,Q分别从A,C同时出发,P以1
cm/s的速度由A向D运动,Q以2
cm/s的速度由C出发向B运动,____秒后,四边形ABQP是平行四边形.
三.解答题.
19.
如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED∥BC,EF∥AC.求证:BE=CF.
20.
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
21.
如图,F,C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE,BD.求证:四边形ABDE是平行四边形.
22.
如图,在?ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
23.
如图,BD是ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AF=CE.
24.
如图,将□ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
25.
如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。
靶向专题提升练习
一.选择题.
1.
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为( )
A.54°
B.36°
C.46°
D.126°
2.
如图,△ABC中,AE=DF,AF=DE,AB=AC=15,那么四边形AFDE的周长是( )
A.30
B.25
C.20
D.15
3.
如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,
BE=ED=3,AC=10,则四边形ABCD的面积为( )
A.6
B.12
C.20
D.24
4.
已知一个四边形的四边依次是a,b,c,d,且满足2a2+b2+2c2+d2=4ac+2bd,则这个四边形的形状是(
)
A.任意四边形
B.对角线互相垂直的四边形
C.平行四边形
D.对角线相等的四边形
5.
如图,将?ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是(
)
A.AF=EF
B.AB=EF
C.AE=AF
D.四边形ECDF是平行四边形
6.
如图,有两块全等的含30°角的三角板,拼成形状不同的平行四边形,最多可以拼成( )
A.1个
B.2个
C.3个
D.4个
7.
如图,在四边形ABCD中,对角线AC,BD相交于O,且OA=OC,则补充下列条件后仍不能判定四边形ABCD是平行四边形的是(
)
A.OB=OD
B.∠ACB=∠CAD
C.AD=BC
D.AB∥CD
8.
如图,在周长为20cm的□ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交
AD于点E,则△ABE的周长为(
)
A.4cm
B.6cm
C.8cm
D.10cm
9.
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中的等边三角形共有( )
A.4个
B.3个
C.2个
D.1个
10.
四边形ABCD,AC与BD相交于点O,如果给出条件AB∥CD,那么还不能判定四边形ABCD为平行四边形,以下说法正确的是( )
①如果再加上条件BC=AD,那么四边形ABCD一定是平行四边形;
②如果再加上条件AO=CO,那么四边形ABCD一定是平行四边形;
③如果再加上条件∠DBA=∠CAB,那么四边形ABCD一定是平行四边形.
A.①
B.①②③
C.②
D.②③
二.填空题.
11.
小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的数学依据是_____________________________________.
12.
如图,AD是△ABC的边BC上的中线,延长AD到点E,使DE=AD,连接BE,CE,则四边形ABEC是_______四边形.
13.
如图,ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是____.
14.
如图,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,AB∶CD=1∶2,
若△ABC的面积为6,则△BCD的面积为
.?
15.
如图,平行四边形
ABCD的周长为20,BE⊥AD,BF⊥CD,BE=2,BF=3.则平行四边形
ABCD的面积为
.
16.
如图,在□ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=
度.?
17.
如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为F,与DC的延长线相交于点H,则△DEF的面积是____.
18.
如图,在四边形ABCD中,AD∥BC,且AD>BC,AD=8
cm,BC=6
cm,P,Q分别从A,C同时出发,P以1
cm/s的速度由A向D运动,Q以2
cm/s的速度由C出发向B运动,____秒后,四边形ABQP是平行四边形.
三.解答题.
19.
如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED∥BC,EF∥AC.求证:BE=CF.
20.
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
21.
如图,F,C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE,BD.求证:四边形ABDE是平行四边形.
22.
如图,在?ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
23.
如图,BD是ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AF=CE.
24.
如图,将□ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
25.
如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。
