2020-2021学年八年级数学人教版下册 18.2. 2.1 菱形的性质课件(共33张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 18.2. 2.1 菱形的性质课件(共33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
18.2.2.1
菱形的性质
学习目标
1
2
3
理解菱形的概念,会用菱形的性质解决简单的问题
体会几何图形研究的一般步骤和方法
通过探究和应用的过程提高几何直观能力和推理能力
学习重难点
重点
难点
菱形的性质及应用
菱形性质的探索及面积公式的推导
提出问题
引发思考
生活中美丽的菱形图案
菱形是特殊的平行四边形
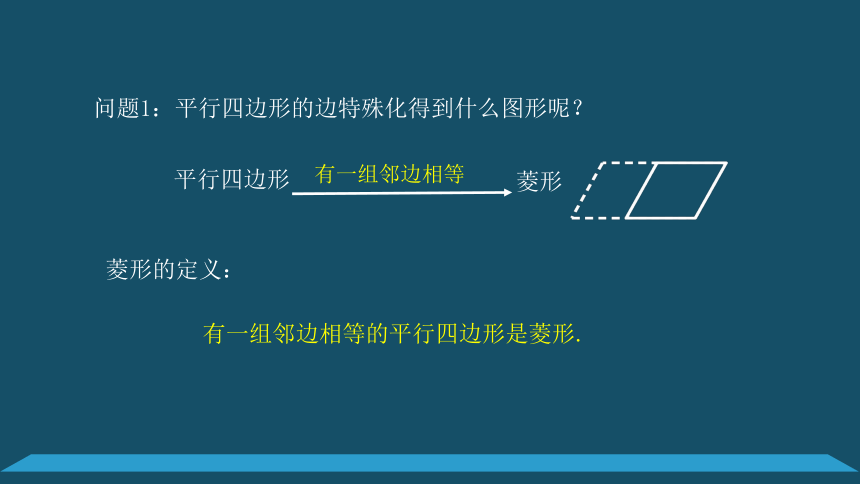
平行四边形
菱形
有一组邻边相等
菱形的定义:
有一组邻边相等的平行四边形是菱形.
问题1:平行四边形的边特殊化得到什么图形呢?
问题2:菱形作为特殊的平行四边形,具有平行四边形的所有性质.
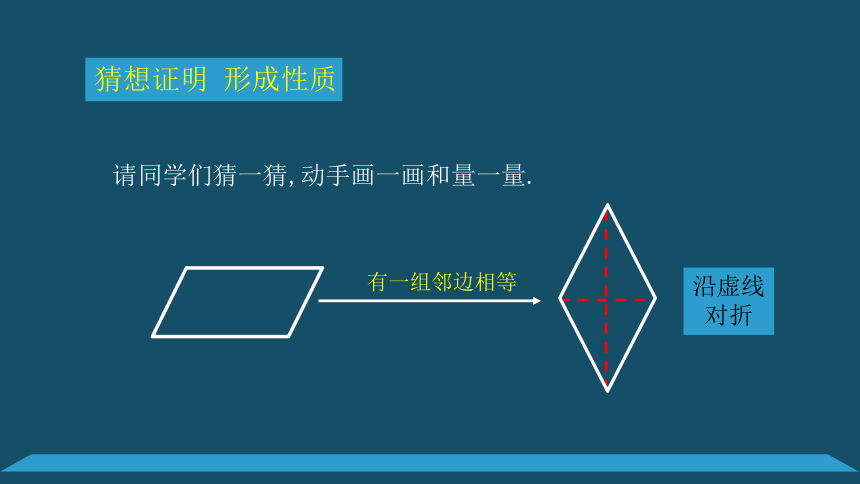
菱形是否具有一般平行四边形不具有的特殊性质呢?如果有,是哪些呢?
请同学们猜一猜,动手画一画和量一量.
猜想证明
形成性质
有一组邻边相等
沿虚线
对折
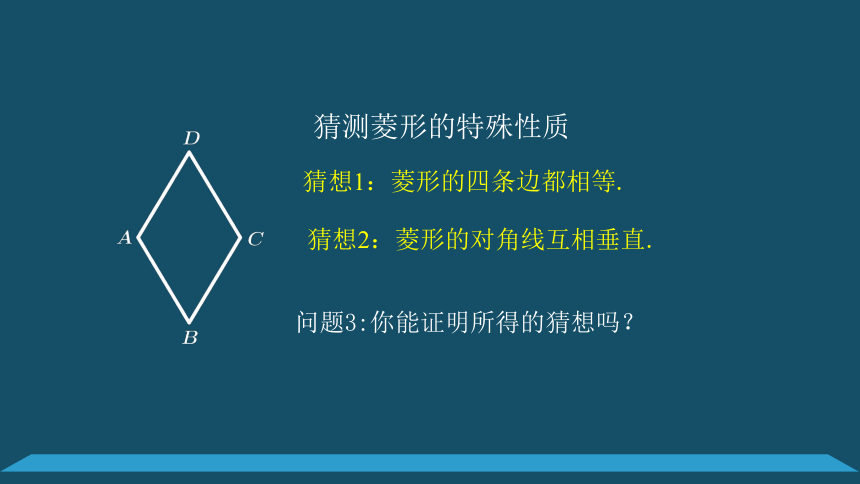
猜测菱形的特殊性质
猜想1:菱形的四条边都相等.
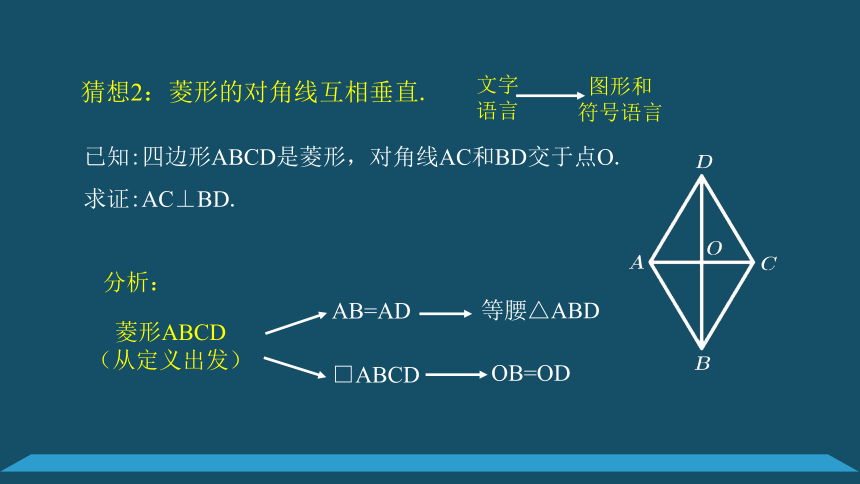
猜想2:菱形的对角线互相垂直.
问题3:你能证明所得的猜想吗?
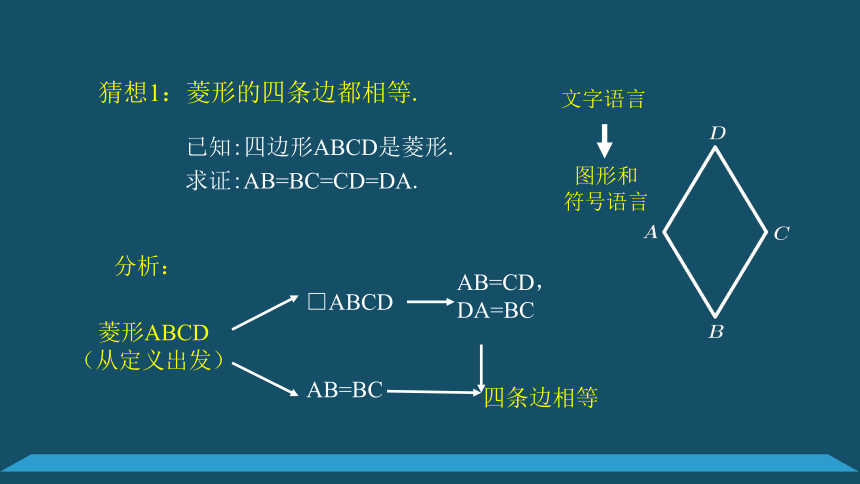
猜想1:菱形的四条边都相等.
已知:四边形ABCD是菱形.
求证:AB=BC=CD=DA.
文字语言
图形和
符号语言
菱形ABCD
(从定义出发)
□ABCD
AB=BC
AB=CD,
DA=BC
四条边相等
分析:
证明:∵四边形ABCD是菱形,
∴AB=CD,DA=BC,
AB=BC.
∴AB=BC=CD=DA.
猜想1:菱形的四条边都相等.
已知:四边形ABCD是菱形.
求证:AB=BC=CD=DA.
菱形性质定理1:菱形的四条边都相等.
符号语言:
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.
菱形性质定理
猜想2:菱形的对角线互相垂直.
已知:四边形ABCD是菱形,对角线AC和BD交于点O.
求证:AC⊥BD.
文字
语言
图形和
符号语言
菱形ABCD
(从定义出发)
□ABCD
AB=AD
等腰△ABD
OB=OD
分析:
分析:
等腰△ABD
OB=OD
三线合一
AO⊥BD,AO平分∠BAD
AC⊥BD,AC平分∠BAD
猜想2:菱形的对角线互相垂直.
已知:四边形ABCD是菱形,对角线AC和BD交于点O.
求证:AC⊥BD.
猜想2:菱形的对角线互相垂直,并且每一条对角线平分一组对角.
已知:四边形ABCD是菱形,对角线AC和BD交于点O.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
证明:∵四边形ABCD是菱形,
∴AB=AD,OB=OD.
∴
AC⊥BD,AC平分∠BAD.
同理可证AC平分∠BCD,BD平分∠ABC和∠ADC.
菱形性质定理2:菱形的对角线互相垂直,
并且每一条对角线平分一组对角.
符号语言:
∵四边形ABCD是菱形,对角线AC和BD交于点O,
∴AC⊥BD,AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
菱形性质定理
问题4:菱形是轴对称图形吗?如果是,它的对称轴是什么?
(1)菱形是轴对称图形.
(2)菱形有两条对称轴,
它们分别是两条对角线所在的直线.
菱形的性质
菱形的两组对角分别相等
菱形的对角线互相垂直平分,并且
每一条对角线平分一组对角
菱形的四条边都相等且两组对边分别平行
菱形是轴对称图形
边
角
对角线
对称性
运用性质
解决问题
(1)如图,四边形ABCD是菱形,AB=5cm,则该菱形的周长为_____cm.
例1
填空.
菱形的四条边都相等
周长=4AB=20cm
20
AB=5cm
分析:
(2)如图,四边形ABCD是菱形,∠DCB=150°,则∠ADB=______°.
菱形的两组对边分别平行
∠ADC=180°-∠DCB=
180°-
150°
=30°
AD∥BC
分析:
例1
填空.
菱形的每一条对角线平分一组对角
∠ADB=
∠ADC=
15°
15
(3)如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,则该菱形的边长是_____.
菱形的对角线互相平分
AO=
AC=3,
DO=
BD=4
分析:
例1
填空.
菱形的对角线互相垂直
在Rt△
AOD中,
AD=
5
3
4
例2
如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,求该菱形的面积.
菱形ABCD
分析:
AC⊥BD
AO=CO=
AC=3
对角线互相垂直
对角线互相平分
菱形ABCD
拆分
△ABD和△CBD
△ABD和△CBD的面积
菱形ABCD的面积
BD=8
解:∵四边形ABCD是菱形,AC=6,BD=8,
∴AC⊥BD,
AO=CO=
AC=
3.
例2
如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,求该菱形的面积.
∴菱形ABCD的面积=△ABD的面积+△CBD的面积
=
BD.AO
+
BD.CO
分析:
菱形ABCD
拆分
△ADC和△ABC
菱形ABCD
拆分
Rt△ADO,
Rt△CDO,
Rt△ABO,
Rt△CBO
例2
如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,求该菱形的面积.
菱形面积问题
三角形面积问题
对角线
变式:如图,菱形ABCD的对角线AC和BD交于点O,AC=a,
BD=b,求该菱形的面积.
解:菱形ABCD的面积
=△ABD的面积+△CBD的面积
=
BD×AO
+
BD×CO
=
BD×
(AO+CO)
=
BD×AC
=
ab
菱形的面积等于两条
对角线乘积的一半.
菱形的面积
(菱形特有面积计算公式)
底×高
两条对角线乘积的一半
解:∵四边形ABCD是菱形,∴OC=OA=2,AB=BC.
∵点C在y轴负半轴上,∴点C的坐标为(0,-2).
例3
如图,平面直角坐标系中,菱形ABCD,∠ABC=60°,点A的坐标为(0,2).
求B,C,D各点的坐标.
(0,2)
又∵∠ABC=60°,AC=4,∴AB=BC=AC=4.
∴OD=OB=
∵点B在x轴负半轴上,点D在x轴正半轴上,
∴点B的坐标为(
,0),
点D的坐标为(
,0).
等边三角形
直角三角形
菱形
坐标
数形结合
例3
如图,平面直角坐标系中,菱形ABCD,∠ABC=60°,点A的坐标为(0,2).
求B,C,D各点的坐标.
(0,2)
1.本节课你学习了什么知识?
课堂总结
菱形的性质
菱形的两组对角分别相等
菱形的对角线互相垂直平分,并且每一条对角线平分一组对角
菱形的四条边都相等且两组对边分别平行
菱形是轴对称图形
边
角
对角线
对称性
2.本节课你感受到了哪些数学思想方法?
(1)从一般到特殊:
平行四边形
菱形.
有一组邻边相等
(3)从特殊到一般:
(2)转化思想:
菱形的面积等于两条对角线乘积的一半.
将四边形问题转化为三角形问题.
课堂总结
3.本节课你感悟到的解题思路是什么?
4.本节课的研究过程给你的学习带来什么启示呢?
菱形
三角形
等腰三角形
直角三角形
等边三角形
全等三角形
课堂总结
课后作业
1.已知,菱形ABCD中,AB=4cm,∠ABC=60°,求菱形ABCD的面积.
2.已知,一个菱形的两条对角线的长分别为5cm和12cm,求该菱形的周长和面积.
课后作业
3.如图,菱形ABCD的对角线AC和BD交于点O,过点D作DE∥AC,且DE=OC,连接CE,OE,AE,若菱形ABCD的边长等于4,∠ABC=60°,求AE的长.
再
见
18.2.2.1
菱形的性质
学习目标
1
2
3
理解菱形的概念,会用菱形的性质解决简单的问题
体会几何图形研究的一般步骤和方法
通过探究和应用的过程提高几何直观能力和推理能力
学习重难点
重点
难点
菱形的性质及应用
菱形性质的探索及面积公式的推导
提出问题
引发思考
生活中美丽的菱形图案
菱形是特殊的平行四边形
平行四边形
菱形
有一组邻边相等
菱形的定义:
有一组邻边相等的平行四边形是菱形.
问题1:平行四边形的边特殊化得到什么图形呢?
问题2:菱形作为特殊的平行四边形,具有平行四边形的所有性质.
菱形是否具有一般平行四边形不具有的特殊性质呢?如果有,是哪些呢?
请同学们猜一猜,动手画一画和量一量.
猜想证明
形成性质
有一组邻边相等
沿虚线
对折
猜测菱形的特殊性质
猜想1:菱形的四条边都相等.
猜想2:菱形的对角线互相垂直.
问题3:你能证明所得的猜想吗?
猜想1:菱形的四条边都相等.
已知:四边形ABCD是菱形.
求证:AB=BC=CD=DA.
文字语言
图形和
符号语言
菱形ABCD
(从定义出发)
□ABCD
AB=BC
AB=CD,
DA=BC
四条边相等
分析:
证明:∵四边形ABCD是菱形,
∴AB=CD,DA=BC,
AB=BC.
∴AB=BC=CD=DA.
猜想1:菱形的四条边都相等.
已知:四边形ABCD是菱形.
求证:AB=BC=CD=DA.
菱形性质定理1:菱形的四条边都相等.
符号语言:
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.
菱形性质定理
猜想2:菱形的对角线互相垂直.
已知:四边形ABCD是菱形,对角线AC和BD交于点O.
求证:AC⊥BD.
文字
语言
图形和
符号语言
菱形ABCD
(从定义出发)
□ABCD
AB=AD
等腰△ABD
OB=OD
分析:
分析:
等腰△ABD
OB=OD
三线合一
AO⊥BD,AO平分∠BAD
AC⊥BD,AC平分∠BAD
猜想2:菱形的对角线互相垂直.
已知:四边形ABCD是菱形,对角线AC和BD交于点O.
求证:AC⊥BD.
猜想2:菱形的对角线互相垂直,并且每一条对角线平分一组对角.
已知:四边形ABCD是菱形,对角线AC和BD交于点O.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
证明:∵四边形ABCD是菱形,
∴AB=AD,OB=OD.
∴
AC⊥BD,AC平分∠BAD.
同理可证AC平分∠BCD,BD平分∠ABC和∠ADC.
菱形性质定理2:菱形的对角线互相垂直,
并且每一条对角线平分一组对角.
符号语言:
∵四边形ABCD是菱形,对角线AC和BD交于点O,
∴AC⊥BD,AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
菱形性质定理
问题4:菱形是轴对称图形吗?如果是,它的对称轴是什么?
(1)菱形是轴对称图形.
(2)菱形有两条对称轴,
它们分别是两条对角线所在的直线.
菱形的性质
菱形的两组对角分别相等
菱形的对角线互相垂直平分,并且
每一条对角线平分一组对角
菱形的四条边都相等且两组对边分别平行
菱形是轴对称图形
边
角
对角线
对称性
运用性质
解决问题
(1)如图,四边形ABCD是菱形,AB=5cm,则该菱形的周长为_____cm.
例1
填空.
菱形的四条边都相等
周长=4AB=20cm
20
AB=5cm
分析:
(2)如图,四边形ABCD是菱形,∠DCB=150°,则∠ADB=______°.
菱形的两组对边分别平行
∠ADC=180°-∠DCB=
180°-
150°
=30°
AD∥BC
分析:
例1
填空.
菱形的每一条对角线平分一组对角
∠ADB=
∠ADC=
15°
15
(3)如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,则该菱形的边长是_____.
菱形的对角线互相平分
AO=
AC=3,
DO=
BD=4
分析:
例1
填空.
菱形的对角线互相垂直
在Rt△
AOD中,
AD=
5
3
4
例2
如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,求该菱形的面积.
菱形ABCD
分析:
AC⊥BD
AO=CO=
AC=3
对角线互相垂直
对角线互相平分
菱形ABCD
拆分
△ABD和△CBD
△ABD和△CBD的面积
菱形ABCD的面积
BD=8
解:∵四边形ABCD是菱形,AC=6,BD=8,
∴AC⊥BD,
AO=CO=
AC=
3.
例2
如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,求该菱形的面积.
∴菱形ABCD的面积=△ABD的面积+△CBD的面积
=
BD.AO
+
BD.CO
分析:
菱形ABCD
拆分
△ADC和△ABC
菱形ABCD
拆分
Rt△ADO,
Rt△CDO,
Rt△ABO,
Rt△CBO
例2
如图,菱形ABCD的对角线AC和BD交于点O,AC=6,BD=8,求该菱形的面积.
菱形面积问题
三角形面积问题
对角线
变式:如图,菱形ABCD的对角线AC和BD交于点O,AC=a,
BD=b,求该菱形的面积.
解:菱形ABCD的面积
=△ABD的面积+△CBD的面积
=
BD×AO
+
BD×CO
=
BD×
(AO+CO)
=
BD×AC
=
ab
菱形的面积等于两条
对角线乘积的一半.
菱形的面积
(菱形特有面积计算公式)
底×高
两条对角线乘积的一半
解:∵四边形ABCD是菱形,∴OC=OA=2,AB=BC.
∵点C在y轴负半轴上,∴点C的坐标为(0,-2).
例3
如图,平面直角坐标系中,菱形ABCD,∠ABC=60°,点A的坐标为(0,2).
求B,C,D各点的坐标.
(0,2)
又∵∠ABC=60°,AC=4,∴AB=BC=AC=4.
∴OD=OB=
∵点B在x轴负半轴上,点D在x轴正半轴上,
∴点B的坐标为(
,0),
点D的坐标为(
,0).
等边三角形
直角三角形
菱形
坐标
数形结合
例3
如图,平面直角坐标系中,菱形ABCD,∠ABC=60°,点A的坐标为(0,2).
求B,C,D各点的坐标.
(0,2)
1.本节课你学习了什么知识?
课堂总结
菱形的性质
菱形的两组对角分别相等
菱形的对角线互相垂直平分,并且每一条对角线平分一组对角
菱形的四条边都相等且两组对边分别平行
菱形是轴对称图形
边
角
对角线
对称性
2.本节课你感受到了哪些数学思想方法?
(1)从一般到特殊:
平行四边形
菱形.
有一组邻边相等
(3)从特殊到一般:
(2)转化思想:
菱形的面积等于两条对角线乘积的一半.
将四边形问题转化为三角形问题.
课堂总结
3.本节课你感悟到的解题思路是什么?
4.本节课的研究过程给你的学习带来什么启示呢?
菱形
三角形
等腰三角形
直角三角形
等边三角形
全等三角形
课堂总结
课后作业
1.已知,菱形ABCD中,AB=4cm,∠ABC=60°,求菱形ABCD的面积.
2.已知,一个菱形的两条对角线的长分别为5cm和12cm,求该菱形的周长和面积.
课后作业
3.如图,菱形ABCD的对角线AC和BD交于点O,过点D作DE∥AC,且DE=OC,连接CE,OE,AE,若菱形ABCD的边长等于4,∠ABC=60°,求AE的长.
再
见
