2020-2021学年人教版七年级数学下册第九章不等式与不等式组复习教案
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册第九章不等式与不等式组复习教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 23:13:29 | ||
图片预览

文档简介
授课年级
七年级
学科
数学
课题
不等式与不等式组(1)
任课教师
课型
问题生成解决课
课时
1课时
授课时间
教学目标
1、知识与能力:能够根据具体问题中的大小关系了解不等式的意义和基本性质.
2、过程与方法:会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集.3、情感态度与价值观.会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.
重点难点
重点:能熟练的解一元一次不等式与一元一次不等式组难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想
教学方法
讨论法、练习法。
关键问题
能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想
教学准备
1.《问题导读生成评价单》2.《问题训练扩展评价单》
教学过程
教学环节
时间
创设情景(教学内容)
教师行为
期望的学生行为
创设情景问题导入
3-5分钟
问题1不等式,不等式的解与解集不等式的基本性质。问题2一元一次不等式解一元一次不等式的一般步骤:一元一次不等式组。
教师提出问题,导入新课。
带着问题合作交流
自主合作解决问题
5-10分钟
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
简单引导
尽量独立完成
合作探究交流解决问题
15-20分钟
合作探究1:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多.
组织学生讨论;评价、补充。
1、合作交流解决问题;2、展示学习成果;3、成果共享,相互补充。
问题训练
3-8分钟
解不等式:解不等式组并把它的解集在数轴上表示出来.
巡回个别指导,评价,补充讲解。
合作解决问题,小组展示。
总结提升
1-3分钟
1.在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。2.解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是:①等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质。②不等式组解集的确定方法。3.求不等式(组)的特殊解
不等式(组)的解往往是无数多个,但有时解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集,然后再找到相应的答案。在这类题目中,要注意对数形结合思想的应用
点拨、补充;评价
学生自己总结,教师补充。
板书设计
不等式与不等式组(1)
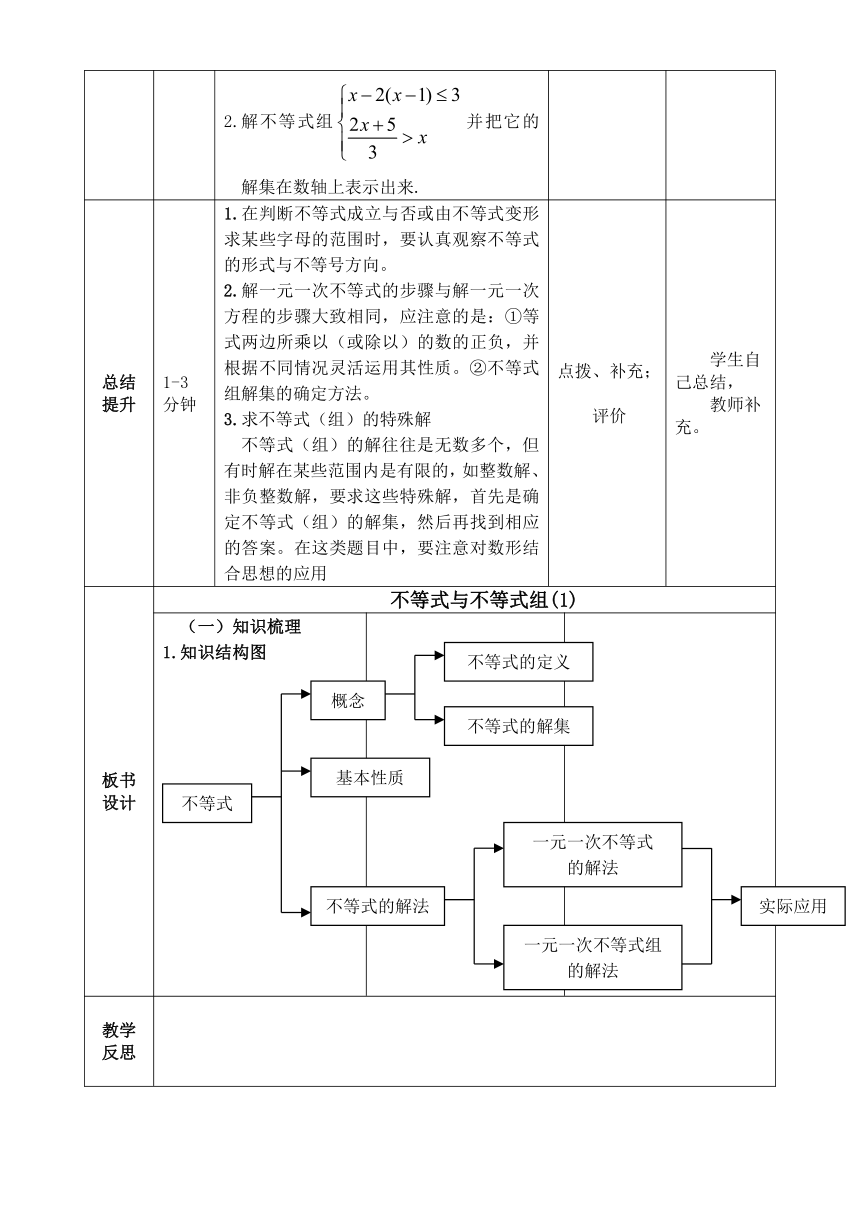
(一)知识梳理1.知识结构图
教学反思
《不等式与不等式组(1)》——问题导读生成评价单
班级:
姓名:
设计者:
1.不等式
用
连接起来的式子叫做不等式.
常见的不等号有五种:
2.不等式的解与解集
不等式的解:
不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向
,小向
。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
3.不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果,那么
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果,那么(或)
(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果那么(或)
4.一元一次不等式
只含有一个未知数,且未知数的次数是
.系数不等于0的不等式叫做一元一次不等式.
注:一元一次不等式的一般形式是ax+b>O或ax+b5.解一元一次不等式的一般步骤:
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)化系数为1.
说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个
时,不等号
必须改变,这是解不等式时最容易出错的地方.
6.一元一次不等式组
含有
几个一元一次不等式所组成的不等式组,叫做一元一次不等式组.
7.一元一次不等式组的解集
一元一次不等式组中,
.叫做这个一元一次不等式组的解集.
8.
不等式组解集的确定方法,可以归纳为以下四种类型(设a>b)
不等式组
图示
解集
1.解不等式:
2
解不等式组并把它的解集在数轴上表示出来.
3.
已知关于的方程5-2=3-6+1的解满足-3<≤2,求的整数值.
你还有不懂的问题是:
自己评价
小组长评价
老师评价
《不等式与不等式组(1)》——问题拓展训练评价单
班级:
姓名:
设计者:
1.求代数式3(+1)的值不小于5-9的值的最大的整数.
2.解不等式组,并把它的解集在数轴上表示出来.
3.三角形三边长分别为3、、8,求的取值范围
4.已知关于的不等式组无解,求的取值范围.
你还有不懂的问题是:
自己评价
小组长评价
老师评价
概念
基本性质
不等式的定义
不等式的解法
一元一次不等式
的解法
一元一次不等式组
的解法
不等式
实际应用
不等式的解集
七年级
学科
数学
课题
不等式与不等式组(1)
任课教师
课型
问题生成解决课
课时
1课时
授课时间
教学目标
1、知识与能力:能够根据具体问题中的大小关系了解不等式的意义和基本性质.
2、过程与方法:会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集.3、情感态度与价值观.会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.
重点难点
重点:能熟练的解一元一次不等式与一元一次不等式组难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想
教学方法
讨论法、练习法。
关键问题
能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想
教学准备
1.《问题导读生成评价单》2.《问题训练扩展评价单》
教学过程
教学环节
时间
创设情景(教学内容)
教师行为
期望的学生行为
创设情景问题导入
3-5分钟
问题1不等式,不等式的解与解集不等式的基本性质。问题2一元一次不等式解一元一次不等式的一般步骤:一元一次不等式组。
教师提出问题,导入新课。
带着问题合作交流
自主合作解决问题
5-10分钟
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
简单引导
尽量独立完成
合作探究交流解决问题
15-20分钟
合作探究1:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多.
组织学生讨论;评价、补充。
1、合作交流解决问题;2、展示学习成果;3、成果共享,相互补充。
问题训练
3-8分钟
解不等式:解不等式组并把它的解集在数轴上表示出来.
巡回个别指导,评价,补充讲解。
合作解决问题,小组展示。
总结提升
1-3分钟
1.在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。2.解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是:①等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质。②不等式组解集的确定方法。3.求不等式(组)的特殊解
不等式(组)的解往往是无数多个,但有时解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集,然后再找到相应的答案。在这类题目中,要注意对数形结合思想的应用
点拨、补充;评价
学生自己总结,教师补充。
板书设计
不等式与不等式组(1)
(一)知识梳理1.知识结构图
教学反思
《不等式与不等式组(1)》——问题导读生成评价单
班级:
姓名:
设计者:
1.不等式
用
连接起来的式子叫做不等式.
常见的不等号有五种:
2.不等式的解与解集
不等式的解:
不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向
,小向
。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
3.不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果,那么
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果,那么(或)
(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果那么(或)
4.一元一次不等式
只含有一个未知数,且未知数的次数是
.系数不等于0的不等式叫做一元一次不等式.
注:一元一次不等式的一般形式是ax+b>O或ax+b
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)化系数为1.
说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个
时,不等号
必须改变,这是解不等式时最容易出错的地方.
6.一元一次不等式组
含有
几个一元一次不等式所组成的不等式组,叫做一元一次不等式组.
7.一元一次不等式组的解集
一元一次不等式组中,
.叫做这个一元一次不等式组的解集.
8.
不等式组解集的确定方法,可以归纳为以下四种类型(设a>b)
不等式组
图示
解集
1.解不等式:
2
解不等式组并把它的解集在数轴上表示出来.
3.
已知关于的方程5-2=3-6+1的解满足-3<≤2,求的整数值.
你还有不懂的问题是:
自己评价
小组长评价
老师评价
《不等式与不等式组(1)》——问题拓展训练评价单
班级:
姓名:
设计者:
1.求代数式3(+1)的值不小于5-9的值的最大的整数.
2.解不等式组,并把它的解集在数轴上表示出来.
3.三角形三边长分别为3、、8,求的取值范围
4.已知关于的不等式组无解,求的取值范围.
你还有不懂的问题是:
自己评价
小组长评价
老师评价
概念
基本性质
不等式的定义
不等式的解法
一元一次不等式
的解法
一元一次不等式组
的解法
不等式
实际应用
不等式的解集
