2020-2021学年人教版数学七年级下册:6.1.3平方根 课件(26张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册:6.1.3平方根 课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 10:11:17 | ||
图片预览








文档简介
(共26张PPT)
6.1.3
平
方
根
人教版数学七年级下册
第六章
实
数
理解平方根的概念,会用符号表示一个数的平方根。
算术平方根与平方根的区别与联系。
会求一个数的平方根。
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有请
求出它们的算术平方根.
100;1;
;
0;
-0.0025;
(-3)2
;
-25;
回顾与思考
(1)32=
,(-3)2=
;
(2)
,
;
(3)0.82=
,(-0.8)2=
.
9
0.64
0.64
3.
填空
9
思考:反过来,如果已知一个数的平方,怎样求这
个数?
回顾与思考
问题
如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于
,
所以这个数是3或-3.
3和-3互为相反数,会不会是巧合呢?
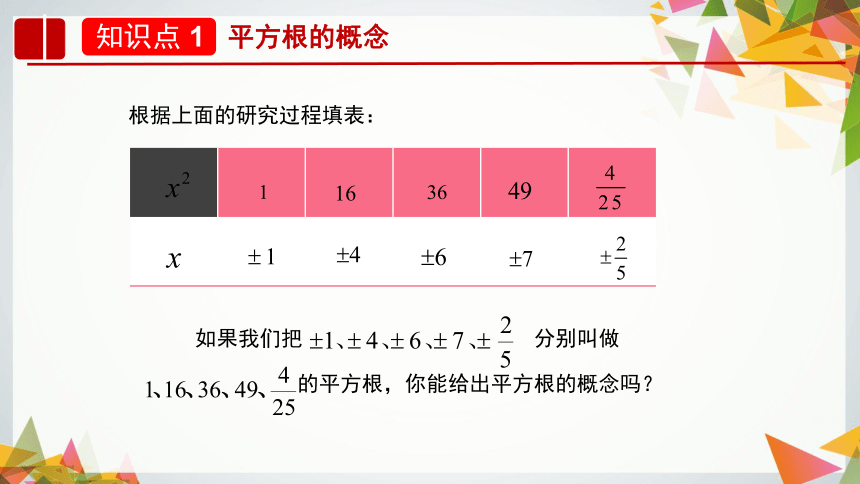
根据上面的研究过程填表:
如果我们把
分别叫做
的平方根,你能给出平方根的概念吗?
根据上述问题,即要找出一个数,使它的平方等于给定的数.我们抽象出下述概念:
如果有一个数x,使得x
2=a,那么我们把x
叫作a
的一个平方根,也叫作二次方根.
如果x
是正数a
的一个平方根,那么a的平方根有且只有两个:x
与-x.即平方根互为相反数.
平方根的性质:
例如:
(±1)2=1,1的平方根为±1.
一、平方根的概念
由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.
由于同号两数相乘得正数,所以任何一个数的平方都不会是负数,因此-9没有平方根,进一步的,所有的负数都没有平方根.
在上面的问题中,我们求平方根的数都是正数.
思考
1.零有平方根吗?如果有,它的平方根是多少?
2.-9有平方根吗?负数有平方根吗?
总结归纳
1.一个正数有两个平方根,它们互为相反数;
2.零的平方根是0;
3.负数没有平方根.
判断下列各数是否有平方根,请说明理由.
-4;
0;
0.000001;
100;
练一练:
+1
-1
+2
-2
+3
-3
1
4
9
平方
已知一个数,求它的平方的运算,叫作平方运算.
回顾平方的概念
+1
-1
+2
-2
+3
-3
1
4
9
?运算
反之,已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
二、开平方的概念
表示a的正的平方根
表示a的负的平方根
记作
a﹙a≥0﹚的平方根表示为
一个非负数的平方根的表示方法:
(算术平方根)
三、平方根的数学符号表示
说一说
各表示什么意义?
表示7的正的平方根(即算术平方根)
表示7的负的平方根
表示7的平方根
平方根与算术平方根的联系:
(1)具有包含关系:平方根包含算术平方根,算术
平方根是平方根的一种;
(2)存在条件相同:只非负数才有平方根和算术平方根;
(3)0的平方根和算术平方根都是0.
四、平方根与算术平方根
平方根与算术平方根的区别:
(1)定义不同:如果一个数x的平方等于a,那么这个
数x叫做
a的平方根,如果一个正数x的平方等于a,
即x2
=a,那么这个正数x叫做a的算术平方根.
(2)个数不同:一个正数有两个平方根,而一个正
数的算术平方根只有一个;
(3)表示方法不同:正数a的算术平方根表示为
,
而正数a的平方根表示为±
.
四、平方根与算术平方根
算术平方根
平方根
区别
概念
如果一个正数x的平方等于a,即=a,那么这个正数x叫做a的算术平方根。
如果一个数的平方等于a,那么这个数就叫做a的平方根或二次方根,即如果=a,那么x叫做a的平方根。
表示方法
±
性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0
3)负数没有算术平方根
1)正数有两个平方根,且互为相反数;
2)0的平方根为0
3)负数没有平方根
求法
开平方后取非负的平方根
开平方
联系
1)a的取值范围相同,均为a≥0
2)平方根包含了算术平方根,即算术平方根是平方根中的一个(非负的)。
1、如果_____________等于a,那么这个数就叫做的平方根或二次方根;
2、非负数的平方根表示为______.
3、±中的a称为___
数,其中有意义的条件是_______;
4、一个正数有____个平方根,它们互为_____;0的平方根是___,负数______平方根.
5、平方根与算术平方根的联系与区别?
一个数的平方
0
±
被开方
a≥0
两
相反数
没有
例1
一个正数的两个平方根分别是2a+1和a-4,求这个数.
解:由于一个正数的两个平方根是2a+1和a-4,
则有2a+1+a-4=0,即3a-3=0,
解得a=1.
所以这个数为(2a+1)2=(2+1)2=9.
【点睛】一个正数有两个平方根,它们互为相反数.
例2
分别求下列各数的平方根:
36,
,1.21.
解:由于62=36,
因此36的平方根是6与-6.
36是正数
(1)36
有两个平方根
即
(2)
解:
由于
2=
,
有两个平方根
因此
的平方根是
与
.
即
解:
由于1.12=1.21,
有两个平方根
(3)1.21
因此1.21的平方根是1.1与-1.1.
即
例3:求下列各式的值:
解:(1)
;
(2)
;
(3)
.
1.下列各数:,,,,,,,其中有平方根的有(
)
A.个
B.个
C.个
D.个
【答案】B
【详解】
解:、=-3、=-625,化简之后都为负数,
、、、都为非负数,
∴有平方根的有4个.
故选B.
2.下列各式中,正确的是(
)
A.
B.
C.
D.
【答案】B
【详解】
;;;2,故选B.
3.若一个正数的平方根为和,则(
)
A.7
B.16
C.25
D.49
【答案】D
【详解】
∵一个正数x的平方根为和,
∴()+()=0,
解得:a=7.
∴=7,=-7,
∴x==49.
故选D.
4.下列运算中错误的有( )
①②,③,④=3
A.4个
B.3个
C.2个
D.1个
【答案】B
【详解】
①,故A正确;②,故B错误;
③,无法开方,故C错误;④±±3,故D错误.
错误的有3个.故选B.
5.已知2m﹣4与3m﹣1是同一个正数的两个平方根,则m的值是
__________
【答案】1
【解析】∵2m-4与3m-1是同一个正数的两个平方根,
∴2m-4+3m-1=0,
∴m=1.
故答案是1。
谢谢观看
6.1.3
平
方
根
人教版数学七年级下册
第六章
实
数
理解平方根的概念,会用符号表示一个数的平方根。
算术平方根与平方根的区别与联系。
会求一个数的平方根。
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有请
求出它们的算术平方根.
100;1;
;
0;
-0.0025;
(-3)2
;
-25;
回顾与思考
(1)32=
,(-3)2=
;
(2)
,
;
(3)0.82=
,(-0.8)2=
.
9
0.64
0.64
3.
填空
9
思考:反过来,如果已知一个数的平方,怎样求这
个数?
回顾与思考
问题
如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于
,
所以这个数是3或-3.
3和-3互为相反数,会不会是巧合呢?
根据上面的研究过程填表:
如果我们把
分别叫做
的平方根,你能给出平方根的概念吗?
根据上述问题,即要找出一个数,使它的平方等于给定的数.我们抽象出下述概念:
如果有一个数x,使得x
2=a,那么我们把x
叫作a
的一个平方根,也叫作二次方根.
如果x
是正数a
的一个平方根,那么a的平方根有且只有两个:x
与-x.即平方根互为相反数.
平方根的性质:
例如:
(±1)2=1,1的平方根为±1.
一、平方根的概念
由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.
由于同号两数相乘得正数,所以任何一个数的平方都不会是负数,因此-9没有平方根,进一步的,所有的负数都没有平方根.
在上面的问题中,我们求平方根的数都是正数.
思考
1.零有平方根吗?如果有,它的平方根是多少?
2.-9有平方根吗?负数有平方根吗?
总结归纳
1.一个正数有两个平方根,它们互为相反数;
2.零的平方根是0;
3.负数没有平方根.
判断下列各数是否有平方根,请说明理由.
-4;
0;
0.000001;
100;
练一练:
+1
-1
+2
-2
+3
-3
1
4
9
平方
已知一个数,求它的平方的运算,叫作平方运算.
回顾平方的概念
+1
-1
+2
-2
+3
-3
1
4
9
?运算
反之,已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
二、开平方的概念
表示a的正的平方根
表示a的负的平方根
记作
a﹙a≥0﹚的平方根表示为
一个非负数的平方根的表示方法:
(算术平方根)
三、平方根的数学符号表示
说一说
各表示什么意义?
表示7的正的平方根(即算术平方根)
表示7的负的平方根
表示7的平方根
平方根与算术平方根的联系:
(1)具有包含关系:平方根包含算术平方根,算术
平方根是平方根的一种;
(2)存在条件相同:只非负数才有平方根和算术平方根;
(3)0的平方根和算术平方根都是0.
四、平方根与算术平方根
平方根与算术平方根的区别:
(1)定义不同:如果一个数x的平方等于a,那么这个
数x叫做
a的平方根,如果一个正数x的平方等于a,
即x2
=a,那么这个正数x叫做a的算术平方根.
(2)个数不同:一个正数有两个平方根,而一个正
数的算术平方根只有一个;
(3)表示方法不同:正数a的算术平方根表示为
,
而正数a的平方根表示为±
.
四、平方根与算术平方根
算术平方根
平方根
区别
概念
如果一个正数x的平方等于a,即=a,那么这个正数x叫做a的算术平方根。
如果一个数的平方等于a,那么这个数就叫做a的平方根或二次方根,即如果=a,那么x叫做a的平方根。
表示方法
±
性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0
3)负数没有算术平方根
1)正数有两个平方根,且互为相反数;
2)0的平方根为0
3)负数没有平方根
求法
开平方后取非负的平方根
开平方
联系
1)a的取值范围相同,均为a≥0
2)平方根包含了算术平方根,即算术平方根是平方根中的一个(非负的)。
1、如果_____________等于a,那么这个数就叫做的平方根或二次方根;
2、非负数的平方根表示为______.
3、±中的a称为___
数,其中有意义的条件是_______;
4、一个正数有____个平方根,它们互为_____;0的平方根是___,负数______平方根.
5、平方根与算术平方根的联系与区别?
一个数的平方
0
±
被开方
a≥0
两
相反数
没有
例1
一个正数的两个平方根分别是2a+1和a-4,求这个数.
解:由于一个正数的两个平方根是2a+1和a-4,
则有2a+1+a-4=0,即3a-3=0,
解得a=1.
所以这个数为(2a+1)2=(2+1)2=9.
【点睛】一个正数有两个平方根,它们互为相反数.
例2
分别求下列各数的平方根:
36,
,1.21.
解:由于62=36,
因此36的平方根是6与-6.
36是正数
(1)36
有两个平方根
即
(2)
解:
由于
2=
,
有两个平方根
因此
的平方根是
与
.
即
解:
由于1.12=1.21,
有两个平方根
(3)1.21
因此1.21的平方根是1.1与-1.1.
即
例3:求下列各式的值:
解:(1)
;
(2)
;
(3)
.
1.下列各数:,,,,,,,其中有平方根的有(
)
A.个
B.个
C.个
D.个
【答案】B
【详解】
解:、=-3、=-625,化简之后都为负数,
、、、都为非负数,
∴有平方根的有4个.
故选B.
2.下列各式中,正确的是(
)
A.
B.
C.
D.
【答案】B
【详解】
;;;2,故选B.
3.若一个正数的平方根为和,则(
)
A.7
B.16
C.25
D.49
【答案】D
【详解】
∵一个正数x的平方根为和,
∴()+()=0,
解得:a=7.
∴=7,=-7,
∴x==49.
故选D.
4.下列运算中错误的有( )
①②,③,④=3
A.4个
B.3个
C.2个
D.1个
【答案】B
【详解】
①,故A正确;②,故B错误;
③,无法开方,故C错误;④±±3,故D错误.
错误的有3个.故选B.
5.已知2m﹣4与3m﹣1是同一个正数的两个平方根,则m的值是
__________
【答案】1
【解析】∵2m-4与3m-1是同一个正数的两个平方根,
∴2m-4+3m-1=0,
∴m=1.
故答案是1。
谢谢观看
