五年级数学下册课件 7解决问题的策略-苏教版 (31页PPT)
文档属性
| 名称 | 五年级数学下册课件 7解决问题的策略-苏教版 (31页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 13:34:11 | ||
图片预览



文档简介
(共31张PPT)
苏教版五年级下册
解决问题的策略---转化
《曹冲称象》
1.曹冲把大象的体重换成什么的重量?
2.曹冲称大象体重的时候为什么要在船上作个标记?
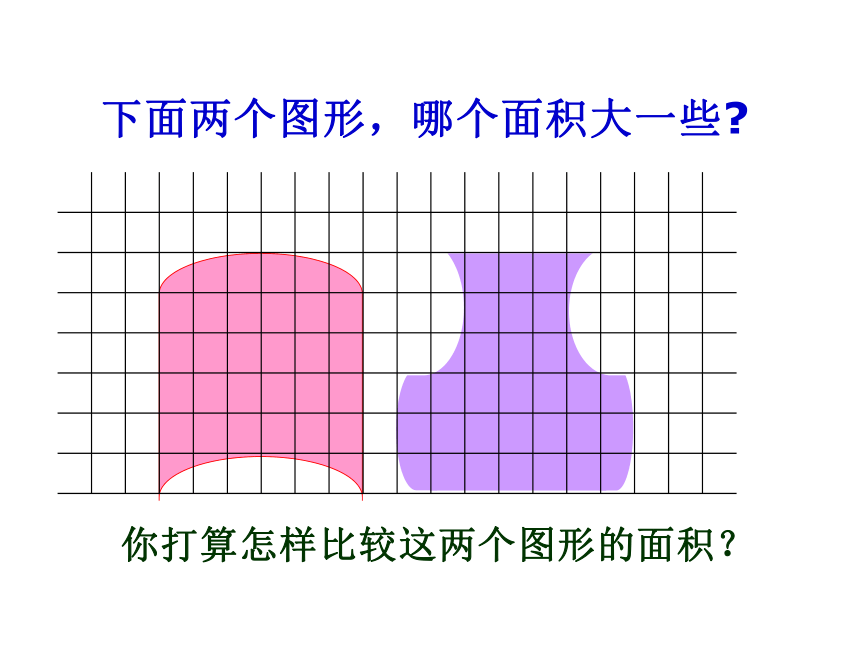
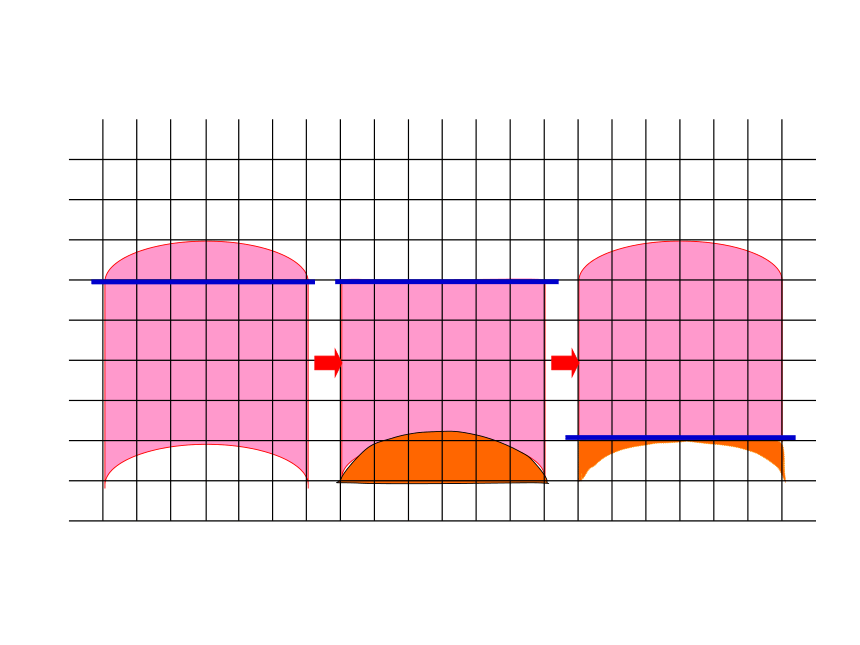
下面两个图形,哪个面积大一些?
你打算怎样比较这两个图形的面积?
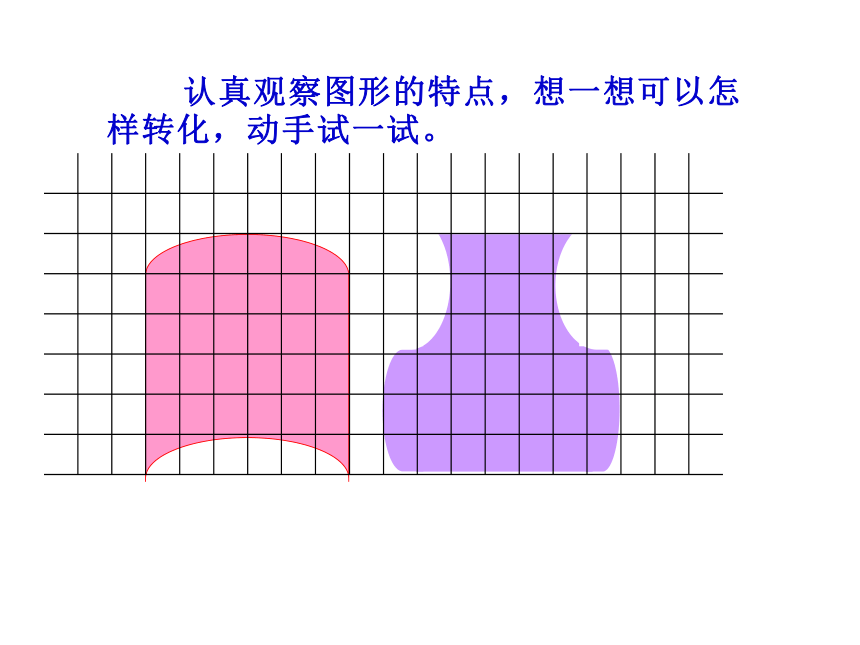
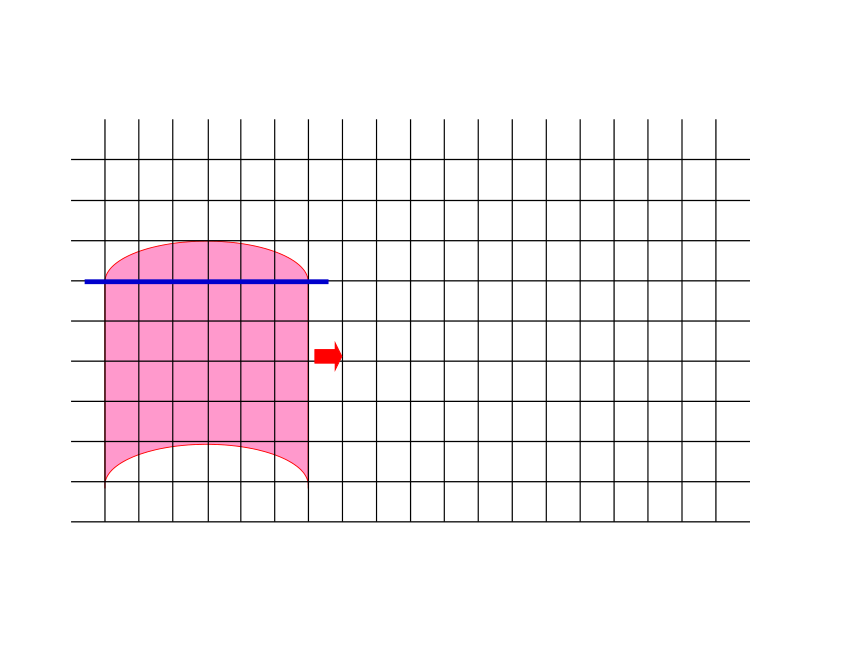
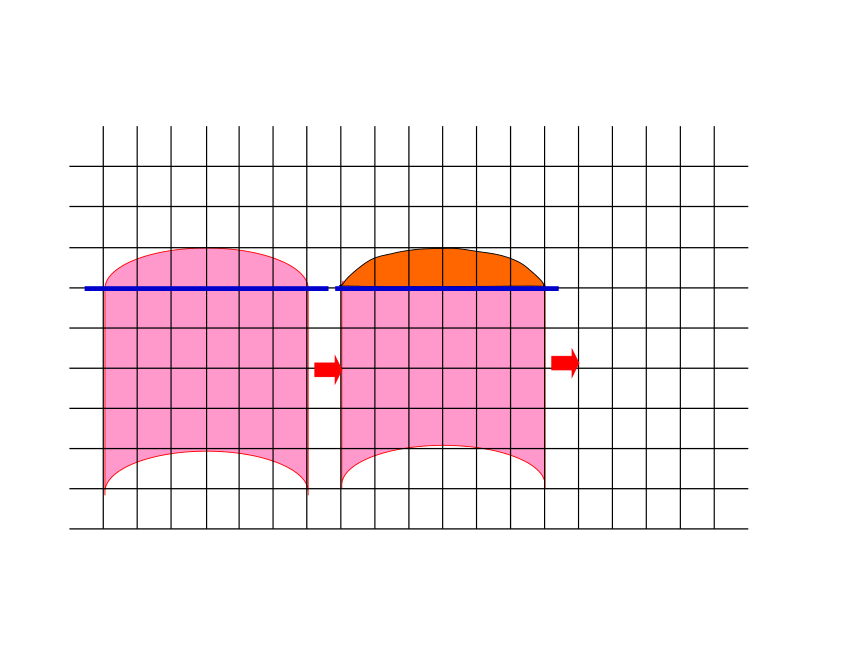
认真观察图形的特点,想一想可以怎样转化,动手试一试。
6
5
6
5
5×6=30
5×6=30
转化后的两个图形面积相等,所以原来的两个图形的面积相等。
在以前的学习中,我们运用转化的
策略解决过哪些问题?
返回
用两个完全相同的三角形拼成一个平行四边形。
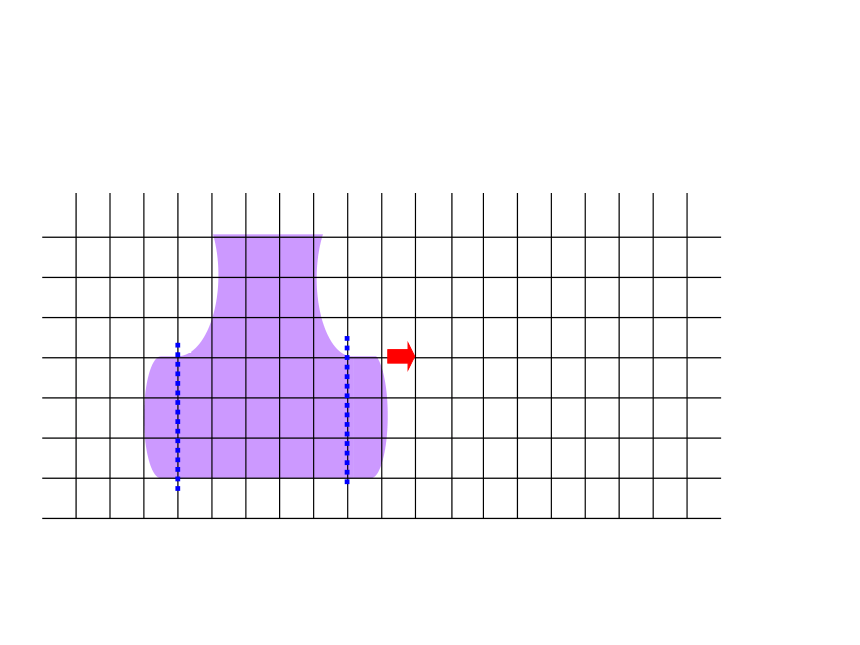
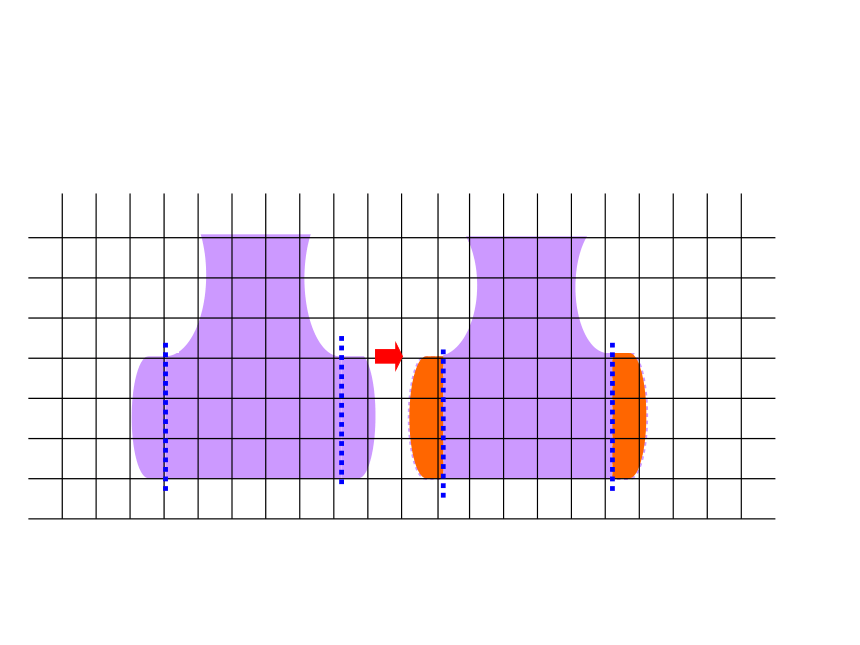
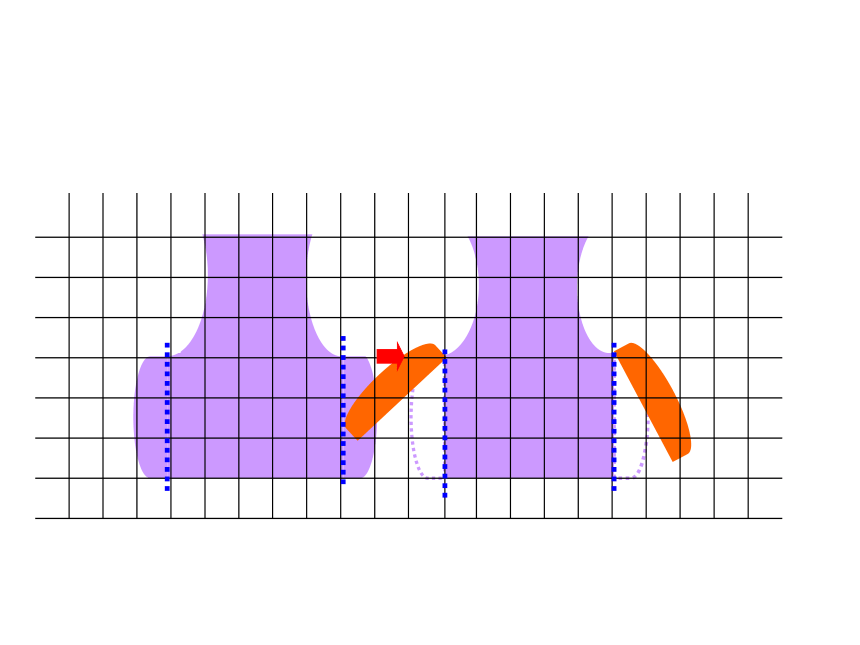
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?
1.用分数表示各图中的涂色部分。
练一练
(
)
(
)
(
)
(
)
4
1
2
1
5
8
2.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
(3+4)×2=14(厘米)
(5+3)×2=16(厘米)
3.一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
45米
27米
43米
25米
43×25=1075(平方米)
有位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。”学完今天这节课后你如何理解这句话?
学习数学的过程就是不断转化的过程。将复杂转化为简单,陌生转化为熟悉,抽象转化为具体,未知转化为已知。所以,掌握转化的策略,对学好数学至关重要。
有个太太,有两个女儿,大女儿是卖伞的,小女儿是开洗衣店的。晴天,她担心大女儿的伞卖不出去;雨天,她担心小女儿洗的衣服晒不干,整天忧心忡忡,很不开心。该怎样劝老太太呢?
有些时候,换个角度去想问题,你会发现真的很不一样!其实自己快乐与否,重在心态。只要你用乐观的心态去面对,无论任何事情,都会是快乐的!希望大家在生活中快乐地转化,在数学中灵活地转化!
回顾解决问题的过程,你有什么体会?
有些不规则的图形可以转化成熟悉的简单的图形。
图形转化时可以运用平移、旋转等方法。
转化后的图形与转化前相比,形状变了,大小没有变。
有一次,爱迪生请他的助手帮忙测量一个无芯灯泡的容积,助手对着这只梨形的灯泡苦思冥想,一会儿拿尺子量尺寸,一会儿又画出各种草图,可忙乎了老半天都没有个结果。这时候爱迪生走过来,一看这情形笑了“何必这么麻烦呢,你把这只灯泡装满水,再把水倒入量杯中,灯泡的容积不就转化成水的体积被测量出来了吗?”听了这番话,助手恍然大悟,于是他依照这个办法,很快就把灯泡的容积测量出来了。
提问:
⑴
听了这则故事以后,你知道大发明家爱迪生是如何测出梨形灯泡的容积的吗?他有没有实际去测灯泡的容积?
⑵
他去测了什么?
⑶
爱迪生要测的是灯泡的容积,为什么变成了测水的体积呢?
⑷
爱迪生实际上是运用了一种策略,你知道是什么策略吗?
苏教版五年级下册
解决问题的策略---转化
《曹冲称象》
1.曹冲把大象的体重换成什么的重量?
2.曹冲称大象体重的时候为什么要在船上作个标记?
下面两个图形,哪个面积大一些?
你打算怎样比较这两个图形的面积?
认真观察图形的特点,想一想可以怎样转化,动手试一试。
6
5
6
5
5×6=30
5×6=30
转化后的两个图形面积相等,所以原来的两个图形的面积相等。
在以前的学习中,我们运用转化的
策略解决过哪些问题?
返回
用两个完全相同的三角形拼成一个平行四边形。
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?
1.用分数表示各图中的涂色部分。
练一练
(
)
(
)
(
)
(
)
4
1
2
1
5
8
2.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
(3+4)×2=14(厘米)
(5+3)×2=16(厘米)
3.一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
45米
27米
43米
25米
43×25=1075(平方米)
有位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。”学完今天这节课后你如何理解这句话?
学习数学的过程就是不断转化的过程。将复杂转化为简单,陌生转化为熟悉,抽象转化为具体,未知转化为已知。所以,掌握转化的策略,对学好数学至关重要。
有个太太,有两个女儿,大女儿是卖伞的,小女儿是开洗衣店的。晴天,她担心大女儿的伞卖不出去;雨天,她担心小女儿洗的衣服晒不干,整天忧心忡忡,很不开心。该怎样劝老太太呢?
有些时候,换个角度去想问题,你会发现真的很不一样!其实自己快乐与否,重在心态。只要你用乐观的心态去面对,无论任何事情,都会是快乐的!希望大家在生活中快乐地转化,在数学中灵活地转化!
回顾解决问题的过程,你有什么体会?
有些不规则的图形可以转化成熟悉的简单的图形。
图形转化时可以运用平移、旋转等方法。
转化后的图形与转化前相比,形状变了,大小没有变。
有一次,爱迪生请他的助手帮忙测量一个无芯灯泡的容积,助手对着这只梨形的灯泡苦思冥想,一会儿拿尺子量尺寸,一会儿又画出各种草图,可忙乎了老半天都没有个结果。这时候爱迪生走过来,一看这情形笑了“何必这么麻烦呢,你把这只灯泡装满水,再把水倒入量杯中,灯泡的容积不就转化成水的体积被测量出来了吗?”听了这番话,助手恍然大悟,于是他依照这个办法,很快就把灯泡的容积测量出来了。
提问:
⑴
听了这则故事以后,你知道大发明家爱迪生是如何测出梨形灯泡的容积的吗?他有没有实际去测灯泡的容积?
⑵
他去测了什么?
⑶
爱迪生要测的是灯泡的容积,为什么变成了测水的体积呢?
⑷
爱迪生实际上是运用了一种策略,你知道是什么策略吗?
