2.5.1 一元一次不等式与一次函数 课件(共21张PPT)
文档属性
| 名称 | 2.5.1 一元一次不等式与一次函数 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 14:33:41 | ||
图片预览






文档简介
第5节 一元一次不等式与一次函数
(第1课时)
第二章 一元一次不等式和一元一次不等式组
2021年春北师大版八年级数学下册
1 会利用函数图象解一元一次不等式.(重点)
2 了解一元一次不等式与一次函数的关系.(难点)
学习目标
1 什么是一次函数?
如果两个变量x,y间的关系式可以表示成y = kx+b(k,b是常数,且k≠0),那么 y 就叫做 x 的一次函数.
新课导入
一元一次不等式与一次函数的关系
我们知道,一次函数的图象是一条直线.
解:
列表
x
y
0
–5
2.5
0
描点
连线
请画出一次函数 y=2x - 5的图象
1
2
3
4
-1
-1
-2
-3
-4
-5
1
2
3
O
x
y
y = 2x - 5
探究新知
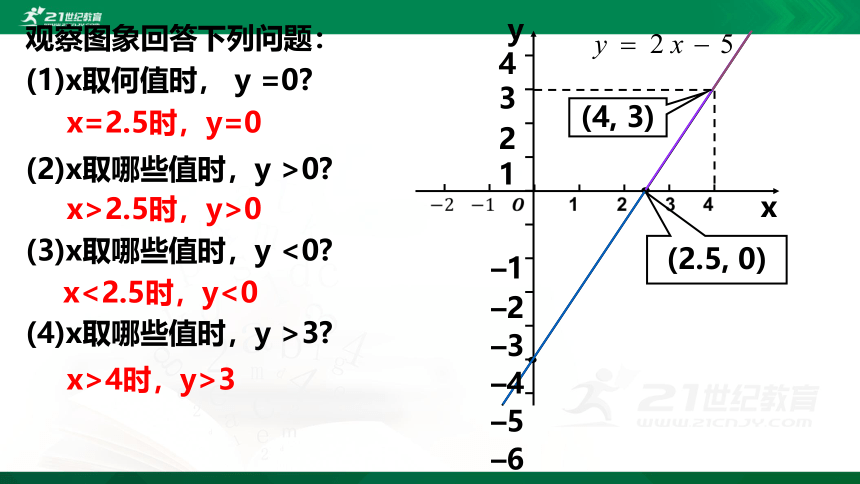
观察图象回答下列问题:
y
x
(1)x取何值时, y =0?
(2)x取哪些值时,y >0?
x=2.5时,y=0
(2.5, 0)
x>2.5时,y>0
(3)x取哪些值时,y <0?
(4)x取哪些值时,y >3?
x<2.5时,y<0
x>4时,y>3
(4, 3)
4
3
2
1
–1
–2
–3
–4
–5
–6
?
?
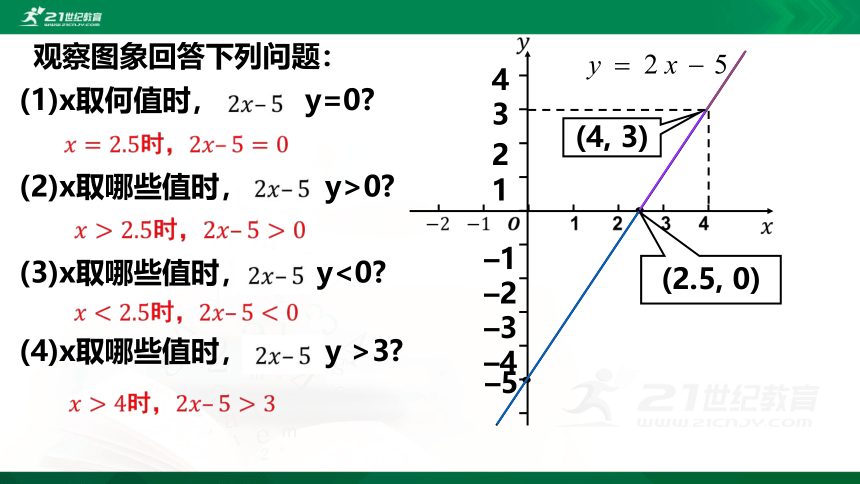
观察图象回答下列问题:
?
4
3
2
1
–1
–2
–3
–4
(1)x取何值时, y=0?
(2)x取哪些值时, y>0?
?
(2.5, 0)
?
(3)x取哪些值时, y<0?
(4)x取哪些值时, y >3?
?
?
(4, 3)
–5
1 一次函数和一元一次不等式的联系:
任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0,a,b为常数)的形式,所以解一元一次不等式可以看成是求一次函数y=ax+b(a≠0,a,b为常数)的函数值大于0或小于0时,自变量x的取值范围;反映在图象上,就是直线y=ax+b在x轴上方的部分或在x轴下方的部分对应的自变量x的取值范围.
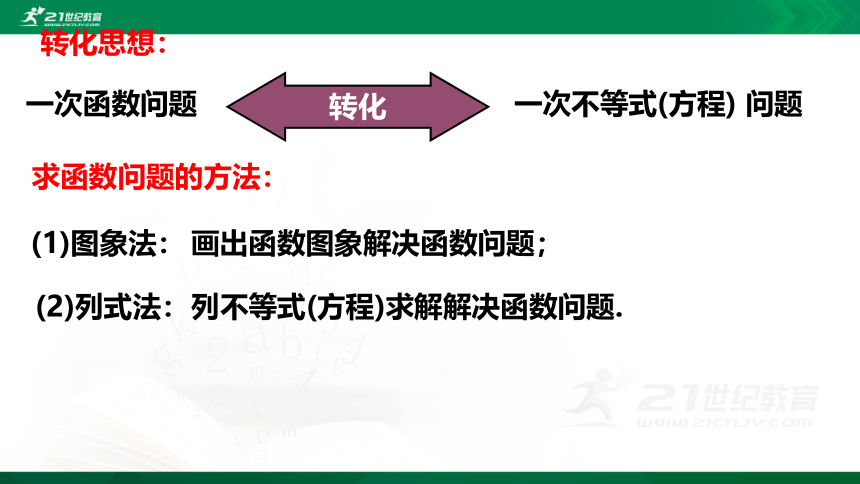
转化思想:
一次函数问题
一次不等式(方程) 问题
转化
求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式(方程)求解解决函数问题.
例1
方法一:代数法.
(1)y1>y2,即2x-5>3-2x,解得x>2.
(2)y1=y2,即2x-5=3-2x,解得x=2.
(3)y1<y2,即2x-5<3-2x,解得x<2.
所以当x>2时,y1>y2;当x=2时,y1=y2;
当x<2时,y1<y2.
解:
已知函数y1=2x-5,y2=3-2x,求当x取何值时,
(1) y1>y2? (2) y1=y2? (3) y1<y2?
例题讲解
方法二:图象法.
在同一直角坐标系内画出函数y1=2x-5和y2=3-2x的图象,如图所示.
由图象知,两直线的交点坐标为(2,-1).
观察图象可知,
当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2.
例2 兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,画出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20 m?谁先跑过100 m?
你是怎样求解的?与同伴交流.
例题讲解
解:设哥哥跑的时间为x秒,哥哥跑过的路程为y1 m,弟弟跑过的路程为y2 m,根据题意,得 y1=4x,y2=3x+9,
你感觉解决此问题的关键是什么?
作出一次函数图像,确定两个函数的交点坐标.
从图象上来看:
9 s时哥哥追上弟弟;
(1)当0 < x < 9时,弟弟跑在哥哥前面;
(2)当x > 9时,哥哥跑在弟弟前面;
(3)弟弟先跑过20 m,哥哥先跑过100 m;
例3 已知 y1 = -x + 3,y2 = 3x - 4 ,当 x 为何值时,y1 < y2 ?你是怎样做的?与同伴交流.
解:当y1 < y2 ,即-x + 3 < 3x-4时,x > ,所以当x > 时,y1 < y2 .
本题还可以画出y1 = -x + 3与y2 = 3x - 4 的图象,再利用图象进行比较说明.
例题讲解
利用图象法解不等式步骤:
(1)作出不等式左、右两边所对应的两个一次函数的图象.
(2)确定两个一次函数图象的交点坐标.
(3)找出哪段函数图象在上方,哪段函数在下方,从而确定自变量的取值范围.
1 直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( ) A.x≤3 B.x≥3
C.x≥-3 D.x≤0
课堂练习
2 一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
A.x≥2 B.x≤2 C.x≥4 D.x≤4
3 一次函数y=2x-4的图象与x轴的交点坐标为(2,0),则一元一次不等式2x-4≤0的解集为 ( )
A.x≤2 B.x<2 C.x≥2 D.x>2
4 已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x________时,y≤0.
5 已知一次函数y=kx+3的图象经过点(1,4).
(1)求这个一次函数的解析式;
(2)求关于x的不等式kx+3≤6的解集.
1 转化思想:
一次函数问题
一次不等式问题
转化
2 求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式求解集解决函数问题。
课堂小结
谢谢聆听
https://www.21cnjy.com/help/help_extract.php
(第1课时)
第二章 一元一次不等式和一元一次不等式组
2021年春北师大版八年级数学下册
1 会利用函数图象解一元一次不等式.(重点)
2 了解一元一次不等式与一次函数的关系.(难点)
学习目标
1 什么是一次函数?
如果两个变量x,y间的关系式可以表示成y = kx+b(k,b是常数,且k≠0),那么 y 就叫做 x 的一次函数.
新课导入
一元一次不等式与一次函数的关系
我们知道,一次函数的图象是一条直线.
解:
列表
x
y
0
–5
2.5
0
描点
连线
请画出一次函数 y=2x - 5的图象
1
2
3
4
-1
-1
-2
-3
-4
-5
1
2
3
O
x
y
y = 2x - 5
探究新知
观察图象回答下列问题:
y
x
(1)x取何值时, y =0?
(2)x取哪些值时,y >0?
x=2.5时,y=0
(2.5, 0)
x>2.5时,y>0
(3)x取哪些值时,y <0?
(4)x取哪些值时,y >3?
x<2.5时,y<0
x>4时,y>3
(4, 3)
4
3
2
1
–1
–2
–3
–4
–5
–6
?
?
观察图象回答下列问题:
?
4
3
2
1
–1
–2
–3
–4
(1)x取何值时, y=0?
(2)x取哪些值时, y>0?
?
(2.5, 0)
?
(3)x取哪些值时, y<0?
(4)x取哪些值时, y >3?
?
?
(4, 3)
–5
1 一次函数和一元一次不等式的联系:
任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0,a,b为常数)的形式,所以解一元一次不等式可以看成是求一次函数y=ax+b(a≠0,a,b为常数)的函数值大于0或小于0时,自变量x的取值范围;反映在图象上,就是直线y=ax+b在x轴上方的部分或在x轴下方的部分对应的自变量x的取值范围.
转化思想:
一次函数问题
一次不等式(方程) 问题
转化
求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式(方程)求解解决函数问题.
例1
方法一:代数法.
(1)y1>y2,即2x-5>3-2x,解得x>2.
(2)y1=y2,即2x-5=3-2x,解得x=2.
(3)y1<y2,即2x-5<3-2x,解得x<2.
所以当x>2时,y1>y2;当x=2时,y1=y2;
当x<2时,y1<y2.
解:
已知函数y1=2x-5,y2=3-2x,求当x取何值时,
(1) y1>y2? (2) y1=y2? (3) y1<y2?
例题讲解
方法二:图象法.
在同一直角坐标系内画出函数y1=2x-5和y2=3-2x的图象,如图所示.
由图象知,两直线的交点坐标为(2,-1).
观察图象可知,
当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2.
例2 兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,画出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20 m?谁先跑过100 m?
你是怎样求解的?与同伴交流.
例题讲解
解:设哥哥跑的时间为x秒,哥哥跑过的路程为y1 m,弟弟跑过的路程为y2 m,根据题意,得 y1=4x,y2=3x+9,
你感觉解决此问题的关键是什么?
作出一次函数图像,确定两个函数的交点坐标.
从图象上来看:
9 s时哥哥追上弟弟;
(1)当0 < x < 9时,弟弟跑在哥哥前面;
(2)当x > 9时,哥哥跑在弟弟前面;
(3)弟弟先跑过20 m,哥哥先跑过100 m;
例3 已知 y1 = -x + 3,y2 = 3x - 4 ,当 x 为何值时,y1 < y2 ?你是怎样做的?与同伴交流.
解:当y1 < y2 ,即-x + 3 < 3x-4时,x > ,所以当x > 时,y1 < y2 .
本题还可以画出y1 = -x + 3与y2 = 3x - 4 的图象,再利用图象进行比较说明.
例题讲解
利用图象法解不等式步骤:
(1)作出不等式左、右两边所对应的两个一次函数的图象.
(2)确定两个一次函数图象的交点坐标.
(3)找出哪段函数图象在上方,哪段函数在下方,从而确定自变量的取值范围.
1 直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( ) A.x≤3 B.x≥3
C.x≥-3 D.x≤0
课堂练习
2 一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
A.x≥2 B.x≤2 C.x≥4 D.x≤4
3 一次函数y=2x-4的图象与x轴的交点坐标为(2,0),则一元一次不等式2x-4≤0的解集为 ( )
A.x≤2 B.x<2 C.x≥2 D.x>2
4 已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x________时,y≤0.
5 已知一次函数y=kx+3的图象经过点(1,4).
(1)求这个一次函数的解析式;
(2)求关于x的不等式kx+3≤6的解集.
1 转化思想:
一次函数问题
一次不等式问题
转化
2 求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式求解集解决函数问题。
课堂小结
谢谢聆听
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
