五年级数学下册课件 - 7解决问题的策略 - 苏教版(共59张PPT)
文档属性
| 名称 | 五年级数学下册课件 - 7解决问题的策略 - 苏教版(共59张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 14:07:18 | ||
图片预览




文档简介
(共59张PPT)
解决问题的策略—转化
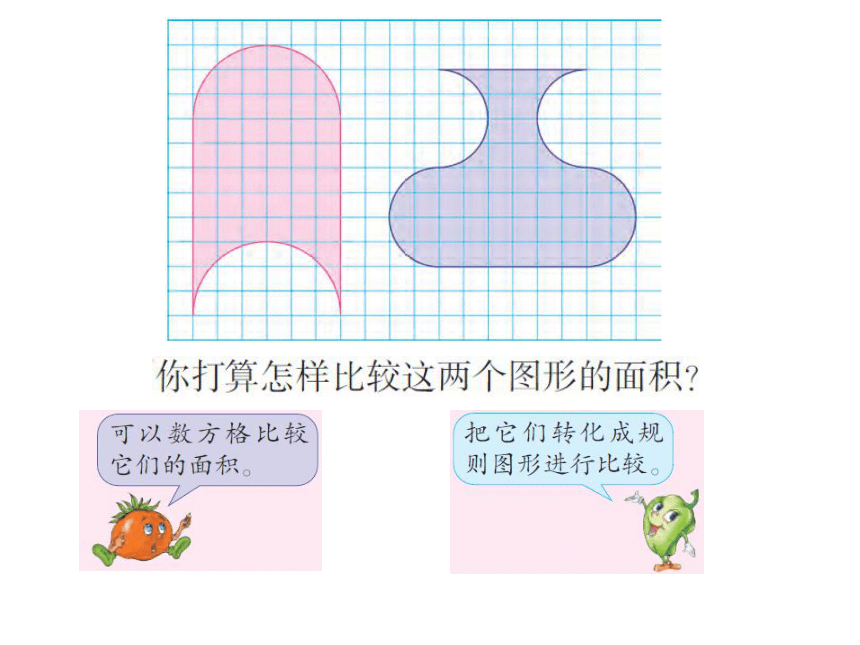
大象体重
同等石头的重量
转化
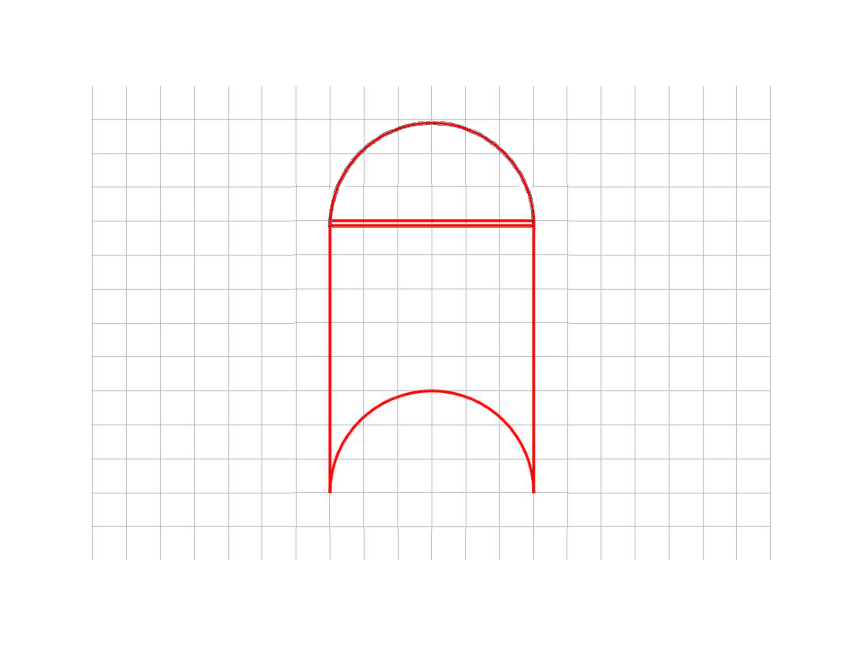
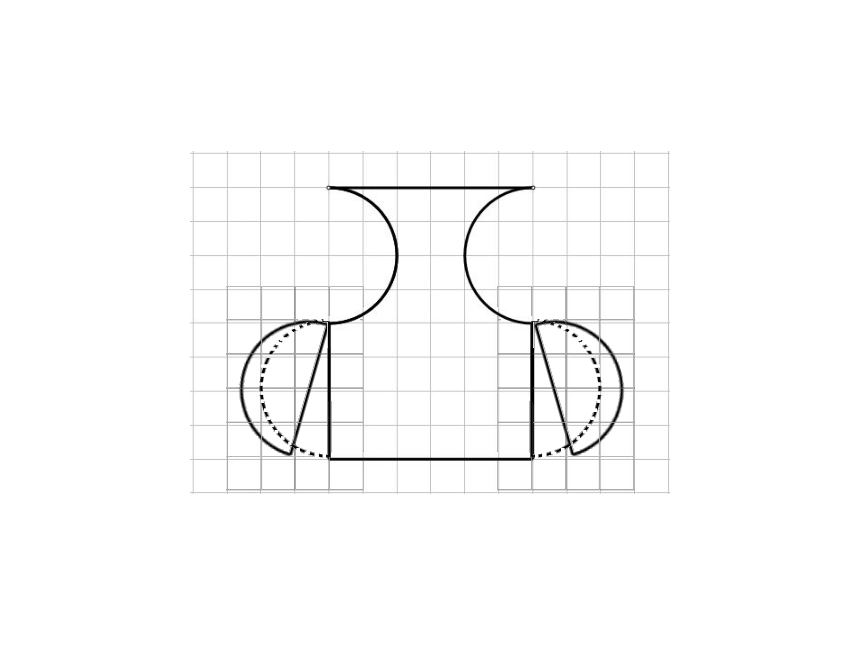
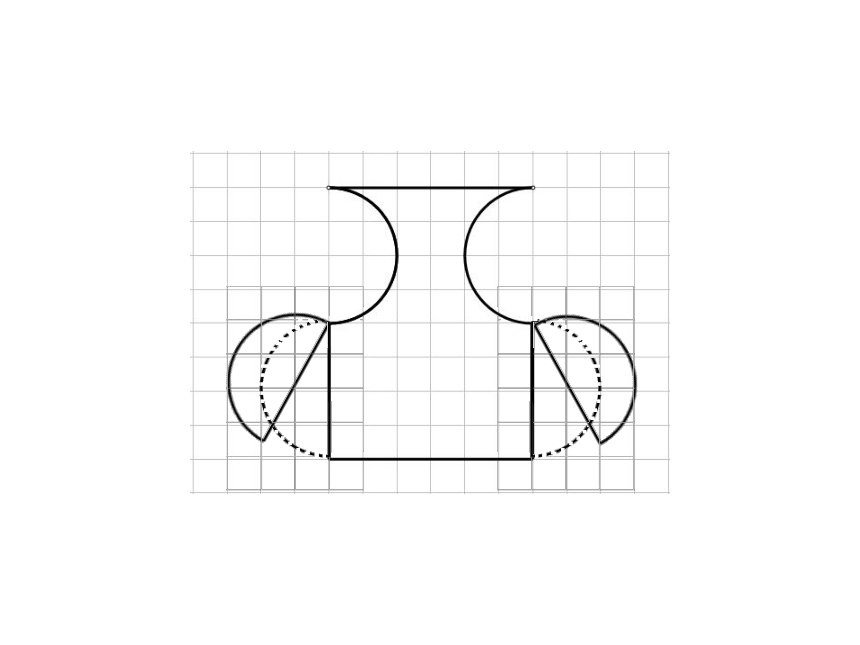
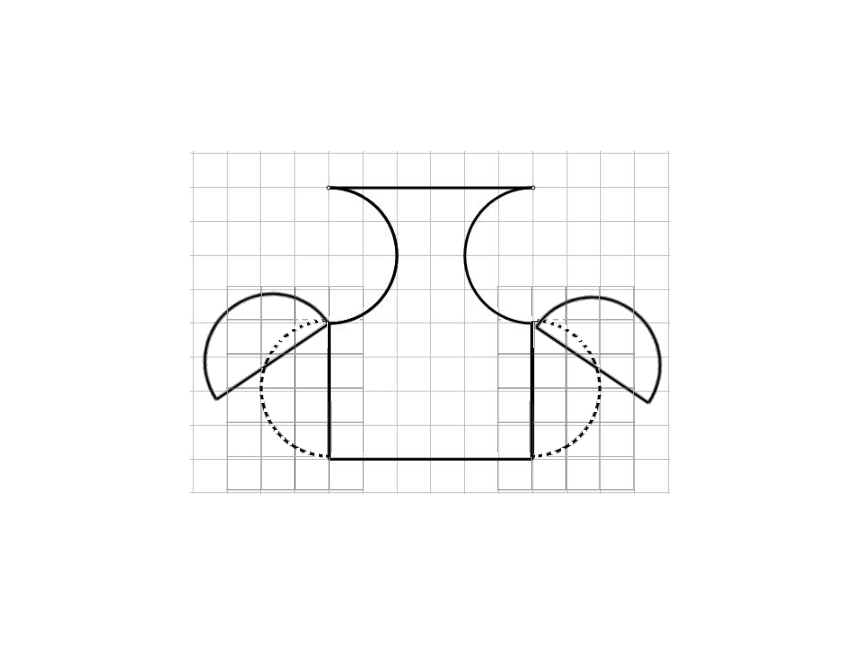
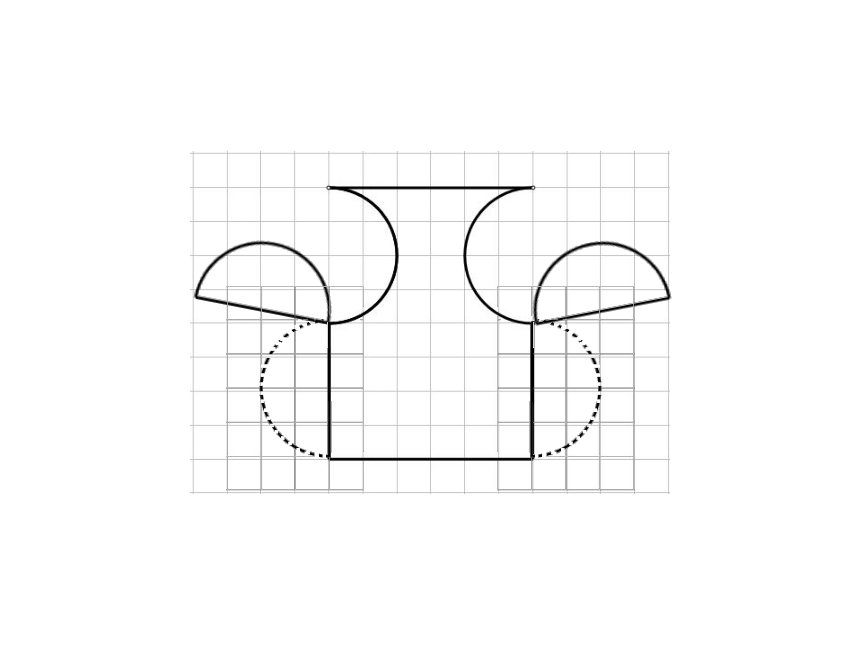
先把图形经过切割分成上、下两部分,
然后把切割后图形的上半部分(半圆)向下平移8格补在切割后图形的下半部分,使原图形转化为长方形。
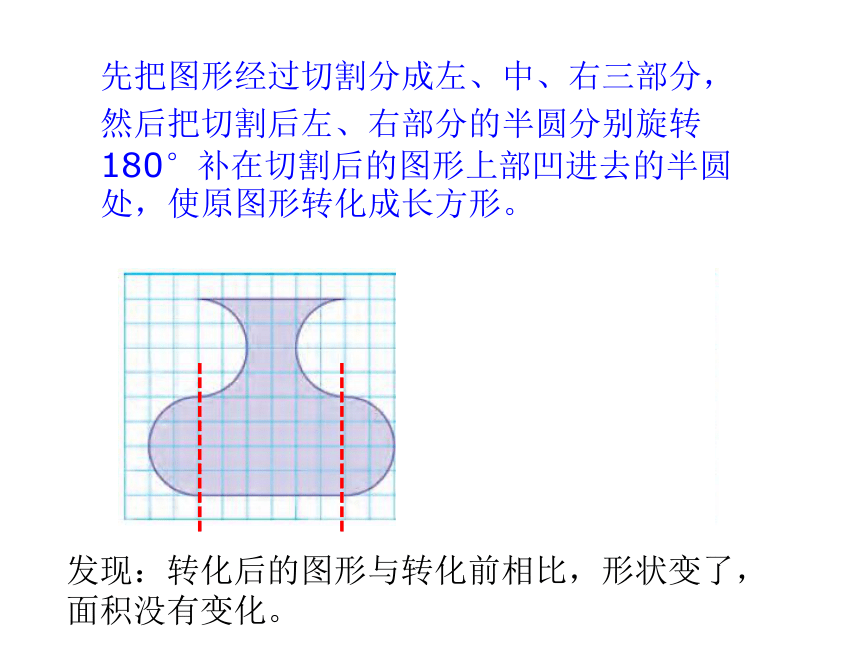
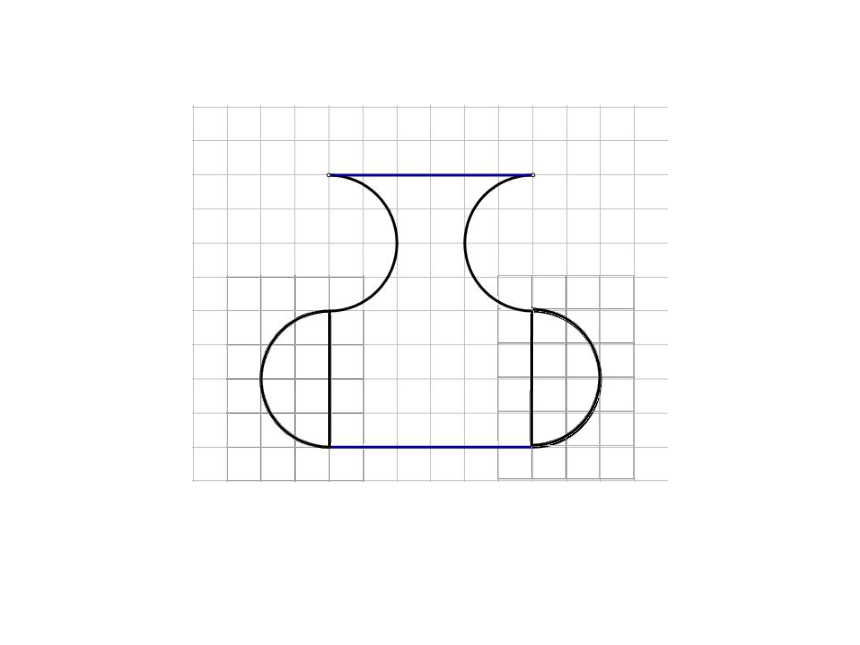
先把图形经过切割分成左、中、右三部分,
然后把切割后左、右部分的半圆分别旋转180°补在切割后的图形上部凹进去的半圆处,使原图形转化成长方形。
发现:转化后的图形与转化前相比,形状变了,面积没有变化。
由图可知,转化后这两个长方形的长都是8个小格,宽都是6个小格,所以这两个长方形面积相等,即原来两个图形面积相等。
1、解决例1提出的问题,我们应用了什么策略?
平移,旋转
2、用什么方法把不规则图形转化成规则图形?
转化
3、转化后的图形和转化前比,什么变了?什么没变?
形状变了,大小没变
以前研究平面图形和立体图形时,哪些地方也用到了转化的策略?
推导平行四边形的面积公式时,把平行四边形转化成长方形。
推导三角形的面积公式时,把三角形转化成平行四边形。
推导梯形的面积公式时,把梯形转化成平行四边形。
推导圆的面积时,把圆转化成长方形。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9
10
11
12
13
14
15
16
计算异分母分数加减法时,把异分母分数转化成同分母分数。
小数乘法可以先转化成整数计算
简便计算中算式的转化
8×
0.3
+
8×0.7
=8×(0.3
+0.7)
=8×1
=8
3-0.2
-0.8
=3
-(0.2+0.8)
=3
-1
=2
理一理:
1、平行四边形→长方形;
三角形、梯形→
平行四边形;
圆→长方形;
2、异分母分数加减法→同分母分数加减法;
3、简便计算中用过的式的转化
(化繁为简、化难为易,化陌生的新知为熟悉的旧知)
说一说:这样的转化有什么共同的地方?
形的转化
计算中
“数”的转化
江苏省电化教育馆制作
1
2
计算
+
+
+
1
4
1
16
1
8
江苏省电化教育馆制作
1
2
计算
+
+
+
1
4
1
16
1
8
1
2
1
4
1
8
1
16
江苏省电化教育馆制作
1
2
+
+
+
1
4
1
16
1
8
1
2
1
4
1
8
1
16
=1-
=
1
16
15
16
江苏省电化教育馆制作
1
2
+
+
+
+
1
4
1
16
1
8
1
2
1
4
1
8
1
16
1
32
=
?
这两个图案的面积相等。
因为第二个图案可以通过第一个图案平移得到,平移后长直条和短直条的长和宽都没有变化。
观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm?
计算下面图形的周长
1m
1m
1×4=4(m)
返回
计算下面图形的周长
r=4m
O
计算下面图形的周长
r=4m
O
红:4×2×3.14÷2=12.56(m)
黑:3.14×4=12.56(m)
计算下面图形的周长
r=4m
O
计算下面图形的周长
r=4m
O
用转化的策略解决问题
神奇化易是坦道,易化神奇不足提。
华罗庚
45-1×2=43(m)
27-1×2=25
(m)
43×25=1075(m2)
45-1×2=43(m)
27-1×2=25
(m)
43×25=1075(m2)
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
2
2.用分数表示图中的涂色部分。
(
)
(
)
1
2
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
5
8
通过这节课的学习,你有什么收获?
如果一件事物经过一番变化,已经知道了结果,要求原来的数量,那么我们就可以从这个结果开始倒推,运用“倒过来推想”的策略进行解题。
在倒过来推想的时候要注意变化顺序和变化方式。
解决问题的策略—转化
大象体重
同等石头的重量
转化
先把图形经过切割分成上、下两部分,
然后把切割后图形的上半部分(半圆)向下平移8格补在切割后图形的下半部分,使原图形转化为长方形。
先把图形经过切割分成左、中、右三部分,
然后把切割后左、右部分的半圆分别旋转180°补在切割后的图形上部凹进去的半圆处,使原图形转化成长方形。
发现:转化后的图形与转化前相比,形状变了,面积没有变化。
由图可知,转化后这两个长方形的长都是8个小格,宽都是6个小格,所以这两个长方形面积相等,即原来两个图形面积相等。
1、解决例1提出的问题,我们应用了什么策略?
平移,旋转
2、用什么方法把不规则图形转化成规则图形?
转化
3、转化后的图形和转化前比,什么变了?什么没变?
形状变了,大小没变
以前研究平面图形和立体图形时,哪些地方也用到了转化的策略?
推导平行四边形的面积公式时,把平行四边形转化成长方形。
推导三角形的面积公式时,把三角形转化成平行四边形。
推导梯形的面积公式时,把梯形转化成平行四边形。
推导圆的面积时,把圆转化成长方形。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9
10
11
12
13
14
15
16
计算异分母分数加减法时,把异分母分数转化成同分母分数。
小数乘法可以先转化成整数计算
简便计算中算式的转化
8×
0.3
+
8×0.7
=8×(0.3
+0.7)
=8×1
=8
3-0.2
-0.8
=3
-(0.2+0.8)
=3
-1
=2
理一理:
1、平行四边形→长方形;
三角形、梯形→
平行四边形;
圆→长方形;
2、异分母分数加减法→同分母分数加减法;
3、简便计算中用过的式的转化
(化繁为简、化难为易,化陌生的新知为熟悉的旧知)
说一说:这样的转化有什么共同的地方?
形的转化
计算中
“数”的转化
江苏省电化教育馆制作
1
2
计算
+
+
+
1
4
1
16
1
8
江苏省电化教育馆制作
1
2
计算
+
+
+
1
4
1
16
1
8
1
2
1
4
1
8
1
16
江苏省电化教育馆制作
1
2
+
+
+
1
4
1
16
1
8
1
2
1
4
1
8
1
16
=1-
=
1
16
15
16
江苏省电化教育馆制作
1
2
+
+
+
+
1
4
1
16
1
8
1
2
1
4
1
8
1
16
1
32
=
?
这两个图案的面积相等。
因为第二个图案可以通过第一个图案平移得到,平移后长直条和短直条的长和宽都没有变化。
观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm?
计算下面图形的周长
1m
1m
1×4=4(m)
返回
计算下面图形的周长
r=4m
O
计算下面图形的周长
r=4m
O
红:4×2×3.14÷2=12.56(m)
黑:3.14×4=12.56(m)
计算下面图形的周长
r=4m
O
计算下面图形的周长
r=4m
O
用转化的策略解决问题
神奇化易是坦道,易化神奇不足提。
华罗庚
45-1×2=43(m)
27-1×2=25
(m)
43×25=1075(m2)
45-1×2=43(m)
27-1×2=25
(m)
43×25=1075(m2)
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
4
2.用分数表示图中的涂色部分。
(
)
(
)
1
2
2.用分数表示图中的涂色部分。
(
)
(
)
1
2
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
2.用分数表示图中的涂色部分。
(
)
(
)
5
8
通过这节课的学习,你有什么收获?
如果一件事物经过一番变化,已经知道了结果,要求原来的数量,那么我们就可以从这个结果开始倒推,运用“倒过来推想”的策略进行解题。
在倒过来推想的时候要注意变化顺序和变化方式。
