2.4.1 一元一次不等式 课件(共23张PPT)
文档属性
| 名称 | 2.4.1 一元一次不等式 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览








文档简介
第4节 一元一次不等式
(第1课时)
第二章 一元一次不等式和一元一次不等式组
2021年春北师大版八年级数学下册
1 知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上。(重点)
2 通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤。(难点)
学习目标
不等式的基本性质
不等式的基本性质2:不等式两边同时乘以(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3:不等式两边同时乘以(或除以)同一个负数,不等号的方向改变.
不等式的基本性质1:不等式两边同时加上(或减去)同一个整式,不等号的方向不变.
新课导入
运用不等式基本性质把下列不等式化成 x > a或 x < a的形式.
①x - 4 < 6 ②2x > x - 5
③ x – 4 < 6 ④ x ≥ + x
解:① x < 10 ② x > - 5
③ x < 30 ④ x ≤ -
什么是不等式的解集?
一个含有未知数的不等式的所有解,组成这个不等式的解集.
什么叫一元一次方程?解一元一次方程的步骤是什么?
只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.
一元一次不等式
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点?
一元一次不等式
1 只有一个未知数
2 未知数的指数是一次
3 不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
探究新知
一元一次不等式的定义:
只含有一个未知数,并且未知数的最高次数1,像这样的不等式,叫做一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
例1 下列式子中是一元一次不等式的有( )
(1)x2+1>2x; (2) +2>0;
(3)x>y; (4) ≤1.
A.1个 B.2个 C.3个 D.4个
A
例题讲解
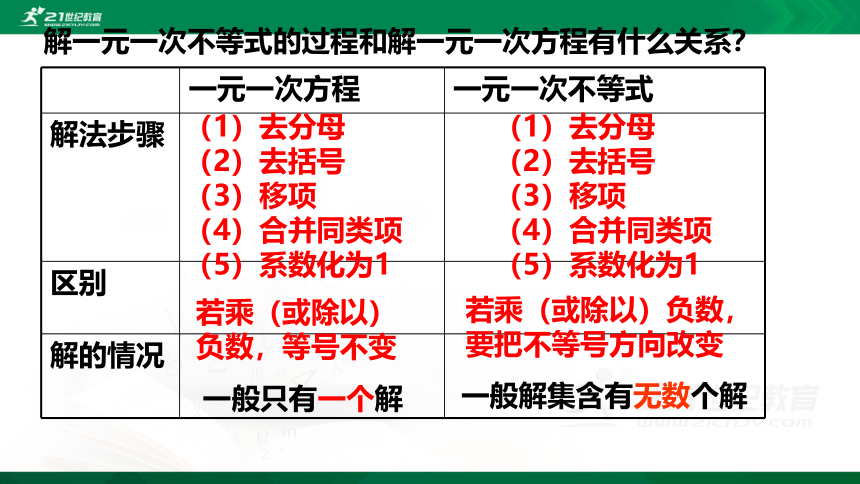
解一元一次不等式的过程和解一元一次方程有什么关系?
一元一次方程
一元一次不等式
解法步骤
区别
解的情况
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
若乘(或除以)负数,要把不等号方向改变
一般解集含有无数个解
若乘(或除以)负数,等号不变
一般只有一个解
解一元一次不等式
解一元一次不等式的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.
探究新知
例2 解不等式 3 - x < 2x + 6,并把它的解集表示在数轴上.
解:两边都加 -2x,得 3 - x - 2x < 2x + 6 - 2x.
合并同类项,得 3 - 3x < 6.
两边都加-3,得 3- 3x - 3 < 6 - 3.
合并同类项,得 -3x < 3.
两边都除以-3,得 x > -1.
例题讲解
0
1
2
-1
-2
这个不等式的解集在数轴上的表示如图所示:
例3 解不等式 ,并把解集在数轴上表示出来.
解:去分母,得14x-7(3x-8)+14≥4(10-x).
去括号,得14x-21x+56+14≥40-4x.
移项,得14x-21x+4x≥40-56-14.
合并同类项,得-3x≥-30.
系数化为1,得x≤10.
这个不等式的解集在数轴上的表示如图所示.
例题讲解
一元一次不等式的特殊解
例4
求不等式3(x+1)≥5x-9的非负整数解.
解不等式3(x+1)≥5x-9得x≤6,
∴不等式3(x+1)≥5x-9的非负整数解为
0,1,2,3,4,5,6.
探究新知
1 下列不等式中,是一元一次不等式的是( )
B.a2+b2>0
C. >1 D.x<y
课堂练习
2 解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
3 不等式4-2x>0的解集在数轴上表示为( )
4 若关于x的一元一次方程x-m+2=0的解是负数,则m的取值范围是( )
A.m≥2 B.m>2
C.m<2 D.m≤2
5 当自然数k=__________时,关于x的方程 x-3k=5(x-k)+6的解是负数.
6 若2(x+1)-5<3(x-1)+4的最小整数解是方程
x-mx=5的解,求 的值.
解一元一次不等式的一般步骤
(1)去分母———不等式性质2或3
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,须注意不等号的方向要改变.
(2)去括号——去括号法则和分配律
注意:①勿漏乘括号内每一项;②括号前面是“-”号,括号内各项要变号.
课堂小结
(3)移项——移项法则(不等式性质1)
注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)把系数化成1——不等式基本性质2或性质3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
谢谢聆听
https://www.21cnjy.com/help/help_extract.php
(第1课时)
第二章 一元一次不等式和一元一次不等式组
2021年春北师大版八年级数学下册
1 知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上。(重点)
2 通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤。(难点)
学习目标
不等式的基本性质
不等式的基本性质2:不等式两边同时乘以(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3:不等式两边同时乘以(或除以)同一个负数,不等号的方向改变.
不等式的基本性质1:不等式两边同时加上(或减去)同一个整式,不等号的方向不变.
新课导入
运用不等式基本性质把下列不等式化成 x > a或 x < a的形式.
①x - 4 < 6 ②2x > x - 5
③ x – 4 < 6 ④ x ≥ + x
解:① x < 10 ② x > - 5
③ x < 30 ④ x ≤ -
什么是不等式的解集?
一个含有未知数的不等式的所有解,组成这个不等式的解集.
什么叫一元一次方程?解一元一次方程的步骤是什么?
只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.
一元一次不等式
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点?
一元一次不等式
1 只有一个未知数
2 未知数的指数是一次
3 不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
探究新知
一元一次不等式的定义:
只含有一个未知数,并且未知数的最高次数1,像这样的不等式,叫做一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
例1 下列式子中是一元一次不等式的有( )
(1)x2+1>2x; (2) +2>0;
(3)x>y; (4) ≤1.
A.1个 B.2个 C.3个 D.4个
A
例题讲解
解一元一次不等式的过程和解一元一次方程有什么关系?
一元一次方程
一元一次不等式
解法步骤
区别
解的情况
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
若乘(或除以)负数,要把不等号方向改变
一般解集含有无数个解
若乘(或除以)负数,等号不变
一般只有一个解
解一元一次不等式
解一元一次不等式的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.
探究新知
例2 解不等式 3 - x < 2x + 6,并把它的解集表示在数轴上.
解:两边都加 -2x,得 3 - x - 2x < 2x + 6 - 2x.
合并同类项,得 3 - 3x < 6.
两边都加-3,得 3- 3x - 3 < 6 - 3.
合并同类项,得 -3x < 3.
两边都除以-3,得 x > -1.
例题讲解
0
1
2
-1
-2
这个不等式的解集在数轴上的表示如图所示:
例3 解不等式 ,并把解集在数轴上表示出来.
解:去分母,得14x-7(3x-8)+14≥4(10-x).
去括号,得14x-21x+56+14≥40-4x.
移项,得14x-21x+4x≥40-56-14.
合并同类项,得-3x≥-30.
系数化为1,得x≤10.
这个不等式的解集在数轴上的表示如图所示.
例题讲解
一元一次不等式的特殊解
例4
求不等式3(x+1)≥5x-9的非负整数解.
解不等式3(x+1)≥5x-9得x≤6,
∴不等式3(x+1)≥5x-9的非负整数解为
0,1,2,3,4,5,6.
探究新知
1 下列不等式中,是一元一次不等式的是( )
B.a2+b2>0
C. >1 D.x<y
课堂练习
2 解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
3 不等式4-2x>0的解集在数轴上表示为( )
4 若关于x的一元一次方程x-m+2=0的解是负数,则m的取值范围是( )
A.m≥2 B.m>2
C.m<2 D.m≤2
5 当自然数k=__________时,关于x的方程 x-3k=5(x-k)+6的解是负数.
6 若2(x+1)-5<3(x-1)+4的最小整数解是方程
x-mx=5的解,求 的值.
解一元一次不等式的一般步骤
(1)去分母———不等式性质2或3
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,须注意不等号的方向要改变.
(2)去括号——去括号法则和分配律
注意:①勿漏乘括号内每一项;②括号前面是“-”号,括号内各项要变号.
课堂小结
(3)移项——移项法则(不等式性质1)
注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)把系数化成1——不等式基本性质2或性质3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
谢谢聆听
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
