2020-2021学年沪科版九年级下学期数学强化训练题一(word版含答案)
文档属性
| 名称 | 2020-2021学年沪科版九年级下学期数学强化训练题一(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 345.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 19:04:08 | ||
图片预览




文档简介
2021沪科版数学强化训练题一
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1.-3的绝对值是
(
)
A.-3
B.3
C.
D.-
2.疫情期间,高速免费79天,仅3月5日一天,高速免费惠及2650万辆车,累计减免通行费用达15亿元,将数字“15亿”用科学记数法表示为
(
)
A.2.65×107
B.265×104
C.1.5×109
D.
1.5×1010
3.在“美丽乡村”评选活动中,某乡镇7个村的得分为:86,98,90,88,96,92,96,这组数据的中位数和众数分别是(
)
A.92,96
B.90,96
C.92,98
D.92,92
4.式子在实数范围内有意义,则x的取值范围是(
)
A.x=0
B.x≥0
C.x>-4
D.x≥-4
5.下列计算正确的是
(
)
A.6a3-a3=5a3
B.a3·a3=a9
C.(3a)2=6a2
D.a6÷a2=a3
6.如果a>b,那么下列结论一定正确的是
(
)
A.a-3<b-3
B.3-a<3-b
C.ac>bc
D.a2>b2
7.方程3x2-2x-1=0的根的情况是
(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根
8.下列命题中,是假命题的是
(
)
A.两点确定一条直线
B.平行线之间的距离处处相等
C.角平分线上的点到这个角两边的距离相等
D.同位角相等
9.如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD=2,DB=3,AC=10,则AE等于
(
)
A.3
B.4
C.5
D.6
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图,A,B,C是⊙O上的三个点,∠AOB=58°,则∠BCA的度数是
(
)
A.58°
B.42°
C.32°
D.29°
11.如图,矩形ABCD的对角线AC,BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F.已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是
(
)
A.先增大,后减小
B.先减小,后增大
C.始终等于2.4
D.始终等于3
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是
(
)
A.①③ B.②④ C.①③④ D.②③④
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算
=
.
14.分解因式:a3+2a2+a=
.
15.疫情期间,某校有6名教师志愿者进行值班,其中4名女教师志愿者,2名男教师志愿者,若随机抽取2人为组长,恰好抽到2名男教师志愿者的概率为
.
16.如图,直线m∥n,∠1=70°,∠2=28°32′,
则∠A等于
.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA=6,则阴影部分的面积为
.
18.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,对称轴为直线x=1,则下列结论:①>0;
②a+b+c=0;
③关于x的方程ax2+bx+c+2=0无实根,④ac-b+1=0;⑤OA·OB=-.其中正确结论有
.
三、解答题(本大题共8小题,共66分)
19.(本题满分10分,每小题5分)
(1)计算:(-1)2
021-+2sin
30°+|-|
(2)解方程:+1=.
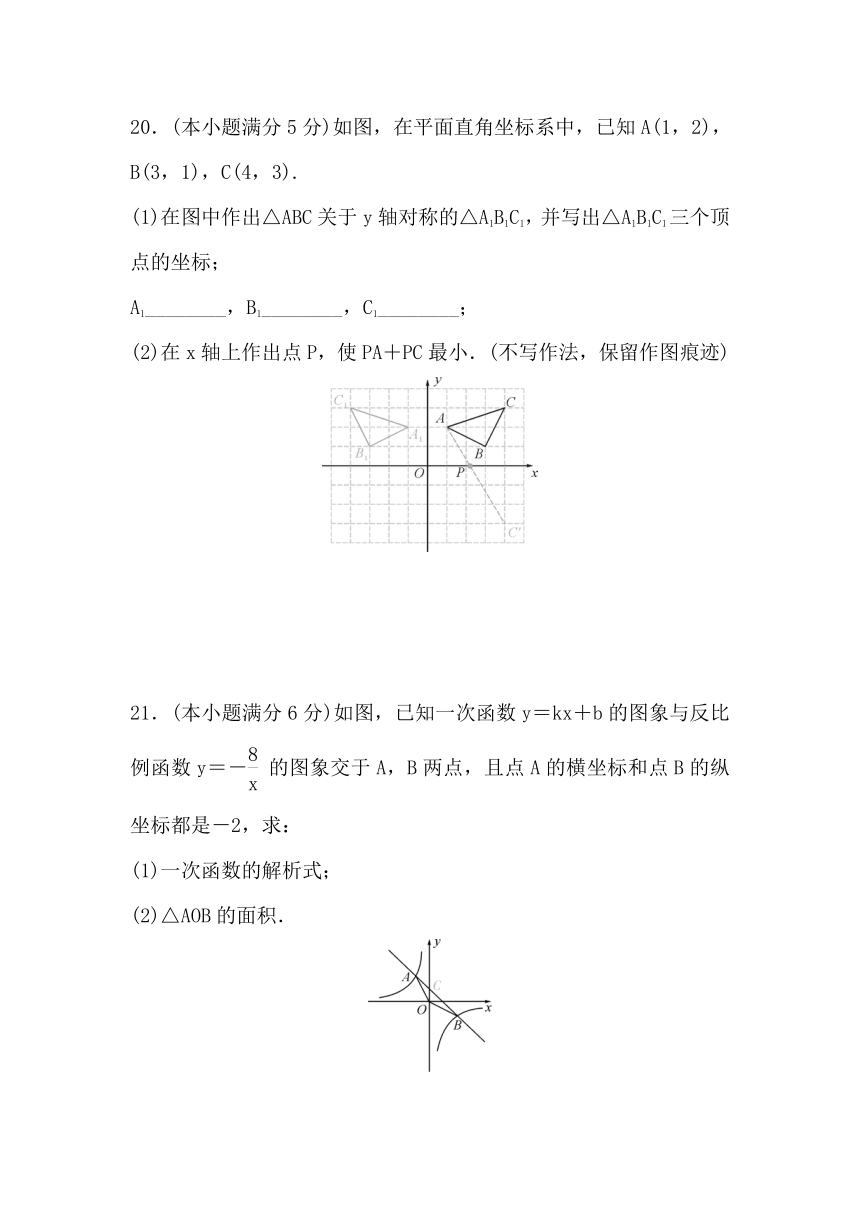
20.(本小题满分5分)如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(4,3).
(1)在图中作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
A1________,B1________,C1________;
(2)在x轴上作出点P,使PA+PC最小.(不写作法,保留作图痕迹)
21.(本小题满分6分)如图,已知一次函数y=kx+b的图象与反比例函数y=-的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
(1)一次函数的解析式;
(2)△AOB的面积.
22.(本小题满分8分)疫情过去复学后,某校为了了解学生对疫情防控知识的掌握情况,随机抽测了本校部分学生进行了测试,共10个题,并将测试得到的情况绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=____%,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是____个、____个.
(3)该校共有学生2
400人,如果答对题达6个以上(含6个)为合格,请你估计该校学生对疫情防控知识掌握合格的有多少名?
23.(本小题满分8分)(2020·百色模拟)高铁苏州北站已于几年前投入使用,计划在广场内种植A,B两种花木共10
500棵,若B花木数量是A花木数量的一半多1
500棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排27人同时种植这两种花木,每人每天能种植A花木50棵或B花木30棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
24.(本小题满分8分)(2020·贵港港南区一模)如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC,AB的长.
25.(本小题满分11分)(2020·贵港港南区一模)如图,已知抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0).
(1)求该抛物线的表达式;
(2)点E是线段BC上方的抛物线上一个动点,求△BEC的面积的最大值;
(3)点P是抛物线的对称轴上一个动点,当以A,P,C为顶点的三角形是直角三角形时,求出点P的坐标.
26.(本小题满分10分)在菱形ABCD中,∠ABC=60°,点P是对角线BD上一动点,将线段CP绕点C顺时针旋转120°到CQ,连接DQ.连接QP并延长,分别交AB,CD于点M,N.
(1)如图①,求证:△BCP≌△DCQ;
(2)如图②,已知PM=QN;若MN的最小值为2,求菱形ABCD的面积.
eq
\o(\s\up7(),\s\do5(图①))
eq
\o(\s\up7(),\s\do5(图②))
答案
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1.-3的绝对值是
(
B
)
A.-3
B.3
C.
D.-
2.疫情期间,高速免费79天,仅3月5日一天,高速免费惠及2650万辆车,累计减免通行费用达15亿元,将数字“15亿”用科学记数法表示为
(
C
)
A.2.65×107
B.265×104
C.1.5×109
D.
1.5×1010
3.在“美丽乡村”评选活动中,某乡镇7个村的得分为:86,98,90,88,96,92,96,这组数据的中位数和众数分别是(
A
)
A.92,96
B.90,96
C.92,98
D.92,92
4.式子在实数范围内有意义,则x的取值范围是(
D
)
A.x=0
B.x≥0
C.x>-4
D.x≥-4
5.下列计算正确的是
(
A
)
A.6a3-a3=5a3
B.a3·a3=a9
C.(3a)2=6a2
D.a6÷a2=a3
6.如果a>b,那么下列结论一定正确的是
(
B
)
A.a-3<b-3
B.3-a<3-b
C.ac>bc
D.a2>b2
7.方程3x2-2x-1=0的根的情况是
(
A
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根
8.下列命题中,是假命题的是
(
D
)
A.两点确定一条直线
B.平行线之间的距离处处相等
C.角平分线上的点到这个角两边的距离相等
D.同位角相等
9.如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD=2,DB=3,AC=10,则AE等于
(
B
)
A.3
B.4
C.5
D.6
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图,A,B,C是⊙O上的三个点,∠AOB=58°,则∠BCA的度数是
(
D
)
A.58°
B.42°
C.32°
D.29°
11.如图,矩形ABCD的对角线AC,BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F.已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是
(
C
)
A.先增大,后减小
B.先减小,后增大
C.始终等于2.4
D.始终等于3
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.★如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是
(
C
)
A.①③ B.②④ C.①③④ D.②③④
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算
=3.
14.分解因式:a3+2a2+a=a(a+1)2.
15.疫情期间,某校有6名教师志愿者进行值班,其中4名女教师志愿者,2名男教师志愿者,若随机抽取2人为组长,恰好抽到2名男教师志愿者的概率为.
17.如图,直线m∥n,∠1=70°,∠2=28°32′,
则∠A等于41°28′
.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA=6,则阴影部分的面积为3+3π
.
18.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,对称轴为直线x=1,则下列结论:①>0;
②a+b+c=0;
③关于x的方程ax2+bx+c+2=0无实根,④ac-b+1=0;⑤OA·OB=-.其中正确结论有④⑤.
三、解答题(本大题共8小题,共66分)
19.(本题满分10分,每小题5分)
(1)计算:(-1)2
021-+2sin
30°+|-|
解:原式=-1-2+1+2
=2-2.
(2)解方程:+1=.
解:方程两边同乘(x-2)得
x-3+x-2=-3
解得x=1,
检验:当x=1时,x-2≠0,故x=1是此分式方程的解.
20.(本小题满分5分)如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(4,3).
(1)在图中作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
A1________,B1________,C1________;
(2)在x轴上作出点P,使PA+PC最小.(不写作法,保留作图痕迹)
解:(1)如图所示,△A1B1C1即为所求,
A1(-1,2),B1
(-3,1),C1
(-4,3);
故答案为(-1,2),(-3,1),(-4,3);
(2)如图所示,点P即为所求.
21.(本小题满分6分)如图,已知一次函数y=kx+b的图象与反比例函数y=-的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
(1)一次函数的解析式;
(2)△AOB的面积.
解:(1)由题意A(-2,4),B(4,-2),
∵一次函数过A,B两点,
∴解得
∴一次函数的解析式为y=-x+2;
(2)设直线AB与y轴交于C,则C(0,2),
∵S△AOC=×OC×|xA|,S△BOC=×OC×|xB|
∴S△AOB=S△AOC+S△BOC=·OC·|xA|+·OC·|xB|
=×2×2+×2×4=6.
22.(本小题满分8分)疫情过去复学后,某校为了了解学生对疫情防控知识的掌握情况,随机抽测了本校部分学生进行了测试,共10个题,并将测试得到的情况绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=____%,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是____个、____个.
(3)该校共有学生2
400人,如果答对题达6个以上(含6个)为合格,请你估计该校学生对疫情防控知识掌握合格的有多少名?
解:(1)扇形统计图中a=1-30%-15%-10%-20%=25%,
设答对6个题的学生有x人,由题意得=,解得x=50.
补全条形统计图如图所示:
(2)
由条形图可知,答对5个题的学生有60人,人数最多,
所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,
故中位数为(5+5)÷2=5.
(3)×2
400=1
080(名).
答:估计该校对疫情防控知识掌握合格的同学有1
080名.
23.(本小题满分8分)(2020·百色模拟)高铁苏州北站已于几年前投入使用,计划在广场内种植A,B两种花木共10
500棵,若B花木数量是A花木数量的一半多1
500棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排27人同时种植这两种花木,每人每天能种植A花木50棵或B花木30棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
解:(1)设A花木的数量是x棵,B花木的数量是y棵,根据题意可得:解得
答:A花木的数量是6
000棵,B花木的数量是4
500棵;
(2)设安排a人种植A花木,则安排(27-a)人种植B花木,
=,
解得a=12,经检验,a=12是原方程的解,
∴27-a=15,
答:安排12人种植A花木,15人种植B花木,才能确保同时完成各自的任务.
24.(本小题满分8分)(2020·贵港港南区一模)如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC,AB的长.
(1)证明:连接OC.
∵点C在⊙O上,OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,∴∠DAC=∠OCA.
∵CD⊥PA,
∴∠CDA=90°,∴∠CAD+∠DCA=90°,
∴∠DCO=∠DCA+∠ACO=∠DCA+∠DAC=90°,
∵点C是⊙O上一点,
∴CD是⊙O切线.
(2)解:作OF⊥AB于F,
∴∠OCD=∠CDF=∠OFD=90°,
∴四边形CDFO是矩形,∴OC=FD,OF=CD,
∵CD=2AD,设AD=x,则OF=CD=2x,
∵DF=OC=10,
∴AF=10-x,
在Rt△AOF中,AF2+OF2=OA2,
∴(10-x)2+(2x)2=102,
解得x=4或0(舍去),
∴AD=4,AF=6,OF=CD+8.
∴AC==4,
∵OF⊥AB,
∴AB=2AF=2·=12.
25.(本小题满分11分)(2020·贵港港南区一模)如图,已知抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0).
(1)求该抛物线的表达式;
(2)点E是线段BC上方的抛物线上一个动点,求△BEC的面积的最大值;
(3)点P是抛物线的对称轴上一个动点,当以A,P,C为顶点的三角形是直角三角形时,求出点P的坐标.
解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0),
∴解得
∴y=-x2+2x+3=-(x-1)2+4;
(2)如解图,作EF∥y轴交BC于点F,记△BEC的面积为S,
∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3.
设E(m,-m2+2m+3)(0∴EF=(-m2+2m+3)-(-m+3)=-m2+3m.
解图
∴S=EF·OB=(-m2+3m)×3=-(m-)2+.
∵-<0,0∴当m=时,S最大=,
此时,点E的坐标是(,).
(3)
∵抛物线对称轴为直线x=1,∴可设P(1,n),
∵A(-1,0),C(0,3),
∴AC2=10,AP2=4+n2,CP2=1+(n-3)2=n2-6n+10.
①当AC⊥AP时,AC2+AP2=CP2,
即10+4+n2=n2-6n+10.
解得n=-;
②当AC⊥CP时,AC2+CP2=AP2,
即10+n2-6n+10=4+n2,
解得n=;
③当AP⊥CP时,AP2+CP2=AC2,
即4+n2+n2-6n+10=10.
解得n=1或2.
综上所述,符合条件的点P的坐标是(1,-)或(1,)或(1,1)或(1,2).
26.(本小题满分10分)在菱形ABCD中,∠ABC=60°,点P是对角线BD上一动点,将线段CP绕点C顺时针旋转120°到CQ,连接DQ.连接QP并延长,分别交AB,CD于点M,N.
(1)如图①,求证:△BCP≌△DCQ;
(2)如图②,已知PM=QN;若MN的最小值为2,求菱形ABCD的面积.
eq
\o(\s\up7(),\s\do5(图①))
eq
\o(\s\up7(),\s\do5(图②))
(1)证明:∵四边形ABCD是菱形,
∴BC=DC,AB∥CD,
∴∠PBM=∠PBC=∠ABC=30°,∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=120°
由旋转的性质得PC=QC,∠PCQ=120°,
∴∠BCD=∠PCQ,即∠BCP+∠PCD=∠DCQ+∠PCD,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
∴△BCP≌△DCQ(SAS);
(2)解:过点C作CG⊥PQ于点G,连接AC,
∵PC=QC,∠PCQ=120°,
∴∠PCG=60°,PG=QG,∴PG=PC,∴PQ=PC.
∵PM=QN,
∴MN=PQ=PC,
∴当PC⊥BD时,PC最小,此时MN最小,
∴PC=2,在Rt△BPC中,BC=2PC=4,
∵菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴S△ABC=×4×2=4,
∴菱形ABCD的面积=2S△ABC=2×4=8.
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1.-3的绝对值是
(
)
A.-3
B.3
C.
D.-
2.疫情期间,高速免费79天,仅3月5日一天,高速免费惠及2650万辆车,累计减免通行费用达15亿元,将数字“15亿”用科学记数法表示为
(
)
A.2.65×107
B.265×104
C.1.5×109
D.
1.5×1010
3.在“美丽乡村”评选活动中,某乡镇7个村的得分为:86,98,90,88,96,92,96,这组数据的中位数和众数分别是(
)
A.92,96
B.90,96
C.92,98
D.92,92
4.式子在实数范围内有意义,则x的取值范围是(
)
A.x=0
B.x≥0
C.x>-4
D.x≥-4
5.下列计算正确的是
(
)
A.6a3-a3=5a3
B.a3·a3=a9
C.(3a)2=6a2
D.a6÷a2=a3
6.如果a>b,那么下列结论一定正确的是
(
)
A.a-3<b-3
B.3-a<3-b
C.ac>bc
D.a2>b2
7.方程3x2-2x-1=0的根的情况是
(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根
8.下列命题中,是假命题的是
(
)
A.两点确定一条直线
B.平行线之间的距离处处相等
C.角平分线上的点到这个角两边的距离相等
D.同位角相等
9.如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD=2,DB=3,AC=10,则AE等于
(
)
A.3
B.4
C.5
D.6
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图,A,B,C是⊙O上的三个点,∠AOB=58°,则∠BCA的度数是
(
)
A.58°
B.42°
C.32°
D.29°
11.如图,矩形ABCD的对角线AC,BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F.已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是
(
)
A.先增大,后减小
B.先减小,后增大
C.始终等于2.4
D.始终等于3
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是
(
)
A.①③ B.②④ C.①③④ D.②③④
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算
=
.
14.分解因式:a3+2a2+a=
.
15.疫情期间,某校有6名教师志愿者进行值班,其中4名女教师志愿者,2名男教师志愿者,若随机抽取2人为组长,恰好抽到2名男教师志愿者的概率为
.
16.如图,直线m∥n,∠1=70°,∠2=28°32′,
则∠A等于
.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA=6,则阴影部分的面积为
.
18.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,对称轴为直线x=1,则下列结论:①>0;
②a+b+c=0;
③关于x的方程ax2+bx+c+2=0无实根,④ac-b+1=0;⑤OA·OB=-.其中正确结论有
.
三、解答题(本大题共8小题,共66分)
19.(本题满分10分,每小题5分)
(1)计算:(-1)2
021-+2sin
30°+|-|
(2)解方程:+1=.
20.(本小题满分5分)如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(4,3).
(1)在图中作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
A1________,B1________,C1________;
(2)在x轴上作出点P,使PA+PC最小.(不写作法,保留作图痕迹)
21.(本小题满分6分)如图,已知一次函数y=kx+b的图象与反比例函数y=-的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
(1)一次函数的解析式;
(2)△AOB的面积.
22.(本小题满分8分)疫情过去复学后,某校为了了解学生对疫情防控知识的掌握情况,随机抽测了本校部分学生进行了测试,共10个题,并将测试得到的情况绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=____%,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是____个、____个.
(3)该校共有学生2
400人,如果答对题达6个以上(含6个)为合格,请你估计该校学生对疫情防控知识掌握合格的有多少名?
23.(本小题满分8分)(2020·百色模拟)高铁苏州北站已于几年前投入使用,计划在广场内种植A,B两种花木共10
500棵,若B花木数量是A花木数量的一半多1
500棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排27人同时种植这两种花木,每人每天能种植A花木50棵或B花木30棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
24.(本小题满分8分)(2020·贵港港南区一模)如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC,AB的长.
25.(本小题满分11分)(2020·贵港港南区一模)如图,已知抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0).
(1)求该抛物线的表达式;
(2)点E是线段BC上方的抛物线上一个动点,求△BEC的面积的最大值;
(3)点P是抛物线的对称轴上一个动点,当以A,P,C为顶点的三角形是直角三角形时,求出点P的坐标.
26.(本小题满分10分)在菱形ABCD中,∠ABC=60°,点P是对角线BD上一动点,将线段CP绕点C顺时针旋转120°到CQ,连接DQ.连接QP并延长,分别交AB,CD于点M,N.
(1)如图①,求证:△BCP≌△DCQ;
(2)如图②,已知PM=QN;若MN的最小值为2,求菱形ABCD的面积.
eq
\o(\s\up7(),\s\do5(图①))
eq
\o(\s\up7(),\s\do5(图②))
答案
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1.-3的绝对值是
(
B
)
A.-3
B.3
C.
D.-
2.疫情期间,高速免费79天,仅3月5日一天,高速免费惠及2650万辆车,累计减免通行费用达15亿元,将数字“15亿”用科学记数法表示为
(
C
)
A.2.65×107
B.265×104
C.1.5×109
D.
1.5×1010
3.在“美丽乡村”评选活动中,某乡镇7个村的得分为:86,98,90,88,96,92,96,这组数据的中位数和众数分别是(
A
)
A.92,96
B.90,96
C.92,98
D.92,92
4.式子在实数范围内有意义,则x的取值范围是(
D
)
A.x=0
B.x≥0
C.x>-4
D.x≥-4
5.下列计算正确的是
(
A
)
A.6a3-a3=5a3
B.a3·a3=a9
C.(3a)2=6a2
D.a6÷a2=a3
6.如果a>b,那么下列结论一定正确的是
(
B
)
A.a-3<b-3
B.3-a<3-b
C.ac>bc
D.a2>b2
7.方程3x2-2x-1=0的根的情况是
(
A
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根
8.下列命题中,是假命题的是
(
D
)
A.两点确定一条直线
B.平行线之间的距离处处相等
C.角平分线上的点到这个角两边的距离相等
D.同位角相等
9.如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD=2,DB=3,AC=10,则AE等于
(
B
)
A.3
B.4
C.5
D.6
eq
\o(\s\up7(),\s\do5(第9题图))
eq
\o(\s\up7(),\s\do5(第10题图))
10.如图,A,B,C是⊙O上的三个点,∠AOB=58°,则∠BCA的度数是
(
D
)
A.58°
B.42°
C.32°
D.29°
11.如图,矩形ABCD的对角线AC,BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F.已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是
(
C
)
A.先增大,后减小
B.先减小,后增大
C.始终等于2.4
D.始终等于3
eq
\o(\s\up7(),\s\do5(第11题图))
eq
\o(\s\up7(),\s\do5(第12题图))
12.★如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是
(
C
)
A.①③ B.②④ C.①③④ D.②③④
二、填空题(本大题共6小题,每小题3分,共18分)
13.计算
=3.
14.分解因式:a3+2a2+a=a(a+1)2.
15.疫情期间,某校有6名教师志愿者进行值班,其中4名女教师志愿者,2名男教师志愿者,若随机抽取2人为组长,恰好抽到2名男教师志愿者的概率为.
17.如图,直线m∥n,∠1=70°,∠2=28°32′,
则∠A等于41°28′
.
eq
\o(\s\up7(),\s\do5(第16题图))
eq
\o(\s\up7(),\s\do5(第17题图))
17.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA=6,则阴影部分的面积为3+3π
.
18.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,对称轴为直线x=1,则下列结论:①>0;
②a+b+c=0;
③关于x的方程ax2+bx+c+2=0无实根,④ac-b+1=0;⑤OA·OB=-.其中正确结论有④⑤.
三、解答题(本大题共8小题,共66分)
19.(本题满分10分,每小题5分)
(1)计算:(-1)2
021-+2sin
30°+|-|
解:原式=-1-2+1+2
=2-2.
(2)解方程:+1=.
解:方程两边同乘(x-2)得
x-3+x-2=-3
解得x=1,
检验:当x=1时,x-2≠0,故x=1是此分式方程的解.
20.(本小题满分5分)如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(4,3).
(1)在图中作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
A1________,B1________,C1________;
(2)在x轴上作出点P,使PA+PC最小.(不写作法,保留作图痕迹)
解:(1)如图所示,△A1B1C1即为所求,
A1(-1,2),B1
(-3,1),C1
(-4,3);
故答案为(-1,2),(-3,1),(-4,3);
(2)如图所示,点P即为所求.
21.(本小题满分6分)如图,已知一次函数y=kx+b的图象与反比例函数y=-的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
(1)一次函数的解析式;
(2)△AOB的面积.
解:(1)由题意A(-2,4),B(4,-2),
∵一次函数过A,B两点,
∴解得
∴一次函数的解析式为y=-x+2;
(2)设直线AB与y轴交于C,则C(0,2),
∵S△AOC=×OC×|xA|,S△BOC=×OC×|xB|
∴S△AOB=S△AOC+S△BOC=·OC·|xA|+·OC·|xB|
=×2×2+×2×4=6.
22.(本小题满分8分)疫情过去复学后,某校为了了解学生对疫情防控知识的掌握情况,随机抽测了本校部分学生进行了测试,共10个题,并将测试得到的情况绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=____%,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是____个、____个.
(3)该校共有学生2
400人,如果答对题达6个以上(含6个)为合格,请你估计该校学生对疫情防控知识掌握合格的有多少名?
解:(1)扇形统计图中a=1-30%-15%-10%-20%=25%,
设答对6个题的学生有x人,由题意得=,解得x=50.
补全条形统计图如图所示:
(2)
由条形图可知,答对5个题的学生有60人,人数最多,
所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,
故中位数为(5+5)÷2=5.
(3)×2
400=1
080(名).
答:估计该校对疫情防控知识掌握合格的同学有1
080名.
23.(本小题满分8分)(2020·百色模拟)高铁苏州北站已于几年前投入使用,计划在广场内种植A,B两种花木共10
500棵,若B花木数量是A花木数量的一半多1
500棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排27人同时种植这两种花木,每人每天能种植A花木50棵或B花木30棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
解:(1)设A花木的数量是x棵,B花木的数量是y棵,根据题意可得:解得
答:A花木的数量是6
000棵,B花木的数量是4
500棵;
(2)设安排a人种植A花木,则安排(27-a)人种植B花木,
=,
解得a=12,经检验,a=12是原方程的解,
∴27-a=15,
答:安排12人种植A花木,15人种植B花木,才能确保同时完成各自的任务.
24.(本小题满分8分)(2020·贵港港南区一模)如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC,AB的长.
(1)证明:连接OC.
∵点C在⊙O上,OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,∴∠DAC=∠OCA.
∵CD⊥PA,
∴∠CDA=90°,∴∠CAD+∠DCA=90°,
∴∠DCO=∠DCA+∠ACO=∠DCA+∠DAC=90°,
∵点C是⊙O上一点,
∴CD是⊙O切线.
(2)解:作OF⊥AB于F,
∴∠OCD=∠CDF=∠OFD=90°,
∴四边形CDFO是矩形,∴OC=FD,OF=CD,
∵CD=2AD,设AD=x,则OF=CD=2x,
∵DF=OC=10,
∴AF=10-x,
在Rt△AOF中,AF2+OF2=OA2,
∴(10-x)2+(2x)2=102,
解得x=4或0(舍去),
∴AD=4,AF=6,OF=CD+8.
∴AC==4,
∵OF⊥AB,
∴AB=2AF=2·=12.
25.(本小题满分11分)(2020·贵港港南区一模)如图,已知抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0).
(1)求该抛物线的表达式;
(2)点E是线段BC上方的抛物线上一个动点,求△BEC的面积的最大值;
(3)点P是抛物线的对称轴上一个动点,当以A,P,C为顶点的三角形是直角三角形时,求出点P的坐标.
解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0),
∴解得
∴y=-x2+2x+3=-(x-1)2+4;
(2)如解图,作EF∥y轴交BC于点F,记△BEC的面积为S,
∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3.
设E(m,-m2+2m+3)(0
解图
∴S=EF·OB=(-m2+3m)×3=-(m-)2+.
∵-<0,0
此时,点E的坐标是(,).
(3)
∵抛物线对称轴为直线x=1,∴可设P(1,n),
∵A(-1,0),C(0,3),
∴AC2=10,AP2=4+n2,CP2=1+(n-3)2=n2-6n+10.
①当AC⊥AP时,AC2+AP2=CP2,
即10+4+n2=n2-6n+10.
解得n=-;
②当AC⊥CP时,AC2+CP2=AP2,
即10+n2-6n+10=4+n2,
解得n=;
③当AP⊥CP时,AP2+CP2=AC2,
即4+n2+n2-6n+10=10.
解得n=1或2.
综上所述,符合条件的点P的坐标是(1,-)或(1,)或(1,1)或(1,2).
26.(本小题满分10分)在菱形ABCD中,∠ABC=60°,点P是对角线BD上一动点,将线段CP绕点C顺时针旋转120°到CQ,连接DQ.连接QP并延长,分别交AB,CD于点M,N.
(1)如图①,求证:△BCP≌△DCQ;
(2)如图②,已知PM=QN;若MN的最小值为2,求菱形ABCD的面积.
eq
\o(\s\up7(),\s\do5(图①))
eq
\o(\s\up7(),\s\do5(图②))
(1)证明:∵四边形ABCD是菱形,
∴BC=DC,AB∥CD,
∴∠PBM=∠PBC=∠ABC=30°,∠ABC+∠BCD=180°,
∴∠BCD=180°-∠ABC=120°
由旋转的性质得PC=QC,∠PCQ=120°,
∴∠BCD=∠PCQ,即∠BCP+∠PCD=∠DCQ+∠PCD,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
∴△BCP≌△DCQ(SAS);
(2)解:过点C作CG⊥PQ于点G,连接AC,
∵PC=QC,∠PCQ=120°,
∴∠PCG=60°,PG=QG,∴PG=PC,∴PQ=PC.
∵PM=QN,
∴MN=PQ=PC,
∴当PC⊥BD时,PC最小,此时MN最小,
∴PC=2,在Rt△BPC中,BC=2PC=4,
∵菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴S△ABC=×4×2=4,
∴菱形ABCD的面积=2S△ABC=2×4=8.
同课章节目录
