2020-2021学年七年级数学鲁教版下册《第8章平行线的证明》综合培优训练(word附答案)(五四制)
文档属性
| 名称 | 2020-2021学年七年级数学鲁教版下册《第8章平行线的证明》综合培优训练(word附答案)(五四制) |  | |
| 格式 | zip | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 14:05:43 | ||
图片预览



文档简介
2020-2021年度鲁教版七年级数学下册《第8章平行线的证明》综合培优训练(附答案)
1.如图,将一张三角形纸片ABC的三角折叠,使点A落在△ABC的A′处折痕为DE,若∠A=α,∠CEA′=β,∠BDA′=γ,那么下列式子中正确的是( )
A.γ=180°﹣α﹣β
B.γ=α+2β
C.γ=2α+β
D.γ=α+β
2.如图,直尺经过一块三角板DCB的直角顶点B,若将边AB绕点B顺时针旋转,∠ABC=20°,∠C=30°,则∠DEF度数为( )
A.25°
B.40°
C.50°
D.80°
3.如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为( )
A.120°
B.130°
C.140°
D.150°
4.如图,△ABC中,AE是BC边上的高,AD是∠BAC的平分线,∠B=42°,∠C=68°,∠DAE的度数( )
A.13°
B.15°
C.20°
D.22
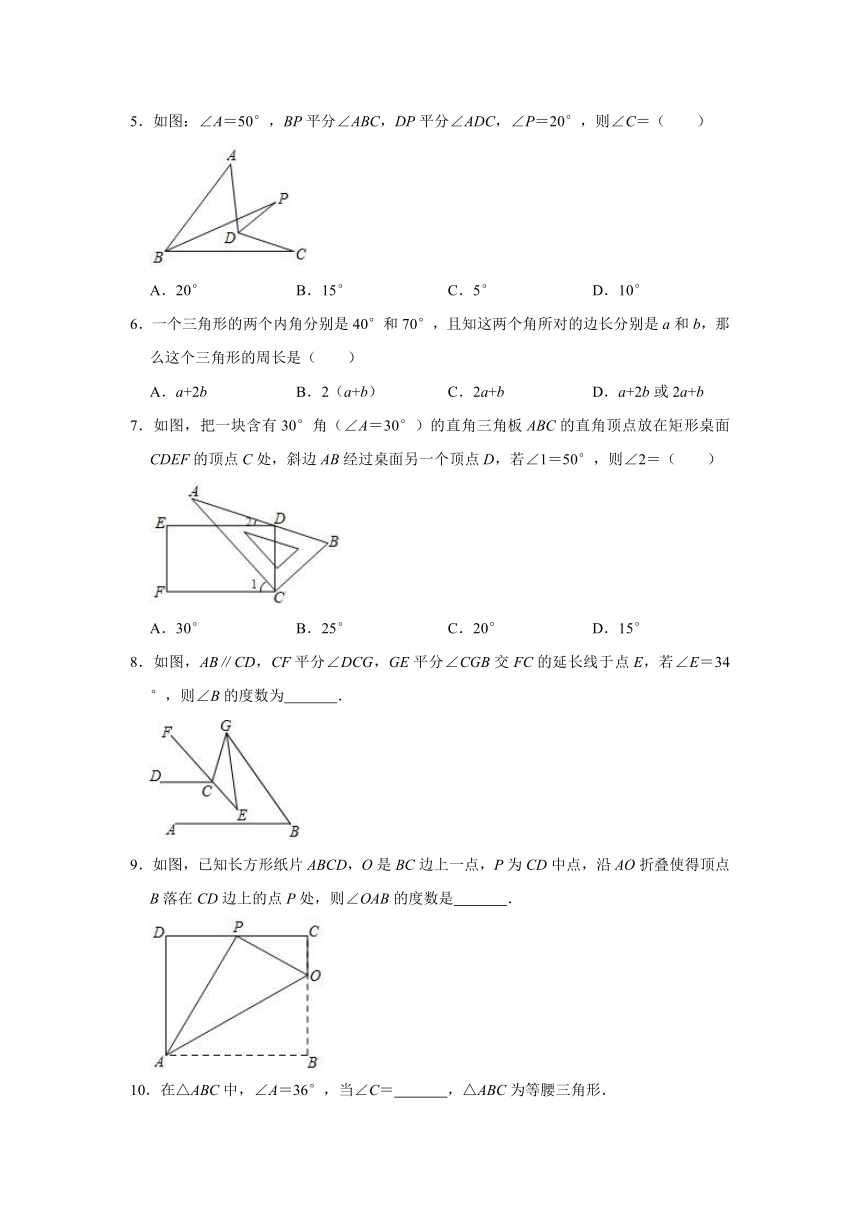
5.如图:∠A=50°,BP平分∠ABC,DP平分∠ADC,∠P=20°,则∠C=( )
A.20°
B.15°
C.5°
D.10°
6.一个三角形的两个内角分别是40°和70°,且知这两个角所对的边长分别是a和b,那么这个三角形的周长是( )
A.a+2b
B.2(a+b)
C.2a+b
D.a+2b或2a+b
7.如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在矩形桌面CDEF的顶点C处,斜边AB经过桌面另一个顶点D,若∠1=50°,则∠2=( )
A.30°
B.25°
C.20°
D.15°
8.如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为
.
9.如图,已知长方形纸片ABCD,O是BC边上一点,P为CD中点,沿AO折叠使得顶点B落在CD边上的点P处,则∠OAB的度数是
.
10.在△ABC中,∠A=36°,当∠C=
,△ABC为等腰三角形.
11.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为
.
12.△ABC中,若∠A=27.5°,∠B=30°25′,则∠C=
.
13.如图,已知AB∥DE,∠B=150°,∠D=145°,则∠C=
度.
14.如图,BP是△ABC的内角∠ABC的角平分线,交外角∠ACD的角平分线CP于点P,已知∠A=70°,则∠P的度数为
.
15.如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=80°,则∠CAP=
.
16.如图,∠ACD的平分线与∠ABD的平分线交于点E.∠A,∠CEB和∠D之间的数量关系是
.
17.如图,已知AB∥CD,则∠A、∠C、∠P的关系为
.
18.如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,则∠BMN的度数是
.
19.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为
.
20.已知∠1的两边分别平行于∠2的两边,若∠1=40°,则∠2的度数为
.
21.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
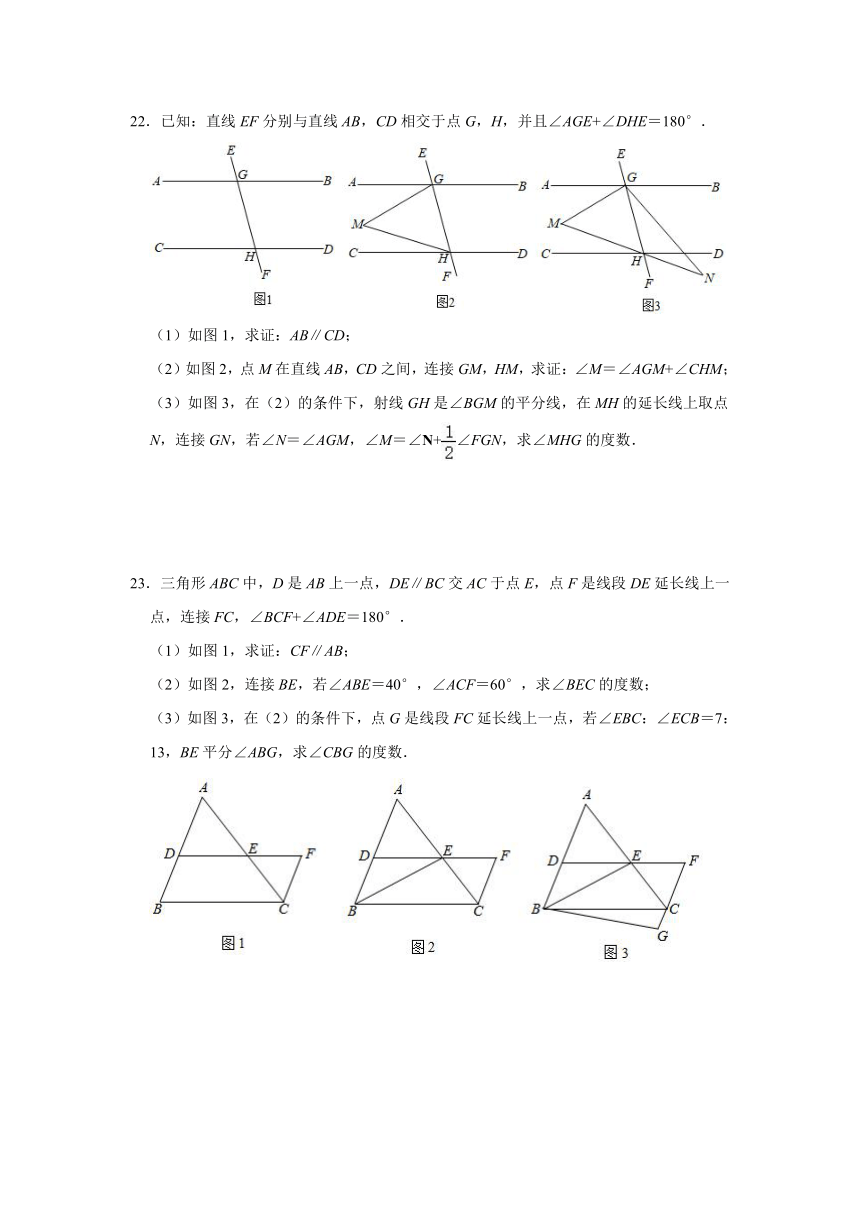
22.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
23.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
24.如图,∠1=52°,∠2=128°,∠C=∠D.探究∠A与∠F的数量关系,并说明理由.
25.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;
(3)联想拓展:在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系;
(4)解决问题:我们发现借助构造平行线的方法可以帮我们解决许多问题,随着以后的学习你还会发现平行线的许多用途.试构造平行线解决以下问题.
已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°
26.如图,CD⊥AB于D,EF⊥AB于F.
(1)求证:EF∥CD;
(2)若DE∥BC,EF平分∠AED,求证:CD平分∠ACB.
27.如图,点C在∠AOB的一边OA上,过点C的直线DE平行直线OB,CF平分∠ACD,CG⊥CF于点C.
(Ⅰ)若∠O=50°,求∠ACE的度数;
(Ⅱ)求证:CG平分∠OCD;
(Ⅲ)当∠O为多少度时,CD平分∠OCF,并说明理由.
参考答案
1.解:如图,设AC交DA′于F.
由折叠得:∠A=∠A',
∵∠BDA'=∠A+∠AFD,∠AFD=∠A'+∠CEA',
∵∠A=α,∠CEA′=β,∠BDA'=γ,
∴∠BDA'=γ=α+α+β=2α+β,
故选:C.
2.解:∵∠DAB=∠C+∠ABC,∠C=30°,∠ABC=20°,
∴∠DAB=20°+30°=50°,
∵EF∥AB,
∴∠DEF=∠DAB=50°,
故选:C.
3.解:∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),
∵∠A=100°,
∴∠OBC+∠OCB=(180°﹣100°)=40°,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣40°
=140°.
故选:C.
4.解:∵∠B=42°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=70°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=35°,
∵AE是BC边上的高,
∴∠AEC=90°,
∵∠C=68°,
∴∠EAC=180°﹣∠AEC﹣∠C=22°,
∴∠DAE=∠DAC﹣∠EAC=35°﹣22°=13°.
故选:A.
5.解:如图,延长PD交BC于M.设∠ADP=∠CDP=x,∠ABP=∠PBC=y.
∵∠ADC=∠A+∠ABC+∠C,
∴2x=2y+50°+∠C①
∵∠PDC=∠DMC+∠C,∠DMC=∠PBC+∠P,
∴x=∠C+∠P+y,
∴x=∠C+20°+y②,
①代入②可得∠C=10°,
故选:D.
6.解:如图,△ABC中,∠A=40°,∠B=70°,BC=a,AC=b.
∵∠C=180°﹣40°﹣70°=70°=∠B,
∴AB=AC=b,
∴△ABC的周长为a+2b.
故选:A.
7.解:
∵ED∥CF,
∴∠3=∠1=50°,
∵∠3=∠2+∠A,
∴∠2=∠3﹣∠A=50°﹣30°=20°.
故选:C.
8.解:如图,延长DC交BG于M.由题意可以假设∠DCF=∠GCF=x,∠CGE=∠MGE=y.
则有,
①﹣②×2可得:∠GMC=2∠E,
∵∠E=34°,
∴∠GMC=68°,
∵AB∥CD,
∴∠GMC=∠B=68°,
故答案为68°.
9.解:由折叠得,∠BAO=∠OAP,AB=AP,
∵长方形纸片ABCD,
∴AB=CD,∠D=∠DAB=∠B=90°,
∵P为CD中点,
∴PC=PD=CD=AP,
在Rt△ADP中,∠DAP=30°,
∴∠OAB=∠OAP=(90°﹣30°)=30°,
故答案为:30°.
10.解:①当AB=AC时,
∵∠A=36°,
∴∠C=∠B=72°.
②当CA=CB时,
∵∠A=∠B=36°,
∴∠C=108°.
③当BA=BC时,
∴∠C=∠A=36°,
综上所述,∠C的值为72°或108°或36°,
故答案为:72°,36°,108°.
11.解:如图,①当∠ABP1=∠DCA时,即∠1=∠2,
∵∠D=120°,
∴∠1+∠3=180°﹣120°=60°,
∵∠BAD=3∠CAD,∠ABE=2∠CBE,AD∥BC,
∴3∠3+3∠EBC=180°,
∴∠3+∠EBC=60°,
∴∠EBC=∠1=∠2=∠P1BE,
∴∠CBP1:∠ABP1的值为2,
②当∠ABP2=∠DCA时,∴∠CBP2:∠ABP2的值为4,
故答案为:2或4.
12.解:∵∠A=27.5°,∠B=30°25′,
∴∠C=180°﹣∠A﹣∠B=180°﹣27.5°﹣30°25′=122°5′,
故答案为:122°5′.
13.解:过点C作CF平行于AB,如图:
∵AB∥DE,
∴AB∥CF∥ED.
AB∥CF?∠1=180°﹣∠B=30°,
CF∥ED?∠2=180°﹣∠D=35°,
∴∠BCD=∠1+∠2=65°.
故填65°.
14.解:∵BP平分∠ABC,
∴∠CBP=∠ABC,
∵CP平分△ABC的外角,
∴∠PCD=∠ACE=(∠A+∠ABC)=∠A+∠ABC,
在△BCP中,由三角形的外角性质,∠PCE=∠CBP+∠P=∠ABC+∠P,
∴∠A+∠ABC=∠ABC+∠P,
∴∠P=∠BAC=×70°=35°.
故答案为:35°.
15.解:延长BA,作PN⊥BD于点N,PF⊥BA于点F,PM⊥AC于点M,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=80°,
∴∠ABP=∠PBC=(x﹣80)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣80°)﹣(x°﹣80°)=160°,
∴∠CAF=20°,
在Rt△PFA和Rt△PMA中,
,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=10°.
故答案为10°.
16.解:如图,延长AC交BD于M.设∠ABE=∠EBD=x,∠ACE=∠ECD=y.
∵∠AMD=∠A+∠ABD=∠A+2x,∠ECD=∠CEB+∠EBD+∠D=∠CEB+x+∠D,
∴∠ACD=2∠ECD=2∠CEB+2x+2∠D,
∵∠ACD=∠AMD+∠D,
∴∠AMD=2∠CEB+2x+2∠D﹣∠D=2∠CEB+2x+∠D
∴∠A+2x=2∠CEB+2x+∠D,
∴∠A=2∠CEB+∠D,
故答案为:∠A=2∠CEB+∠D.
17.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
18.解:如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,
∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N,
∴BN平分∠MBC,CN平分∠MCB,
∴NE=NG,NF=NG,
∴NE=NF,
∴MN平分∠BMC,
∴∠BMN=∠BMC,
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,
根据三等分,∠MBC+∠MCB=(∠ABC+∠ACB)=×120°=80°,
在△BMC中,∠BMC=180°﹣(∠MBC+∠MCB)=180°﹣80°=100°,
∴∠BMN=×100°=50°,
故答案为:50°.
19.解:∵∠DCE=∠DEC,∠DFG=∠DGF,
∴设∠DCE=∠DEC=x°,∠DFG=∠DGF=y°,
则∠FEG=∠DEC=x°,
∵在△GFE中,∠EFG=35°,
∴∠FEG+∠DGF=x°+y°=180°﹣35°=145°,
即x+y=145,
在△FDC中,∠CDF=180°﹣∠DCE﹣∠DFC=180°﹣x°﹣(y°﹣35°)
=215°﹣(x°+y°)
=70°,
故答案为:70°.
20.解:①若∠1与∠2位置如图1所示:
∵AB∥DE,
∴∠1=∠3,
又∵DC∥EF,
∴∠2=∠3,
∴∠1=∠2,
又∵∠1=40°,
∴∠2=40°;
②若∠1与∠2位置如图2所示:
∵AB∥DE,
∴∠1=∠3,
又∵DC∥EF,
∴∠2+∠3=180°,
∴∠2+∠1=180°,
又∵∠1=40°
∴∠2=180°﹣∠1=180°﹣40°=140°,
综合所述:∠2的度数为40°或140°,
故答案为:40°或140°.
21.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
22.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
23.(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠BCF+∠ADE=180°.
∴∠BCF+∠B=180°.
∴CF∥AB;
(2)解:如图2,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(3)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.
24.解:∠A=∠F,
理由是:∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
25.解:(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=50°+60°=110°;
(2)∠APC=α+β,
理由是:如图2,过P作PE∥AB,交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠APE=∠PAB=α,∠CPE=∠PCD=β,
∴∠APC=∠APE+∠CPE=α+β,
(3)如图3,所示,当P在BD延长线上时,
过P作PE∥AB,交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠PAB=α,
∵∠1=∠APC+∠PCD
∴∠APC=∠1﹣∠PCD,
∴∠APC=α﹣β,(9分)
如图4所示,当P在DB延长线上时,
同理可得:∠APC=β﹣α,
(4)证明:如图5,过点A作MN∥BC,
∴∠B=∠1,∠C=∠2,
∵∠BAC+∠1+∠2=180°,
∴∠BAC+∠B+∠C=180°.
26.证明:(1)∵CD⊥AB于D,EF⊥AB于F.
∴∠BDC=∠EFB=90°,
∴EF∥CD;
(2)∵EF平分∠AED,
∴∠AEF=∠DEF,
∵DE∥BC,EF∥CD,
∴∠AEF=∠ACD,∠DEF=∠CDE=∠BCD,
∴∠ACD=∠BCD,
∴CD平分∠ACB.
27.(Ⅰ)解:∵DE∥OB,
∴∠ACE=∠O,
∵∠O=50°,
∴∠ACE=50°;
(Ⅱ)证明:∵CG⊥CF,
∴∠FCG=90°,
∴∠DCF+∠DCG=90°,
又∵∠GCO+∠GCD+∠FCA+∠FCD=180°(平角定义),
∴∠GCO+∠FCA=90°,
∵CF平分∠ACD,
∴∠FCA=∠DCF,
∴∠GCO=∠DCG(等角的余角相等),
即CG平分∠OCD;
(Ⅲ)结论:当∠O=60°时,CD平分∠OCF,
当∠O=60°时,
∵DE∥OB,
∴∠DCO=∠O=60°,
∴∠ACD=120°,
又∵CF平分∠ACD,
∴∠DCF=60°,
∴∠DCO=∠DCF,
即CD平分∠OCF;
1.如图,将一张三角形纸片ABC的三角折叠,使点A落在△ABC的A′处折痕为DE,若∠A=α,∠CEA′=β,∠BDA′=γ,那么下列式子中正确的是( )
A.γ=180°﹣α﹣β
B.γ=α+2β
C.γ=2α+β
D.γ=α+β
2.如图,直尺经过一块三角板DCB的直角顶点B,若将边AB绕点B顺时针旋转,∠ABC=20°,∠C=30°,则∠DEF度数为( )
A.25°
B.40°
C.50°
D.80°
3.如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为( )
A.120°
B.130°
C.140°
D.150°
4.如图,△ABC中,AE是BC边上的高,AD是∠BAC的平分线,∠B=42°,∠C=68°,∠DAE的度数( )
A.13°
B.15°
C.20°
D.22
5.如图:∠A=50°,BP平分∠ABC,DP平分∠ADC,∠P=20°,则∠C=( )
A.20°
B.15°
C.5°
D.10°
6.一个三角形的两个内角分别是40°和70°,且知这两个角所对的边长分别是a和b,那么这个三角形的周长是( )
A.a+2b
B.2(a+b)
C.2a+b
D.a+2b或2a+b
7.如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在矩形桌面CDEF的顶点C处,斜边AB经过桌面另一个顶点D,若∠1=50°,则∠2=( )
A.30°
B.25°
C.20°
D.15°
8.如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为
.
9.如图,已知长方形纸片ABCD,O是BC边上一点,P为CD中点,沿AO折叠使得顶点B落在CD边上的点P处,则∠OAB的度数是
.
10.在△ABC中,∠A=36°,当∠C=
,△ABC为等腰三角形.
11.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为
.
12.△ABC中,若∠A=27.5°,∠B=30°25′,则∠C=
.
13.如图,已知AB∥DE,∠B=150°,∠D=145°,则∠C=
度.
14.如图,BP是△ABC的内角∠ABC的角平分线,交外角∠ACD的角平分线CP于点P,已知∠A=70°,则∠P的度数为
.
15.如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=80°,则∠CAP=
.
16.如图,∠ACD的平分线与∠ABD的平分线交于点E.∠A,∠CEB和∠D之间的数量关系是
.
17.如图,已知AB∥CD,则∠A、∠C、∠P的关系为
.
18.如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,则∠BMN的度数是
.
19.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为
.
20.已知∠1的两边分别平行于∠2的两边,若∠1=40°,则∠2的度数为
.
21.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
22.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
23.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
24.如图,∠1=52°,∠2=128°,∠C=∠D.探究∠A与∠F的数量关系,并说明理由.
25.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;
(3)联想拓展:在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系;
(4)解决问题:我们发现借助构造平行线的方法可以帮我们解决许多问题,随着以后的学习你还会发现平行线的许多用途.试构造平行线解决以下问题.
已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°
26.如图,CD⊥AB于D,EF⊥AB于F.
(1)求证:EF∥CD;
(2)若DE∥BC,EF平分∠AED,求证:CD平分∠ACB.
27.如图,点C在∠AOB的一边OA上,过点C的直线DE平行直线OB,CF平分∠ACD,CG⊥CF于点C.
(Ⅰ)若∠O=50°,求∠ACE的度数;
(Ⅱ)求证:CG平分∠OCD;
(Ⅲ)当∠O为多少度时,CD平分∠OCF,并说明理由.
参考答案
1.解:如图,设AC交DA′于F.
由折叠得:∠A=∠A',
∵∠BDA'=∠A+∠AFD,∠AFD=∠A'+∠CEA',
∵∠A=α,∠CEA′=β,∠BDA'=γ,
∴∠BDA'=γ=α+α+β=2α+β,
故选:C.
2.解:∵∠DAB=∠C+∠ABC,∠C=30°,∠ABC=20°,
∴∠DAB=20°+30°=50°,
∵EF∥AB,
∴∠DEF=∠DAB=50°,
故选:C.
3.解:∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),
∵∠A=100°,
∴∠OBC+∠OCB=(180°﹣100°)=40°,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣40°
=140°.
故选:C.
4.解:∵∠B=42°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=70°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=35°,
∵AE是BC边上的高,
∴∠AEC=90°,
∵∠C=68°,
∴∠EAC=180°﹣∠AEC﹣∠C=22°,
∴∠DAE=∠DAC﹣∠EAC=35°﹣22°=13°.
故选:A.
5.解:如图,延长PD交BC于M.设∠ADP=∠CDP=x,∠ABP=∠PBC=y.
∵∠ADC=∠A+∠ABC+∠C,
∴2x=2y+50°+∠C①
∵∠PDC=∠DMC+∠C,∠DMC=∠PBC+∠P,
∴x=∠C+∠P+y,
∴x=∠C+20°+y②,
①代入②可得∠C=10°,
故选:D.
6.解:如图,△ABC中,∠A=40°,∠B=70°,BC=a,AC=b.
∵∠C=180°﹣40°﹣70°=70°=∠B,
∴AB=AC=b,
∴△ABC的周长为a+2b.
故选:A.
7.解:
∵ED∥CF,
∴∠3=∠1=50°,
∵∠3=∠2+∠A,
∴∠2=∠3﹣∠A=50°﹣30°=20°.
故选:C.
8.解:如图,延长DC交BG于M.由题意可以假设∠DCF=∠GCF=x,∠CGE=∠MGE=y.
则有,
①﹣②×2可得:∠GMC=2∠E,
∵∠E=34°,
∴∠GMC=68°,
∵AB∥CD,
∴∠GMC=∠B=68°,
故答案为68°.
9.解:由折叠得,∠BAO=∠OAP,AB=AP,
∵长方形纸片ABCD,
∴AB=CD,∠D=∠DAB=∠B=90°,
∵P为CD中点,
∴PC=PD=CD=AP,
在Rt△ADP中,∠DAP=30°,
∴∠OAB=∠OAP=(90°﹣30°)=30°,
故答案为:30°.
10.解:①当AB=AC时,
∵∠A=36°,
∴∠C=∠B=72°.
②当CA=CB时,
∵∠A=∠B=36°,
∴∠C=108°.
③当BA=BC时,
∴∠C=∠A=36°,
综上所述,∠C的值为72°或108°或36°,
故答案为:72°,36°,108°.
11.解:如图,①当∠ABP1=∠DCA时,即∠1=∠2,
∵∠D=120°,
∴∠1+∠3=180°﹣120°=60°,
∵∠BAD=3∠CAD,∠ABE=2∠CBE,AD∥BC,
∴3∠3+3∠EBC=180°,
∴∠3+∠EBC=60°,
∴∠EBC=∠1=∠2=∠P1BE,
∴∠CBP1:∠ABP1的值为2,
②当∠ABP2=∠DCA时,∴∠CBP2:∠ABP2的值为4,
故答案为:2或4.
12.解:∵∠A=27.5°,∠B=30°25′,
∴∠C=180°﹣∠A﹣∠B=180°﹣27.5°﹣30°25′=122°5′,
故答案为:122°5′.
13.解:过点C作CF平行于AB,如图:
∵AB∥DE,
∴AB∥CF∥ED.
AB∥CF?∠1=180°﹣∠B=30°,
CF∥ED?∠2=180°﹣∠D=35°,
∴∠BCD=∠1+∠2=65°.
故填65°.
14.解:∵BP平分∠ABC,
∴∠CBP=∠ABC,
∵CP平分△ABC的外角,
∴∠PCD=∠ACE=(∠A+∠ABC)=∠A+∠ABC,
在△BCP中,由三角形的外角性质,∠PCE=∠CBP+∠P=∠ABC+∠P,
∴∠A+∠ABC=∠ABC+∠P,
∴∠P=∠BAC=×70°=35°.
故答案为:35°.
15.解:延长BA,作PN⊥BD于点N,PF⊥BA于点F,PM⊥AC于点M,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=80°,
∴∠ABP=∠PBC=(x﹣80)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣80°)﹣(x°﹣80°)=160°,
∴∠CAF=20°,
在Rt△PFA和Rt△PMA中,
,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=10°.
故答案为10°.
16.解:如图,延长AC交BD于M.设∠ABE=∠EBD=x,∠ACE=∠ECD=y.
∵∠AMD=∠A+∠ABD=∠A+2x,∠ECD=∠CEB+∠EBD+∠D=∠CEB+x+∠D,
∴∠ACD=2∠ECD=2∠CEB+2x+2∠D,
∵∠ACD=∠AMD+∠D,
∴∠AMD=2∠CEB+2x+2∠D﹣∠D=2∠CEB+2x+∠D
∴∠A+2x=2∠CEB+2x+∠D,
∴∠A=2∠CEB+∠D,
故答案为:∠A=2∠CEB+∠D.
17.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
18.解:如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,
∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N,
∴BN平分∠MBC,CN平分∠MCB,
∴NE=NG,NF=NG,
∴NE=NF,
∴MN平分∠BMC,
∴∠BMN=∠BMC,
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,
根据三等分,∠MBC+∠MCB=(∠ABC+∠ACB)=×120°=80°,
在△BMC中,∠BMC=180°﹣(∠MBC+∠MCB)=180°﹣80°=100°,
∴∠BMN=×100°=50°,
故答案为:50°.
19.解:∵∠DCE=∠DEC,∠DFG=∠DGF,
∴设∠DCE=∠DEC=x°,∠DFG=∠DGF=y°,
则∠FEG=∠DEC=x°,
∵在△GFE中,∠EFG=35°,
∴∠FEG+∠DGF=x°+y°=180°﹣35°=145°,
即x+y=145,
在△FDC中,∠CDF=180°﹣∠DCE﹣∠DFC=180°﹣x°﹣(y°﹣35°)
=215°﹣(x°+y°)
=70°,
故答案为:70°.
20.解:①若∠1与∠2位置如图1所示:
∵AB∥DE,
∴∠1=∠3,
又∵DC∥EF,
∴∠2=∠3,
∴∠1=∠2,
又∵∠1=40°,
∴∠2=40°;
②若∠1与∠2位置如图2所示:
∵AB∥DE,
∴∠1=∠3,
又∵DC∥EF,
∴∠2+∠3=180°,
∴∠2+∠1=180°,
又∵∠1=40°
∴∠2=180°﹣∠1=180°﹣40°=140°,
综合所述:∠2的度数为40°或140°,
故答案为:40°或140°.
21.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
22.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
23.(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠BCF+∠ADE=180°.
∴∠BCF+∠B=180°.
∴CF∥AB;
(2)解:如图2,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(3)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.
24.解:∠A=∠F,
理由是:∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
25.解:(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=50°+60°=110°;
(2)∠APC=α+β,
理由是:如图2,过P作PE∥AB,交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠APE=∠PAB=α,∠CPE=∠PCD=β,
∴∠APC=∠APE+∠CPE=α+β,
(3)如图3,所示,当P在BD延长线上时,
过P作PE∥AB,交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠PAB=α,
∵∠1=∠APC+∠PCD
∴∠APC=∠1﹣∠PCD,
∴∠APC=α﹣β,(9分)
如图4所示,当P在DB延长线上时,
同理可得:∠APC=β﹣α,
(4)证明:如图5,过点A作MN∥BC,
∴∠B=∠1,∠C=∠2,
∵∠BAC+∠1+∠2=180°,
∴∠BAC+∠B+∠C=180°.
26.证明:(1)∵CD⊥AB于D,EF⊥AB于F.
∴∠BDC=∠EFB=90°,
∴EF∥CD;
(2)∵EF平分∠AED,
∴∠AEF=∠DEF,
∵DE∥BC,EF∥CD,
∴∠AEF=∠ACD,∠DEF=∠CDE=∠BCD,
∴∠ACD=∠BCD,
∴CD平分∠ACB.
27.(Ⅰ)解:∵DE∥OB,
∴∠ACE=∠O,
∵∠O=50°,
∴∠ACE=50°;
(Ⅱ)证明:∵CG⊥CF,
∴∠FCG=90°,
∴∠DCF+∠DCG=90°,
又∵∠GCO+∠GCD+∠FCA+∠FCD=180°(平角定义),
∴∠GCO+∠FCA=90°,
∵CF平分∠ACD,
∴∠FCA=∠DCF,
∴∠GCO=∠DCG(等角的余角相等),
即CG平分∠OCD;
(Ⅲ)结论:当∠O=60°时,CD平分∠OCF,
当∠O=60°时,
∵DE∥OB,
∴∠DCO=∠O=60°,
∴∠ACD=120°,
又∵CF平分∠ACD,
∴∠DCF=60°,
∴∠DCO=∠DCF,
即CD平分∠OCF;
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
