2020-2021学年人教版八年级数学下册 第十九章 一次函数 19.1.2 函数的图像 课后练习(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册 第十九章 一次函数 19.1.2 函数的图像 课后练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 250.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 15:50:28 | ||
图片预览


文档简介
人教版八年级数学下册
第十九章
一次函数
19.1.2
函数的图像
课后练习
一、选择题
1.已知点
P(x,y)在函数的图象上,那么点
P
应在平面直角坐标系中的(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.下面哪个点不在函数的图像上(
)
A.(3,0)
B.(0.5,2)
C.(-5,13)
D.(1,1)
3.某地区植树造林2007年达到2万公顷,预计从2008年开始以后每年比前一年多植树1万公顷(2008年为第一年),则年植树面积y(万亩)与年数x(年)的关系是(
)
A.
B.
C.
D.
4.已知y关于x的函数图象如图所示,则图中当时,自变量x的取值范围是(
)
A.
B.或
C.
D.或
5.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )
A.4℃
B.8℃
C.12℃
D.16℃
6.小强每天从家到学校上学行走的路程为900m,某天他从家去上学时以每分30m的速度行走了450m,为了不迟到他加快了速度,以每分45m的速度行走完剩下的路程,那么小强离学校的路程s(m)与他行走的时间t(min)之间的函数关系用图象表示正确的是(
)
A.B.C.
D.
7.下列图象不能反映是的函数的是(
)
A.B.C.D.
8.下列图形中的曲线不表示y是x的函数的是(
)
A.
B.C.
D.
9.表示皮球从高处d落下时,弹跳高度b与下落高度d的关系如下表所示:则d与b之间的关系式为(
)
下落高度d
…
80
100
150
…
弹跳高度b
…
40
50
75
…
A.b=d-40
B.b=
C.b=d2
D.b=2d
10.周末,小明骑自行车从家里出发去游玩。从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,则下列说法中正确的是(
)
A.小明在迪诺水镇游玩1h后,经过h到达万达广场
B.小明的速度是20km/h,妈妈的速度是60km/h
C.万达广场离小明家26km
D.点C的坐标为(,25)
二、填空题
11.设地面气温为20℃,如果每升高1km,气温下降6℃.如果高度用h(km)表示,气温用t(℃)表示,那么t随h的变化而变化的关系式为_____.
12.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离(单位:米)与时间(单位:分钟)的对应关系如图所示,则文具店与小张家的距离为_________.
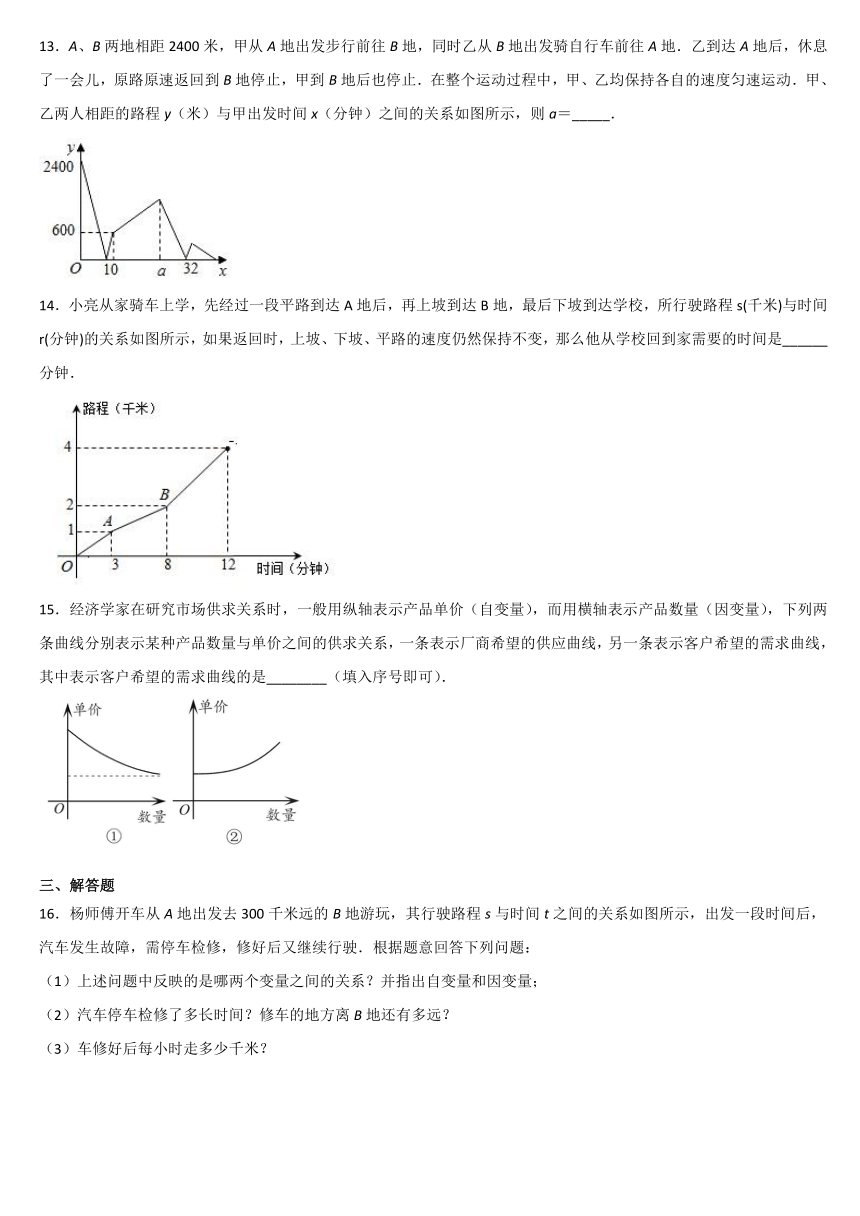
13.A、B两地相距2400米,甲从A地出发步行前往B地,同时乙从B地出发骑自行车前往A地.乙到达A地后,休息了一会儿,原路原速返回到B地停止,甲到B地后也停止.在整个运动过程中,甲、乙均保持各自的速度匀速运动.甲、乙两人相距的路程y(米)与甲出发时间x(分钟)之间的关系如图所示,则a=_____.
14.小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间r(分钟)的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是______分钟.
15.经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是________(填入序号即可).
三、解答题
16.杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:
(1)上述问题中反映的是哪两个变量之间的关系?并指出自变量和因变量;
(2)汽车停车检修了多长时间?修车的地方离B地还有多远?
(3)车修好后每小时走多少千米?
17.一个安有进水管和出水管的蓄水池,每单位时间内进水量分别是一定的.若从某时刻开始的4小时内只进水不出水,在随后的8小时内既进水又出水,得到时间x(小时)与蓄水池内水量之间的关系如图所示.
(1)求进水管进水和出水管出水的速度;
(2)如果12小时后只放水,不进水,求此时y随x变化而变化的关系式.
18.如图,lA与
lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距多少千米?
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时?
(3)B出发后经过多少小时与A相遇?
19.如图,这是一个水池存水量(万吨)与注水或排水时间(小时)之间的函数关系图象.
(1)水池原有水_________;
(2)向水池内注水________小时;每小时注水_______万吨;
(3)________小时把水排空;每小时排水________万吨.
20.如图是某地方春季一天的气温随时间的变化图象.请根据图象回答:
(1)何时气温最低?最低气温是多少?
(2)当天的最高气温是多少?这一天最大温差是多少?
21.2020年,周至县小李家的猕猴桃喜获丰收.在销售过程中,猕猴桃的销售额y(元)与销量x(千克)满足如下关系:
销售量x(千克)
1
2
3
4
5
6
7
8
销售额y(元)
6
12
18
24
30
36
42
48
(1)在这个变化过程中,自变量是_________,因变量是_________;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为_________;
(3)当猕猴桃销售量为100千克时,销售额是多少元?
22.画出y=2x﹣4的图象,确定x取何值时,
(1)y0;
(2)y﹣4.
23.心理学家发现,学生对概念的接受能力与提出概念所用的时间(单位:分)之间有如下关系:(其中)
提出概念所用时间
对概念的接受能力
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用时间为几分钟时,学生的接受能力最强?
(4)从表中可知,当时间在什么范围内,学生的接受能力逐步增强?当时间在什么范围内,学生的接受能力逐步降低?
【参考答案】
1.B
2.A
3.B
4.D
5.C
6.D
7.A
8.C
9.B
10.B
11.t=﹣6h+20
12.900m
13.24
14.15
15.①
16.(1)上述问题中反映的是行驶路程与行驶时间的关系;自变量是行驶时间,因变量是行驶路程.(2)汽车停车检修了1小时;修车的地方离B地还有150千米.(3)车修好后每小时走75千米.
17.(1)进水管速度5,出水速度;(2).
18.(1)10千米;(2)1小时;(3)B出发后3小时与A相遇.
19.(1)100万吨;(2)3,50;(3)5,50.
20.(1)4时气温最低,最低气温是-2℃;(2)最高气温是9℃,温差是11℃
21.(1)猕猴桃的销售量,猕猴桃的销售额;(2);(3)当猕猴桃销量为100千克时,销售额是600元.
22.图见解析;(1)
;(2)
23.(1)提出概念所用的时间和对概念的接受能力两个变量之间的关系,提出概念所用时间是自变量,对概念的接受能力是因变量;(2);(3)提出概念所用时间为分钟时,学生的接受能力最强;(3)当时,值逐渐增大,学生的接受能力逐步增强;当时,值逐渐减小,学生的接受能力逐步降低
第十九章
一次函数
19.1.2
函数的图像
课后练习
一、选择题
1.已知点
P(x,y)在函数的图象上,那么点
P
应在平面直角坐标系中的(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.下面哪个点不在函数的图像上(
)
A.(3,0)
B.(0.5,2)
C.(-5,13)
D.(1,1)
3.某地区植树造林2007年达到2万公顷,预计从2008年开始以后每年比前一年多植树1万公顷(2008年为第一年),则年植树面积y(万亩)与年数x(年)的关系是(
)
A.
B.
C.
D.
4.已知y关于x的函数图象如图所示,则图中当时,自变量x的取值范围是(
)
A.
B.或
C.
D.或
5.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是( )
A.4℃
B.8℃
C.12℃
D.16℃
6.小强每天从家到学校上学行走的路程为900m,某天他从家去上学时以每分30m的速度行走了450m,为了不迟到他加快了速度,以每分45m的速度行走完剩下的路程,那么小强离学校的路程s(m)与他行走的时间t(min)之间的函数关系用图象表示正确的是(
)
A.B.C.
D.
7.下列图象不能反映是的函数的是(
)
A.B.C.D.
8.下列图形中的曲线不表示y是x的函数的是(
)
A.
B.C.
D.
9.表示皮球从高处d落下时,弹跳高度b与下落高度d的关系如下表所示:则d与b之间的关系式为(
)
下落高度d
…
80
100
150
…
弹跳高度b
…
40
50
75
…
A.b=d-40
B.b=
C.b=d2
D.b=2d
10.周末,小明骑自行车从家里出发去游玩。从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,则下列说法中正确的是(
)
A.小明在迪诺水镇游玩1h后,经过h到达万达广场
B.小明的速度是20km/h,妈妈的速度是60km/h
C.万达广场离小明家26km
D.点C的坐标为(,25)
二、填空题
11.设地面气温为20℃,如果每升高1km,气温下降6℃.如果高度用h(km)表示,气温用t(℃)表示,那么t随h的变化而变化的关系式为_____.
12.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离(单位:米)与时间(单位:分钟)的对应关系如图所示,则文具店与小张家的距离为_________.
13.A、B两地相距2400米,甲从A地出发步行前往B地,同时乙从B地出发骑自行车前往A地.乙到达A地后,休息了一会儿,原路原速返回到B地停止,甲到B地后也停止.在整个运动过程中,甲、乙均保持各自的速度匀速运动.甲、乙两人相距的路程y(米)与甲出发时间x(分钟)之间的关系如图所示,则a=_____.
14.小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间r(分钟)的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是______分钟.
15.经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是________(填入序号即可).
三、解答题
16.杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:
(1)上述问题中反映的是哪两个变量之间的关系?并指出自变量和因变量;
(2)汽车停车检修了多长时间?修车的地方离B地还有多远?
(3)车修好后每小时走多少千米?
17.一个安有进水管和出水管的蓄水池,每单位时间内进水量分别是一定的.若从某时刻开始的4小时内只进水不出水,在随后的8小时内既进水又出水,得到时间x(小时)与蓄水池内水量之间的关系如图所示.
(1)求进水管进水和出水管出水的速度;
(2)如果12小时后只放水,不进水,求此时y随x变化而变化的关系式.
18.如图,lA与
lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距多少千米?
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时?
(3)B出发后经过多少小时与A相遇?
19.如图,这是一个水池存水量(万吨)与注水或排水时间(小时)之间的函数关系图象.
(1)水池原有水_________;
(2)向水池内注水________小时;每小时注水_______万吨;
(3)________小时把水排空;每小时排水________万吨.
20.如图是某地方春季一天的气温随时间的变化图象.请根据图象回答:
(1)何时气温最低?最低气温是多少?
(2)当天的最高气温是多少?这一天最大温差是多少?
21.2020年,周至县小李家的猕猴桃喜获丰收.在销售过程中,猕猴桃的销售额y(元)与销量x(千克)满足如下关系:
销售量x(千克)
1
2
3
4
5
6
7
8
销售额y(元)
6
12
18
24
30
36
42
48
(1)在这个变化过程中,自变量是_________,因变量是_________;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为_________;
(3)当猕猴桃销售量为100千克时,销售额是多少元?
22.画出y=2x﹣4的图象,确定x取何值时,
(1)y0;
(2)y﹣4.
23.心理学家发现,学生对概念的接受能力与提出概念所用的时间(单位:分)之间有如下关系:(其中)
提出概念所用时间
对概念的接受能力
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用时间为几分钟时,学生的接受能力最强?
(4)从表中可知,当时间在什么范围内,学生的接受能力逐步增强?当时间在什么范围内,学生的接受能力逐步降低?
【参考答案】
1.B
2.A
3.B
4.D
5.C
6.D
7.A
8.C
9.B
10.B
11.t=﹣6h+20
12.900m
13.24
14.15
15.①
16.(1)上述问题中反映的是行驶路程与行驶时间的关系;自变量是行驶时间,因变量是行驶路程.(2)汽车停车检修了1小时;修车的地方离B地还有150千米.(3)车修好后每小时走75千米.
17.(1)进水管速度5,出水速度;(2).
18.(1)10千米;(2)1小时;(3)B出发后3小时与A相遇.
19.(1)100万吨;(2)3,50;(3)5,50.
20.(1)4时气温最低,最低气温是-2℃;(2)最高气温是9℃,温差是11℃
21.(1)猕猴桃的销售量,猕猴桃的销售额;(2);(3)当猕猴桃销量为100千克时,销售额是600元.
22.图见解析;(1)
;(2)
23.(1)提出概念所用的时间和对概念的接受能力两个变量之间的关系,提出概念所用时间是自变量,对概念的接受能力是因变量;(2);(3)提出概念所用时间为分钟时,学生的接受能力最强;(3)当时,值逐渐增大,学生的接受能力逐步增强;当时,值逐渐减小,学生的接受能力逐步降低
