2020-2021学年人教版八年级下册数学第18章《平行四边形》单元测试(word含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》单元测试(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 00:00:00 | ||
图片预览


文档简介
第18章
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
1.已知?ABCD中,∠B=∠A+∠C,则∠C=()
A.18°
B.36°
C.60°
D.144°
2.在平行四边形、矩形、菱形、正方形中,是轴对称图形的有()
A.1个
B.2个
C.3个
D.4个
3.如图,在?ABCD中,下列说法一定正确的是()
A.AB=CD
B.AB=BC
C.AC=BD
D.AC⊥BD
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
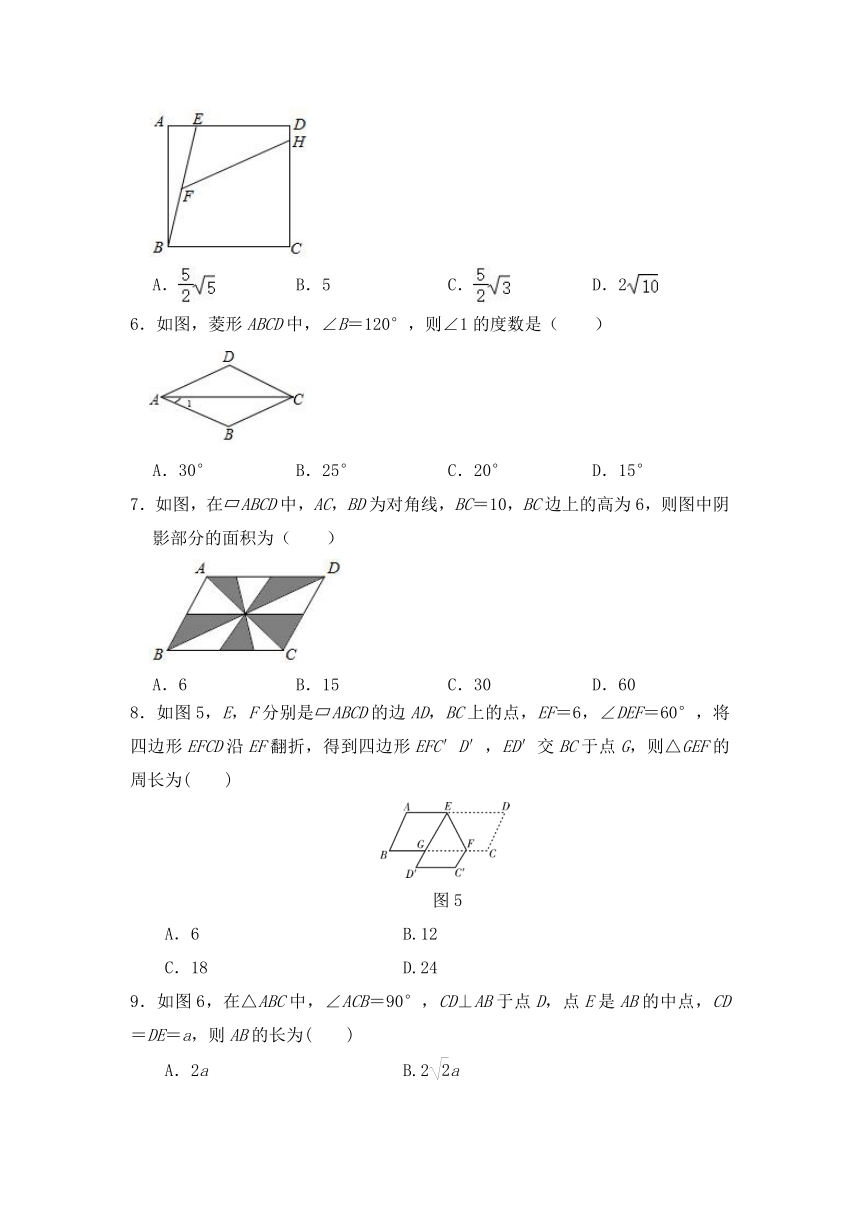
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图5,E,F分别是?ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到四边形EFC′D′,ED′交BC于点G,则△GEF的周长为( )
图5
A.6
B.12
C.18
D.24
9.如图6,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E是AB的中点,CD=DE=a,则AB的长为( )
A.2a
B.2a
C.3a
D.a
图6
10.如图7,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2,∠AEO=120°,则CF的长为( )
图7
A.1
B.2
C.
D.
二.填空题(每题4分,共20分)
11.
如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是
.
12.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.
13.已知三角形的三边长分别是4,5,6,则它的三条中位线围成的三角形的周长是____________.
14.如图,EF是纸片的中位线,将沿EF所在的直线折叠,点A落在BC边上的点D处,已知的面积为7,则图中阴影部分的面积为______
.
15.
在ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件。下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是__________。
三.解答题(每题10分,共50分)
16.两个完全相同的矩形纸片ABCD、A′BC′D如图放置,重叠部分是四边形BMDN.
(1)试证明四边形BNDM为菱形;
(2)MN与A′C是什么位置关系,试证明.
17.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形.
(2)求BC的长.
18.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
19.如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在AC上,.
求证:四边形BEDF是平行四边形;
若,,求AB的长.
20.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作,垂足为点H,延长BH交CD于点F,连接AF.
求证:.
若正方形边长是5,,求AF的长.
21.如图,在中,,,,点D从点C出发沿CA方向以秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒过点D作于点F,连接DE,EF.
试问四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由.
当t为何值时,?请说明理由.
参考答案
一.选择题
1.
C
2.
C.
3.
A.
4.
C.
5.
D.
6.
C.
7.
C.
8.
C.
9.
B.
10.A
二.填空题(共5小题)
11.
12.30
13.7.5
14、14
15、①②③
三.解答题(共5小题)
16.(1)证明:∵两个完全相同的矩形纸片ABCD、BA′DE,根据矩形的对边平行,
∴BC∥AD,BE∥DA′,
∴四边形BNDM是平行四边形,
∵∠ABM+∠MBN=90°,∠MBN+∠A′BN=90°,
∴∠ABM=∠A′BN.
在△ABM和△A′BN中,,
∴△ABM≌△A′BN,(ASA).
∴BM=BN,
∴四边形BNDM是菱形;
(2)解:MN垂直平分A′C,
在Rt△BA′N与Rt△CDN中,,
∴Rt△BA′N≌Rt△CDN,
∴A′N=CN,
∵∠BNM=∠DNM,∠A′NG=∠DNM,∠CNG=∠BNM,
∴∠A′NG=∠CNG,
∴MN垂直平分A′C.
17.解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD===2.
∵D是BC的中点,
∴BC=2CD=4.
18.证明:∵四边形ABCD为矩形,∴OB=OC.∵BE⊥AC于E,CF⊥BD于F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF(AAS).∴BE=CF.
19.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
20、证明:四边形ABCD是正方形,,,,
,,,,
在和中,,≌,;
解:,由得:≌,,,
四边形ABCD是正方形,,,
由勾股定理得:.
21、解:四边形AEFD能够成为菱形.?
理由如下:
在中,,,,?
又,.,,.
又,四边形AEFD为平行四边形.?
如图1,当时,四边形AEFD为菱形,
即,解得.
当秒时,四边形AEFD为菱形.
如图2,当时,四边形EBFD为矩形.?
在中,,则,,?
即,?解得.
当时,.
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
1.已知?ABCD中,∠B=∠A+∠C,则∠C=()
A.18°
B.36°
C.60°
D.144°
2.在平行四边形、矩形、菱形、正方形中,是轴对称图形的有()
A.1个
B.2个
C.3个
D.4个
3.如图,在?ABCD中,下列说法一定正确的是()
A.AB=CD
B.AB=BC
C.AC=BD
D.AC⊥BD
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图5,E,F分别是?ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到四边形EFC′D′,ED′交BC于点G,则△GEF的周长为( )
图5
A.6
B.12
C.18
D.24
9.如图6,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E是AB的中点,CD=DE=a,则AB的长为( )
A.2a
B.2a
C.3a
D.a
图6
10.如图7,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2,∠AEO=120°,则CF的长为( )
图7
A.1
B.2
C.
D.
二.填空题(每题4分,共20分)
11.
如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是
.
12.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.
13.已知三角形的三边长分别是4,5,6,则它的三条中位线围成的三角形的周长是____________.
14.如图,EF是纸片的中位线,将沿EF所在的直线折叠,点A落在BC边上的点D处,已知的面积为7,则图中阴影部分的面积为______
.
15.
在ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件。下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是__________。
三.解答题(每题10分,共50分)
16.两个完全相同的矩形纸片ABCD、A′BC′D如图放置,重叠部分是四边形BMDN.
(1)试证明四边形BNDM为菱形;
(2)MN与A′C是什么位置关系,试证明.
17.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形.
(2)求BC的长.
18.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
19.如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在AC上,.
求证:四边形BEDF是平行四边形;
若,,求AB的长.
20.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作,垂足为点H,延长BH交CD于点F,连接AF.
求证:.
若正方形边长是5,,求AF的长.
21.如图,在中,,,,点D从点C出发沿CA方向以秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒过点D作于点F,连接DE,EF.
试问四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由.
当t为何值时,?请说明理由.
参考答案
一.选择题
1.
C
2.
C.
3.
A.
4.
C.
5.
D.
6.
C.
7.
C.
8.
C.
9.
B.
10.A
二.填空题(共5小题)
11.
12.30
13.7.5
14、14
15、①②③
三.解答题(共5小题)
16.(1)证明:∵两个完全相同的矩形纸片ABCD、BA′DE,根据矩形的对边平行,
∴BC∥AD,BE∥DA′,
∴四边形BNDM是平行四边形,
∵∠ABM+∠MBN=90°,∠MBN+∠A′BN=90°,
∴∠ABM=∠A′BN.
在△ABM和△A′BN中,,
∴△ABM≌△A′BN,(ASA).
∴BM=BN,
∴四边形BNDM是菱形;
(2)解:MN垂直平分A′C,
在Rt△BA′N与Rt△CDN中,,
∴Rt△BA′N≌Rt△CDN,
∴A′N=CN,
∵∠BNM=∠DNM,∠A′NG=∠DNM,∠CNG=∠BNM,
∴∠A′NG=∠CNG,
∴MN垂直平分A′C.
17.解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD===2.
∵D是BC的中点,
∴BC=2CD=4.
18.证明:∵四边形ABCD为矩形,∴OB=OC.∵BE⊥AC于E,CF⊥BD于F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF(AAS).∴BE=CF.
19.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
20、证明:四边形ABCD是正方形,,,,
,,,,
在和中,,≌,;
解:,由得:≌,,,
四边形ABCD是正方形,,,
由勾股定理得:.
21、解:四边形AEFD能够成为菱形.?
理由如下:
在中,,,,?
又,.,,.
又,四边形AEFD为平行四边形.?
如图1,当时,四边形AEFD为菱形,
即,解得.
当秒时,四边形AEFD为菱形.
如图2,当时,四边形EBFD为矩形.?
在中,,则,,?
即,?解得.
当时,.
