2020—2021学年人教版数学八年级下册18.2.2菱形课件(共19张ppt)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册18.2.2菱形课件(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 310.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
特殊的平行四边形
菱形
平行
四边形
矩形
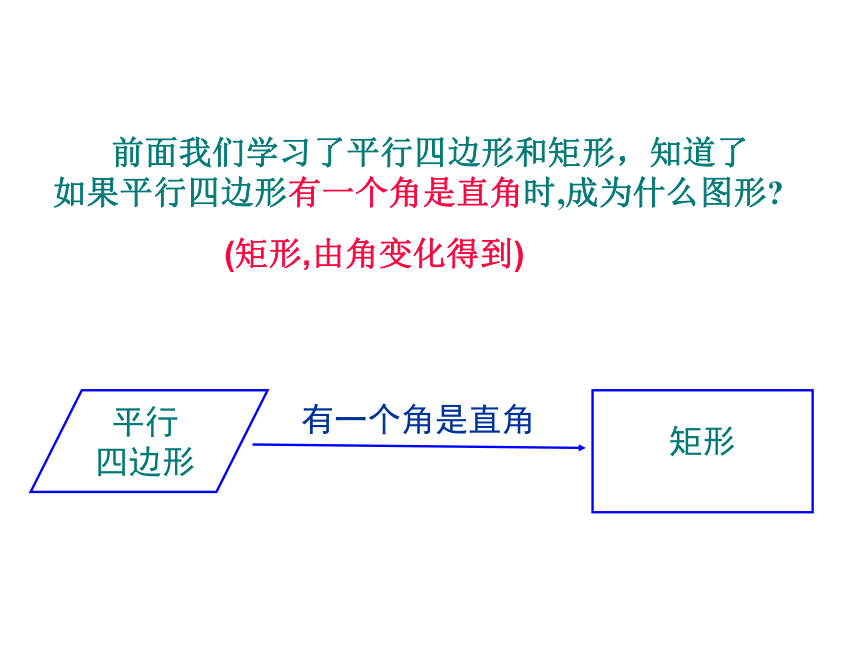
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?
有一个角是直角
(矩形,由角变化得到)
思考
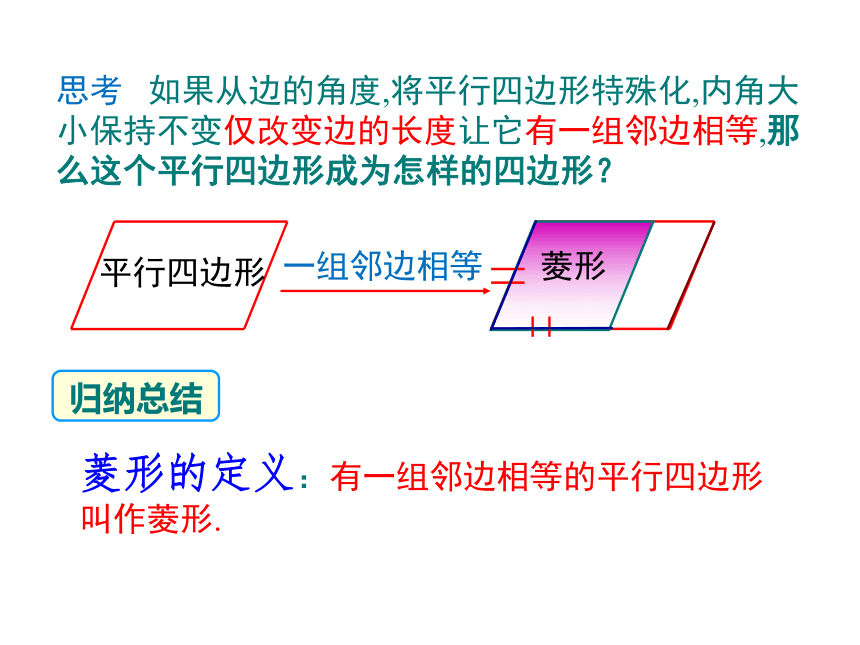
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,那么这个平行四边形成为怎样的四边形?
平行四边形
菱形的定义:有一组邻边相等的平行四边形叫作菱形.
菱形
一组邻边相等
归纳总结
菱形就在我们身边
三菱汽车标志欣赏
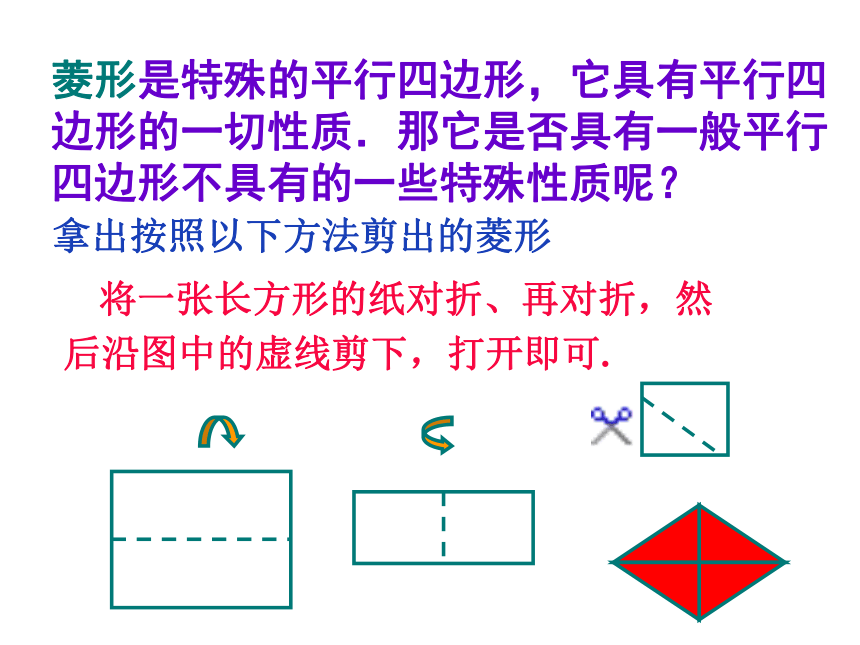
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.
拿出按照以下方法剪出的菱形
菱形是特殊的平行四边形,它具有平行四边形的一切性质.那它是否具有一般平行四边形不具有的一些特殊性质呢?
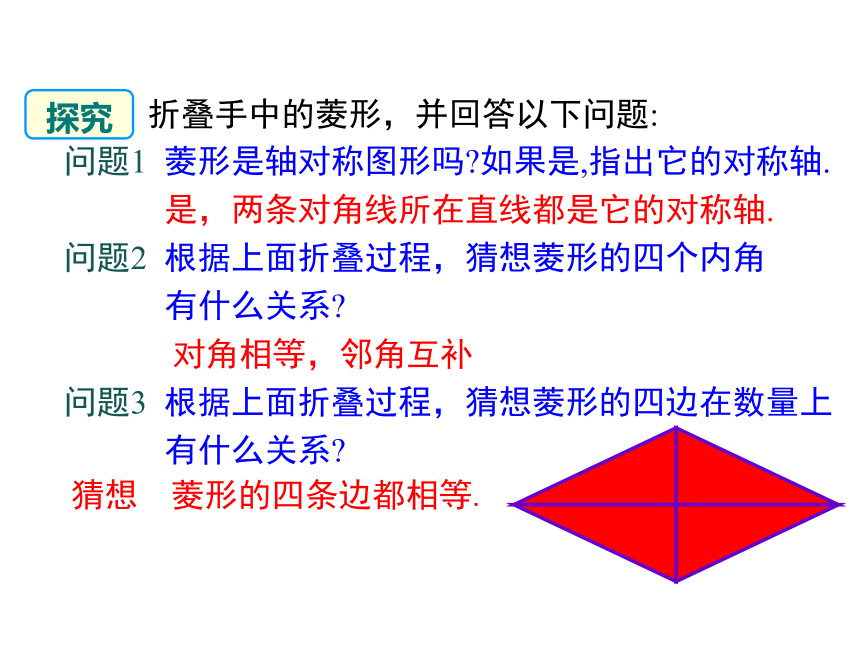
折叠手中的菱形,并回答以下问题:
问题1
菱形是轴对称图形吗?如果是,指出它的对称轴.
是,两条对角线所在直线都是它的对称轴.
问题2
根据上面折叠过程,猜想菱形的四个内角
有什么关系?
对角相等,邻角互补
问题3
根据上面折叠过程,猜想菱形的四边在数量上
有什么关系?
猜想
菱形的四条边都相等.
探究
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:AB
=
BC
=
CD
=AD;
证明:∵四边形ABCD是菱形,
∴AB
=
CD,AD
=
BC.
又∵AB=AD,
∴AB
=
BC
=
CD
=AD.
A
B
C
O
D
证明猜想
菱形的四条边都相等
菱形的性质1
符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
再次折叠手中的图形,并回答以下问题
1.菱形的两对角线有什么关系?
2.对角线分得的每组对角有什么关系?
猜想
菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
探究
已知:如图,在菱形ABCD中求证:AC⊥BD;
AC平分∠BAD和∠BCD
;
BD平分∠ABC和∠ADC
.
A
B
C
O
D
证明:
∵四边形ABCD是菱形,
∴OB
=
OD
.
∵AB
=
AD,
∴AO⊥BD,即AC⊥BD,
AC平分∠BAD.
同理可证AC平分∠BCD
;
BD平分∠ABC
BD平分∠ADC.
证明猜想
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
菱形的性质2
符号语言
∵四边形ABCD是菱形
∴
AC⊥BD
AC平分∠BAD和∠BCD
;
BD平分∠ABC和∠ADC
菱形的性质:
边
菱形的对边平行,四条边都相等
角
菱形的对角线互相垂直且平分,并且每一条对角线都平分一组对角
对角线
菱形的对角相等,邻角互补
总结归纳
对称性
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。
3cm
600
C
C
B
D
A
O
1.已知菱形的周长是12cm,那么它的边长是______.
2.如下图:菱形ABCD中∠BAD=60度,则∠ABD=_______.
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是(
)
A.10cm
B.7cm
C.
5cm
D.4cm
学以致用:
菱形ABCD两条对角线BD、AC长分别是a和b,求菱形的面积。
C
B
D
A
O
你有什么发现?
=
ab
做一做
菱形的面积
=
对角线乘积的一半
菱形的面积
菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积?
A
B
C
D
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
菱形的面积
=
底×高
=
对角线乘积的一半
已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
A
B
C
D
E
O
2
∵四边形ABCD是菱形,
∴AD=AB
解:
∴AD=AB=BD
∵
E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB
的中垂线)
∴
∠DAB=
60
°,
∴
∠ABC=120
°
(2)
∵AE=2,
∴
AB=4
∴
BD=AB=4
∵四边形ABCD是菱形,∴
AC⊥DB
∵
DB=4
∴
0B=2
∴
在R
t△AOB中,由勾股定理得
2
AO=
∴
AC=4
(3)
∴
S菱形ABCD=
×4×4
=8
(1)
对大家说本节课你有哪些收获?
畅所欲言
1个定义
2个公式
3个特性
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形=
对角线乘积的一半
:特在“边、对角线、对称性”
课堂小结
操作题:请把有一个内角为72°的菱形ABCD分成4个等腰三角形.
C
B
)72°
D
A
思考:
特殊的平行四边形
菱形
平行
四边形
矩形
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?
有一个角是直角
(矩形,由角变化得到)
思考
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,那么这个平行四边形成为怎样的四边形?
平行四边形
菱形的定义:有一组邻边相等的平行四边形叫作菱形.
菱形
一组邻边相等
归纳总结
菱形就在我们身边
三菱汽车标志欣赏
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.
拿出按照以下方法剪出的菱形
菱形是特殊的平行四边形,它具有平行四边形的一切性质.那它是否具有一般平行四边形不具有的一些特殊性质呢?
折叠手中的菱形,并回答以下问题:
问题1
菱形是轴对称图形吗?如果是,指出它的对称轴.
是,两条对角线所在直线都是它的对称轴.
问题2
根据上面折叠过程,猜想菱形的四个内角
有什么关系?
对角相等,邻角互补
问题3
根据上面折叠过程,猜想菱形的四边在数量上
有什么关系?
猜想
菱形的四条边都相等.
探究
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:AB
=
BC
=
CD
=AD;
证明:∵四边形ABCD是菱形,
∴AB
=
CD,AD
=
BC.
又∵AB=AD,
∴AB
=
BC
=
CD
=AD.
A
B
C
O
D
证明猜想
菱形的四条边都相等
菱形的性质1
符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
再次折叠手中的图形,并回答以下问题
1.菱形的两对角线有什么关系?
2.对角线分得的每组对角有什么关系?
猜想
菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
探究
已知:如图,在菱形ABCD中求证:AC⊥BD;
AC平分∠BAD和∠BCD
;
BD平分∠ABC和∠ADC
.
A
B
C
O
D
证明:
∵四边形ABCD是菱形,
∴OB
=
OD
.
∵AB
=
AD,
∴AO⊥BD,即AC⊥BD,
AC平分∠BAD.
同理可证AC平分∠BCD
;
BD平分∠ABC
BD平分∠ADC.
证明猜想
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
菱形的性质2
符号语言
∵四边形ABCD是菱形
∴
AC⊥BD
AC平分∠BAD和∠BCD
;
BD平分∠ABC和∠ADC
菱形的性质:
边
菱形的对边平行,四条边都相等
角
菱形的对角线互相垂直且平分,并且每一条对角线都平分一组对角
对角线
菱形的对角相等,邻角互补
总结归纳
对称性
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。
3cm
600
C
C
B
D
A
O
1.已知菱形的周长是12cm,那么它的边长是______.
2.如下图:菱形ABCD中∠BAD=60度,则∠ABD=_______.
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是(
)
A.10cm
B.7cm
C.
5cm
D.4cm
学以致用:
菱形ABCD两条对角线BD、AC长分别是a和b,求菱形的面积。
C
B
D
A
O
你有什么发现?
=
ab
做一做
菱形的面积
=
对角线乘积的一半
菱形的面积
菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积?
A
B
C
D
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
菱形的面积
=
底×高
=
对角线乘积的一半
已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
A
B
C
D
E
O
2
∵四边形ABCD是菱形,
∴AD=AB
解:
∴AD=AB=BD
∵
E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB
的中垂线)
∴
∠DAB=
60
°,
∴
∠ABC=120
°
(2)
∵AE=2,
∴
AB=4
∴
BD=AB=4
∵四边形ABCD是菱形,∴
AC⊥DB
∵
DB=4
∴
0B=2
∴
在R
t△AOB中,由勾股定理得
2
AO=
∴
AC=4
(3)
∴
S菱形ABCD=
×4×4
=8
(1)
对大家说本节课你有哪些收获?
畅所欲言
1个定义
2个公式
3个特性
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形=
对角线乘积的一半
:特在“边、对角线、对称性”
课堂小结
操作题:请把有一个内角为72°的菱形ABCD分成4个等腰三角形.
C
B
)72°
D
A
思考:
