六年级数学下册试题 一课一练《统计与可能性》习题2-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《统计与可能性》习题2-北师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 513.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 14:57:18 | ||
图片预览




文档简介
《统计与可能性》习题2
1、要表示长安区各小学学生占长安区总学生数的百分比情况,用________统计图比较合适.要清楚表示某商场营业额变化情况,应该选用________统计图.
2、下面是林场育苗基地树苗情况统计图
(1)柳树有3500棵,这些树苗的总数是多少棵?
(2)松树和柏树分别有多少棵?
(3)杨树比槐树多百分之几?
3、某市科学考试实施改革,考试结果以等级形式呈现,分A、B、C、D四个等级.某校六年级为了迎接毕业考试,进行了一次模拟考试,随机抽取部分学生的科学成绩进行调查统计,绘制成如图所示两幅不完整的统计图.
(1)这次调查共抽取了________名学生的科学成绩.
(2)扇形统计图中,D等级所对应的扇形中,以圆心为顶点的角的度数为________度.
(3)将条形统计图补充完整.
(4)如果该校六年级共有500名学生,估计一下这次模拟考试有________名学生的科学成绩等级为D.
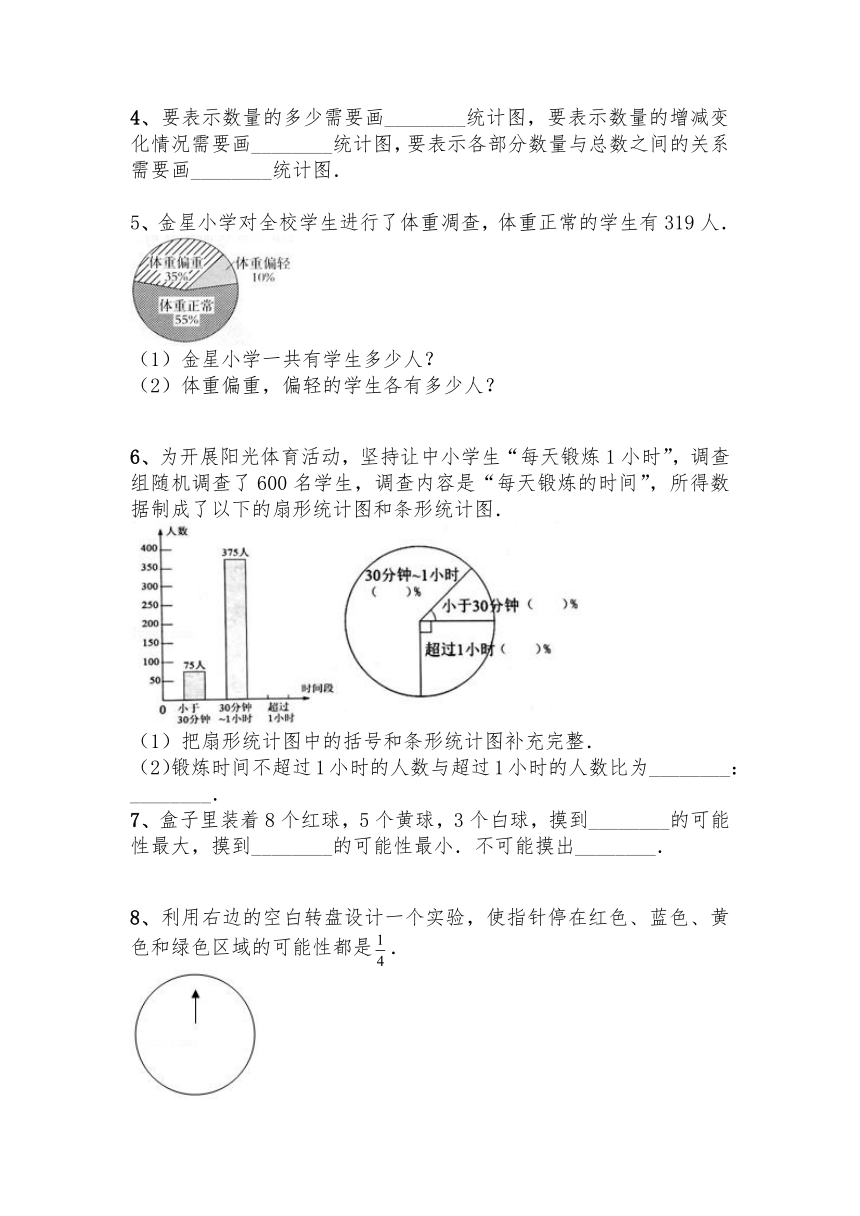
4、要表示数量的多少需要画________统计图,要表示数量的增减变化情况需要画________统计图,要表示各部分数量与总数之间的关系需要画________统计图.
5、金星小学对全校学生进行了体重凋查,体重正常的学生有319人.
(1)金星小学一共有学生多少人?
(2)体重偏重,偏轻的学生各有多少人?
6、为开展阳光体育活动,坚持让中小学生“每天锻炼1小时”,调查组随机调查了600名学生,调查内容是“每天锻炼的时间”,所得数据制成了以下的扇形统计图和条形统计图.
(1)把扇形统计图中的括号和条形统计图补充完整.
(2)锻炼时间不超过1小时的人数与超过1小时的人数比为________:________.
7、盒子里装着8个红球,5个黄球,3个白球,摸到________的可能性最大,摸到________的可能性最小.不可能摸出________.
8、利用右边的空白转盘设计一个实验,使指针停在红色、蓝色、黄色和绿色区域的可能性都是.
9、投掷100次硬币,有48次正面向上,那么投掷第101次硬币正面向上的可能性是________.
10、掷一枚正方体的骰子,朝上一面的点数为素数的可能性大小是________.
11、一副扑克牌,去掉大、小王,从中任意摸一张,摸到K的可能性是________,摸到方块的可能性是________.
12、盒子里放了4个乒乓球,分别标着1、2、3、4四个号码,从中任意摸出2个球,有________种可能的结果.
13、动手动脑连一连:
14、填一填、画一画:下面每个转盘有红、黄、蓝三种颜色,前两个转盘的指针停在哪种颜色的可能性大?请你再设计一个转盘,使指针停在红色部分的可能性最大,停在黄、蓝两种颜色的可能性差不多.
15、墨莫投掷硬币,前10次投掷情况为7次正面朝上,3次反面朝上.现在墨莫再投掷一次的话,这次正面朝上的可能性为________(填分数).
16、一个骰子上分别标有1、2、3、4、5、6,掷这个骰子,单数朝上的可能性是________,双数朝上的可能性是________.“1”朝上的可能性是________.
17、悠悠拿出一副扑克牌,去掉了大王和小王,把扑克牌背面朝上放在桌上.从这些扑克中任意抽出一张,是红色的可能性是________,是梅花的可能性是________,是的可能性是________,是红桃10的可能性是________.
18、一个袋子中装有3个白球,2个黄球和1个黑球.如果小东从袋子中任意摸出2个球,摸出的2个球可能是什么球,请列举出来.
19、按要求涂一涂(提示:用彩笔).
(1)指针可能停在红色、黄色和蓝色区域,停在黄色区域的可能性最大,停在蓝色区域的可能性最小.
(2)指针可能停在红色、黄色和蓝色区域,停在红色和黄色区域的可能性一样大,停在蓝色区域的可能性较小.
20、在一个袋子中装有同一种形状的20粒纽扣,其中黑的有6粒,蓝的有4粒,红的有10粒.(如图)
(1)摸出1粒时,可能出现哪几种结果?列举出来.
(2)摸出1粒时,摸到哪种颜色纽扣的可能性最大?
(3)摸出11粒时,其中一定有什么颜色的?
21、四(2)班新校服到了,班长李想抱着校服往班上跑,一不小心把4套男式校服和2套女式校服掉在了地上.他随手捡起3套,可能有几种情况?可能性最大的是哪一种情况?
22、聪聪和明明下军棋,用摸扑克牌来决定由谁先出棋.他们选了四张扑克牌,其中两张是红桃,另两张是黑桃.将四张扑克牌背面朝上,每人摸出一张,如果两人摸出的牌颜色相同,则小平先出棋;如果颜色不同则小玲先出棋.请回答下列问题:
(1)摸出两张牌是同样颜色的可能性是________.
(2)摸出两张牌是不同样颜色的可能性是________.
(3)这个游戏规则公平吗?________.
23、转动转盘,待转盘停下后,指针指向红色区域要唱歌,指向绿色区域要跳舞,指向橙色区域要讲故事.
(1)转动转盘,指针可能停在________色区域,也可能停在________色区域,指针停在________色区域的可能性大,停在________色区域的可能性小.
(2)乐乐想要唱歌,她最好选择使用________转盘.
(3)小然不会跳舞,她最好选择使用________转盘.
24、一把钥匙只能开一把锁,现在有5把钥匙和5把锁,但不知道哪把钥匙配哪把锁,那么最多要试多少次才能配好所有的钥匙和锁?
25、小红和小刚做游戏,他们一人从卡片1、6、3、8中任意抽取两张,如果他们的和是单数则小红获胜,如果他们的和是双数,则小刚获胜.这个玩法公平吗?你能换一张卡片使游戏公平吗?
26、国庆节期间,便民超市举办有奖销售活动.顾客购物满100元即可参加摸奖活动.下面两个箱子放有①~⑥号乒乓球各10个,摸奖公告如下:
(1)王阿姨正在摸奖,请你猜一猜她最有可能获得什么?
(2)小明说:“这次摸一等奖的可能性比摸二等奖的可能性大.”你认为他说得对吗?为什么?
答案
1、扇形;折线
2、(1)(棵)
答:这些树苗的总数是14000棵.
(2)(棵),(棵)
答:松树有2100棵,柏树有1400棵.
(3)
答:杨树比槐树多约.
3、(1)15÷30%=50(名)
答:这次调查共抽取了50名学生的科学成绩.
(2)D等级人数为:50-15-22-8=5(名)
360°=36°
答:扇形统计图中,D等级所对应的扇形中,以圆心为顶点的角的度数为36度.
(3)如图所示:
(4)50050(人)
答:如果该校六年级共有500名学生,估计一下这次模拟考试有50名学生的科学成绩等级为D.
4、条形;折线;扇形
5、(1)(人),
答:金星小学一共有学生580人.
(2)(人),(人),
答:体重偏重的学生有203人,体重偏轻的学生有58人.
6、(1)600-75-375=150(人)
75÷600=12.5%
375÷600=62.5%
150÷600=25%
如图:
(2)600-150=450(人),450:150=1:3
答:锻炼时间不超过1小时的人数与超过1小时的人数比为1:3.
7、红球;白球;黑球
8、将转盘平均分成4份,使红色和蓝色、黄色、绿色区域各占其中的一份;如下图:
9、
10、
11、;
12、6
13、
14、;蓝色;黄色
15、
16、;;
17、;;;
18、任意摸出2个球,可能有以下5种情况
2个白球;2个黄球;1个白球、1个黄球;1个白球、1个黑球;1个黄球、1个黑球
19、如图:
20、(1)因为袋子中有3种颜色的纽扣,可得:摸出1粒时,可能出现哪3种结果,黑、蓝、红;
(2)10>6>4,所以摸出1粒时,摸到红色颜色纽扣的可能性最大;
(3)假设前10个都摸出黑和蓝色的纽扣,再摸出1个一定就是红色纽扣,摸出11粒时,其中一定有红颜色的纽扣.
21、他刚捡起3套,可能有以下3种情况
1、3套男式
2、2套男式,1套女式
3、1套男式,2套女式
可能行最大的是捡起3套校服有2套男式,1套女式
22、(1)因为两张红桃,两张黑桃一共的组合方式有:4×3÷2=6(种),
其中摸出同色的组合只有红红和黑黑两种,
所以:;
(2);
(3)因为摸出两张牌是同样颜色的可能性和摸出两张牌是不同样颜色的可能性不相等,即;
所以这个游戏规则不公平.
23、(1)转动转盘,指针可能停在
红色区域,也可能停在
绿色区域,指针停在
红色区域的可能性大,停在
绿色区域的可能性小.
(2)乐乐想要唱歌,她最好选择使用转盘.
(3)小然不会跳舞,她最好选择使用转盘.
24、如上图,先试第1把锁,有5把钥匙,最多要试4次,就可以确定跟第1把锁配对的钥匙;
再试第2把锁,有4把钥匙,最多需要试3次,就可以确定跟第2把锁配对的钥匙;
试第3把锁,有3把钥匙,最多需要试2次,就可以确定跟第3把锁配对的钥匙;
试第4把锁,有2把钥匙,最多需要试1次,就可以确定跟第4把锁配对的钥匙;
最后只剩下第5把锁和一把钥匙,即为配对的一组。
4+3+2+1=10(次)
故:最多要试10次才能配好所有的钥匙和锁。
25、从卡片1、6、3、8中任意抽取两张,组成的和有:1与6、3、8的和分别是7、4、9;6与3、8的和分别是:9、14;3与8的和是11;一共6种情况,
和是双数的有4、14两种情况,可能性是:;
和是单数的有7、9、9、11,四种情况,可能性是:;
因为它们的可能性不相同,所以这个玩法不公平;
要使游戏公平,可以把其中一张单数的卡片换成双数,这样根据单数与双数的和的特点即可得出它们的和有3个单数3个双数.
26、(1)最有可能获得抽纸一盒
(2)不对.因为和是2或12比和是3或11的次数少,所以摸一等奖的可能性比摸二等奖的可能性小
1、要表示长安区各小学学生占长安区总学生数的百分比情况,用________统计图比较合适.要清楚表示某商场营业额变化情况,应该选用________统计图.
2、下面是林场育苗基地树苗情况统计图
(1)柳树有3500棵,这些树苗的总数是多少棵?
(2)松树和柏树分别有多少棵?
(3)杨树比槐树多百分之几?
3、某市科学考试实施改革,考试结果以等级形式呈现,分A、B、C、D四个等级.某校六年级为了迎接毕业考试,进行了一次模拟考试,随机抽取部分学生的科学成绩进行调查统计,绘制成如图所示两幅不完整的统计图.
(1)这次调查共抽取了________名学生的科学成绩.
(2)扇形统计图中,D等级所对应的扇形中,以圆心为顶点的角的度数为________度.
(3)将条形统计图补充完整.
(4)如果该校六年级共有500名学生,估计一下这次模拟考试有________名学生的科学成绩等级为D.
4、要表示数量的多少需要画________统计图,要表示数量的增减变化情况需要画________统计图,要表示各部分数量与总数之间的关系需要画________统计图.
5、金星小学对全校学生进行了体重凋查,体重正常的学生有319人.
(1)金星小学一共有学生多少人?
(2)体重偏重,偏轻的学生各有多少人?
6、为开展阳光体育活动,坚持让中小学生“每天锻炼1小时”,调查组随机调查了600名学生,调查内容是“每天锻炼的时间”,所得数据制成了以下的扇形统计图和条形统计图.
(1)把扇形统计图中的括号和条形统计图补充完整.
(2)锻炼时间不超过1小时的人数与超过1小时的人数比为________:________.
7、盒子里装着8个红球,5个黄球,3个白球,摸到________的可能性最大,摸到________的可能性最小.不可能摸出________.
8、利用右边的空白转盘设计一个实验,使指针停在红色、蓝色、黄色和绿色区域的可能性都是.
9、投掷100次硬币,有48次正面向上,那么投掷第101次硬币正面向上的可能性是________.
10、掷一枚正方体的骰子,朝上一面的点数为素数的可能性大小是________.
11、一副扑克牌,去掉大、小王,从中任意摸一张,摸到K的可能性是________,摸到方块的可能性是________.
12、盒子里放了4个乒乓球,分别标着1、2、3、4四个号码,从中任意摸出2个球,有________种可能的结果.
13、动手动脑连一连:
14、填一填、画一画:下面每个转盘有红、黄、蓝三种颜色,前两个转盘的指针停在哪种颜色的可能性大?请你再设计一个转盘,使指针停在红色部分的可能性最大,停在黄、蓝两种颜色的可能性差不多.
15、墨莫投掷硬币,前10次投掷情况为7次正面朝上,3次反面朝上.现在墨莫再投掷一次的话,这次正面朝上的可能性为________(填分数).
16、一个骰子上分别标有1、2、3、4、5、6,掷这个骰子,单数朝上的可能性是________,双数朝上的可能性是________.“1”朝上的可能性是________.
17、悠悠拿出一副扑克牌,去掉了大王和小王,把扑克牌背面朝上放在桌上.从这些扑克中任意抽出一张,是红色的可能性是________,是梅花的可能性是________,是的可能性是________,是红桃10的可能性是________.
18、一个袋子中装有3个白球,2个黄球和1个黑球.如果小东从袋子中任意摸出2个球,摸出的2个球可能是什么球,请列举出来.
19、按要求涂一涂(提示:用彩笔).
(1)指针可能停在红色、黄色和蓝色区域,停在黄色区域的可能性最大,停在蓝色区域的可能性最小.
(2)指针可能停在红色、黄色和蓝色区域,停在红色和黄色区域的可能性一样大,停在蓝色区域的可能性较小.
20、在一个袋子中装有同一种形状的20粒纽扣,其中黑的有6粒,蓝的有4粒,红的有10粒.(如图)
(1)摸出1粒时,可能出现哪几种结果?列举出来.
(2)摸出1粒时,摸到哪种颜色纽扣的可能性最大?
(3)摸出11粒时,其中一定有什么颜色的?
21、四(2)班新校服到了,班长李想抱着校服往班上跑,一不小心把4套男式校服和2套女式校服掉在了地上.他随手捡起3套,可能有几种情况?可能性最大的是哪一种情况?
22、聪聪和明明下军棋,用摸扑克牌来决定由谁先出棋.他们选了四张扑克牌,其中两张是红桃,另两张是黑桃.将四张扑克牌背面朝上,每人摸出一张,如果两人摸出的牌颜色相同,则小平先出棋;如果颜色不同则小玲先出棋.请回答下列问题:
(1)摸出两张牌是同样颜色的可能性是________.
(2)摸出两张牌是不同样颜色的可能性是________.
(3)这个游戏规则公平吗?________.
23、转动转盘,待转盘停下后,指针指向红色区域要唱歌,指向绿色区域要跳舞,指向橙色区域要讲故事.
(1)转动转盘,指针可能停在________色区域,也可能停在________色区域,指针停在________色区域的可能性大,停在________色区域的可能性小.
(2)乐乐想要唱歌,她最好选择使用________转盘.
(3)小然不会跳舞,她最好选择使用________转盘.
24、一把钥匙只能开一把锁,现在有5把钥匙和5把锁,但不知道哪把钥匙配哪把锁,那么最多要试多少次才能配好所有的钥匙和锁?
25、小红和小刚做游戏,他们一人从卡片1、6、3、8中任意抽取两张,如果他们的和是单数则小红获胜,如果他们的和是双数,则小刚获胜.这个玩法公平吗?你能换一张卡片使游戏公平吗?
26、国庆节期间,便民超市举办有奖销售活动.顾客购物满100元即可参加摸奖活动.下面两个箱子放有①~⑥号乒乓球各10个,摸奖公告如下:
(1)王阿姨正在摸奖,请你猜一猜她最有可能获得什么?
(2)小明说:“这次摸一等奖的可能性比摸二等奖的可能性大.”你认为他说得对吗?为什么?
答案
1、扇形;折线
2、(1)(棵)
答:这些树苗的总数是14000棵.
(2)(棵),(棵)
答:松树有2100棵,柏树有1400棵.
(3)
答:杨树比槐树多约.
3、(1)15÷30%=50(名)
答:这次调查共抽取了50名学生的科学成绩.
(2)D等级人数为:50-15-22-8=5(名)
360°=36°
答:扇形统计图中,D等级所对应的扇形中,以圆心为顶点的角的度数为36度.
(3)如图所示:
(4)50050(人)
答:如果该校六年级共有500名学生,估计一下这次模拟考试有50名学生的科学成绩等级为D.
4、条形;折线;扇形
5、(1)(人),
答:金星小学一共有学生580人.
(2)(人),(人),
答:体重偏重的学生有203人,体重偏轻的学生有58人.
6、(1)600-75-375=150(人)
75÷600=12.5%
375÷600=62.5%
150÷600=25%
如图:
(2)600-150=450(人),450:150=1:3
答:锻炼时间不超过1小时的人数与超过1小时的人数比为1:3.
7、红球;白球;黑球
8、将转盘平均分成4份,使红色和蓝色、黄色、绿色区域各占其中的一份;如下图:
9、
10、
11、;
12、6
13、
14、;蓝色;黄色
15、
16、;;
17、;;;
18、任意摸出2个球,可能有以下5种情况
2个白球;2个黄球;1个白球、1个黄球;1个白球、1个黑球;1个黄球、1个黑球
19、如图:
20、(1)因为袋子中有3种颜色的纽扣,可得:摸出1粒时,可能出现哪3种结果,黑、蓝、红;
(2)10>6>4,所以摸出1粒时,摸到红色颜色纽扣的可能性最大;
(3)假设前10个都摸出黑和蓝色的纽扣,再摸出1个一定就是红色纽扣,摸出11粒时,其中一定有红颜色的纽扣.
21、他刚捡起3套,可能有以下3种情况
1、3套男式
2、2套男式,1套女式
3、1套男式,2套女式
可能行最大的是捡起3套校服有2套男式,1套女式
22、(1)因为两张红桃,两张黑桃一共的组合方式有:4×3÷2=6(种),
其中摸出同色的组合只有红红和黑黑两种,
所以:;
(2);
(3)因为摸出两张牌是同样颜色的可能性和摸出两张牌是不同样颜色的可能性不相等,即;
所以这个游戏规则不公平.
23、(1)转动转盘,指针可能停在
红色区域,也可能停在
绿色区域,指针停在
红色区域的可能性大,停在
绿色区域的可能性小.
(2)乐乐想要唱歌,她最好选择使用转盘.
(3)小然不会跳舞,她最好选择使用转盘.
24、如上图,先试第1把锁,有5把钥匙,最多要试4次,就可以确定跟第1把锁配对的钥匙;
再试第2把锁,有4把钥匙,最多需要试3次,就可以确定跟第2把锁配对的钥匙;
试第3把锁,有3把钥匙,最多需要试2次,就可以确定跟第3把锁配对的钥匙;
试第4把锁,有2把钥匙,最多需要试1次,就可以确定跟第4把锁配对的钥匙;
最后只剩下第5把锁和一把钥匙,即为配对的一组。
4+3+2+1=10(次)
故:最多要试10次才能配好所有的钥匙和锁。
25、从卡片1、6、3、8中任意抽取两张,组成的和有:1与6、3、8的和分别是7、4、9;6与3、8的和分别是:9、14;3与8的和是11;一共6种情况,
和是双数的有4、14两种情况,可能性是:;
和是单数的有7、9、9、11,四种情况,可能性是:;
因为它们的可能性不相同,所以这个玩法不公平;
要使游戏公平,可以把其中一张单数的卡片换成双数,这样根据单数与双数的和的特点即可得出它们的和有3个单数3个双数.
26、(1)最有可能获得抽纸一盒
(2)不对.因为和是2或12比和是3或11的次数少,所以摸一等奖的可能性比摸二等奖的可能性小
