2020-2021学年人教版数学八年级下册18.2.3.2:特殊平行四边形性质、判定综合应用课件(共18张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.2.3.2:特殊平行四边形性质、判定综合应用课件(共18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 147.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
特殊平行四边形
性质、判定的综合运用
知识回顾:
我们学习了几种特殊的平行四边形?
1、定义是什么?
2、判定分别是什么?
观看:几何画板动画演示
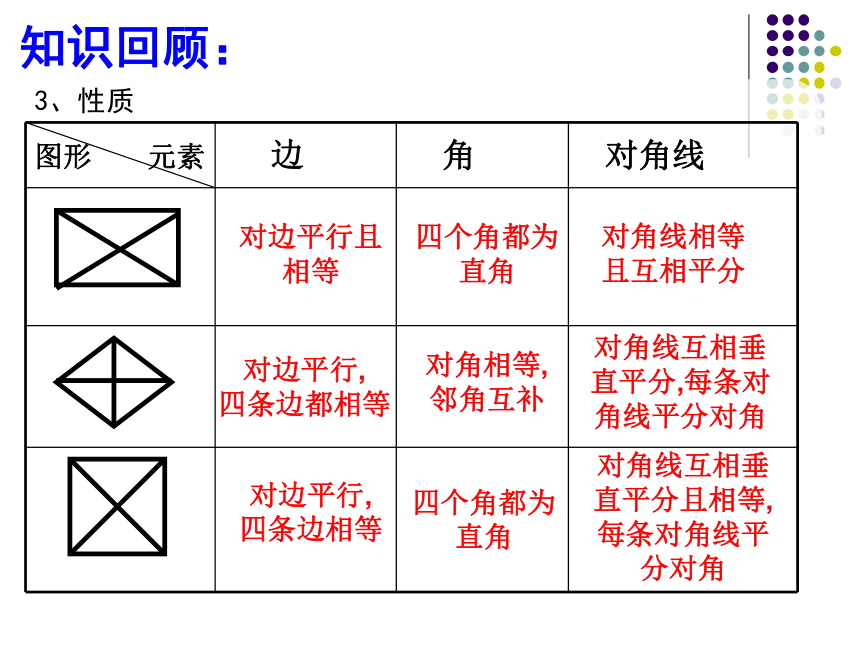
知识回顾:
图形
元素
边
角
对角线
对边平行且相等
对边平行,
四条边都相等
对边平行,
四条边相等
四个角都为直角
对角相等,
邻角互补
四个角都为直角
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分对角
对角线互相垂直平分且相等,
每条对角线平分对角
3、性质
知识点强调:
①矩形和菱形是特殊的平行四边形,具备平行四边形的所有性质;
②正方形既是矩形也是菱形,它具备矩形和菱形的所有性质。
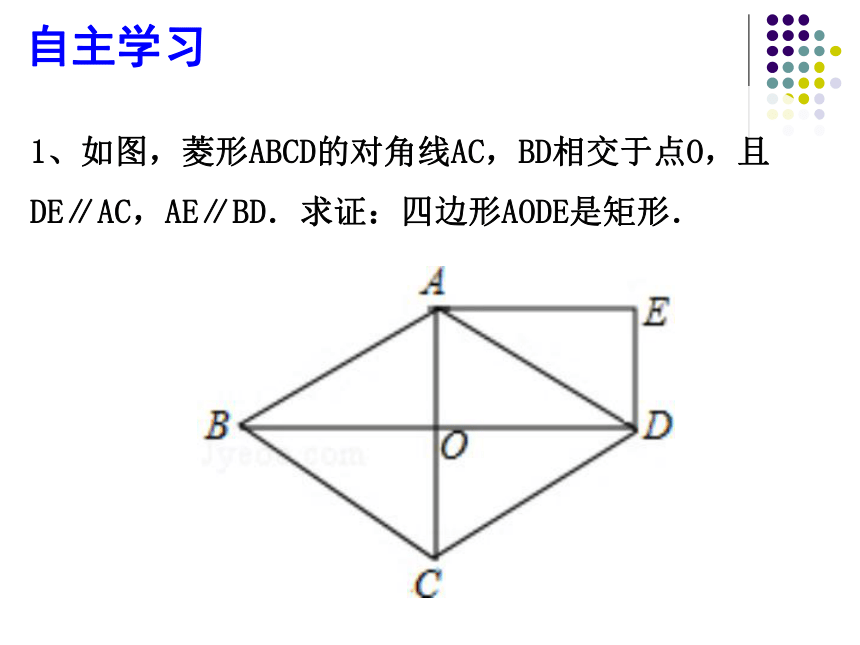
自主学习
1、如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.
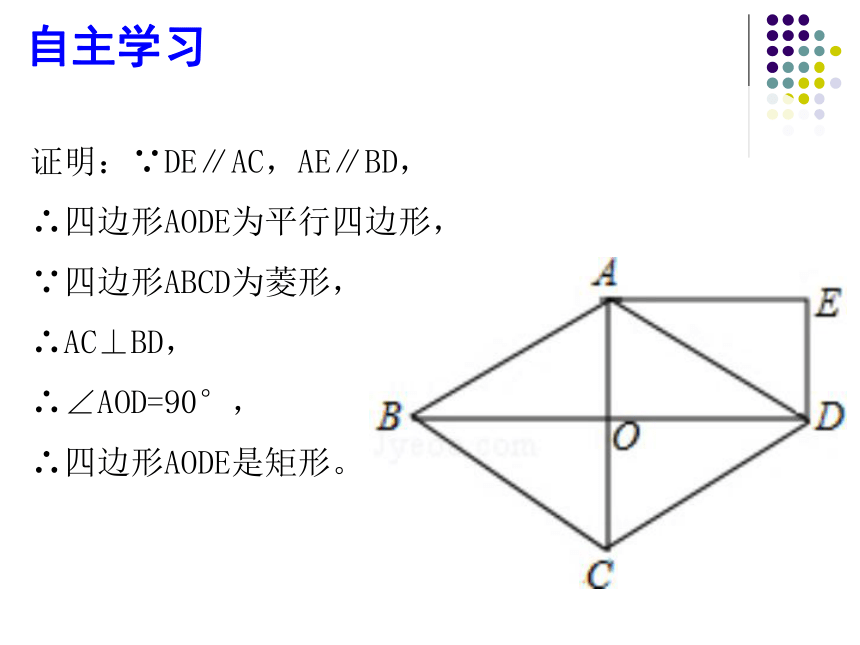
自主学习
证明:∵DE∥AC,AE∥BD,
∴四边形AODE为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形。
方法小结:
证明四边形是特殊的平行四边形的方法:(1)先由已知条件确定判定方法
(2)
利用已知图形性质推导出判定条件。
动手操作:
2、如图,小强拿一张正方形的纸(图(1)),沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线剪成两部分,再把所得的三角形的部分打开后的形状一定是(
)
A.一般的平行四边形
B、菱形
C、矩形
D、正方形
(1)
(2)
B
(3)
小组合作探究
教科书中第69页第14题:
3、如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
求证:AE=EF
H
G
证明过程:
证明:取AB的中点G,连接EG,
∵四边形ABCD为正方形,
∴AB=BC,∠ABE=∠BCD=90°
∵E,G分别是AB,BC的中点,
∴AG=BG=
AB
EC=BE=
BC
∴AG=EC
BG=BE
∴∠BGE=∠BEG=45°,
∴∠AGE=1800-450=135°,
∵CF平分∠DCH,
∴∠FCH=
∠DCH=
45°,
∴∠ECF=1800-450=135°,
∴∠ECF=∠AGE
H
G
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
又∵∠GAE+∠AEB=90°,∴∠GAE=∠FEC,∴△AGE≌△ECF(ASA),∴AE=EF
4、如图(2),四边形ABCD是正方形,点E为BC反向延长线上一点,∠AEF=90°,且EF交正方形外角的平分线CM所在直线于点F.求证:AE=EF.
进一步探究
G
H
证明过程:
证明
:在AB延长线上截取BG=BE,连接EG.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°.
又∵BG=BE,
∴AG=CE.
∵∠ABC=∠BCD=90°,BG=BE,∴∠AGE=∠BEG=45°
∵CM为正方形外角平分线
∴∠ECF=∠MCH=45°∴∠AGE=∠ECF=45°
证明过程:
∵∠ABE=90°,∠AEF=90°
∴∠AEB+∠EAG=90°,∠AEB+∠FEC=90°
∴∠EAG=∠FEC
又AG=CE,∠AGE=∠ECF,
在△EAG和△FEC中,
∠EAG=∠FEC,AG=CE,∠AGE=∠ECF,
∴△EAG≌△FEC(ASA),
∴AE=EF.
方法小结:
证明线段相等的方法:
一般通过证明线段所在三角形全等,所在三角形若不能全等,可以考虑重新构造三角形。
课堂总结:
谈谈这节课你的收获:
1、会运用判定定理证明一个四边形是矩形、菱形、正方形。
2、会灵活运用性质定理综合解题。
作业布置:
1、复习特殊平行四边形的性质和判定;
2、巩固本节课:完成课后习题。
课后作业:
如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
图1
谢谢!
特殊平行四边形
性质、判定的综合运用
知识回顾:
我们学习了几种特殊的平行四边形?
1、定义是什么?
2、判定分别是什么?
观看:几何画板动画演示
知识回顾:
图形
元素
边
角
对角线
对边平行且相等
对边平行,
四条边都相等
对边平行,
四条边相等
四个角都为直角
对角相等,
邻角互补
四个角都为直角
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分对角
对角线互相垂直平分且相等,
每条对角线平分对角
3、性质
知识点强调:
①矩形和菱形是特殊的平行四边形,具备平行四边形的所有性质;
②正方形既是矩形也是菱形,它具备矩形和菱形的所有性质。
自主学习
1、如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.
自主学习
证明:∵DE∥AC,AE∥BD,
∴四边形AODE为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形。
方法小结:
证明四边形是特殊的平行四边形的方法:(1)先由已知条件确定判定方法
(2)
利用已知图形性质推导出判定条件。
动手操作:
2、如图,小强拿一张正方形的纸(图(1)),沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线剪成两部分,再把所得的三角形的部分打开后的形状一定是(
)
A.一般的平行四边形
B、菱形
C、矩形
D、正方形
(1)
(2)
B
(3)
小组合作探究
教科书中第69页第14题:
3、如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
求证:AE=EF
H
G
证明过程:
证明:取AB的中点G,连接EG,
∵四边形ABCD为正方形,
∴AB=BC,∠ABE=∠BCD=90°
∵E,G分别是AB,BC的中点,
∴AG=BG=
AB
EC=BE=
BC
∴AG=EC
BG=BE
∴∠BGE=∠BEG=45°,
∴∠AGE=1800-450=135°,
∵CF平分∠DCH,
∴∠FCH=
∠DCH=
45°,
∴∠ECF=1800-450=135°,
∴∠ECF=∠AGE
H
G
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
又∵∠GAE+∠AEB=90°,∴∠GAE=∠FEC,∴△AGE≌△ECF(ASA),∴AE=EF
4、如图(2),四边形ABCD是正方形,点E为BC反向延长线上一点,∠AEF=90°,且EF交正方形外角的平分线CM所在直线于点F.求证:AE=EF.
进一步探究
G
H
证明过程:
证明
:在AB延长线上截取BG=BE,连接EG.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°.
又∵BG=BE,
∴AG=CE.
∵∠ABC=∠BCD=90°,BG=BE,∴∠AGE=∠BEG=45°
∵CM为正方形外角平分线
∴∠ECF=∠MCH=45°∴∠AGE=∠ECF=45°
证明过程:
∵∠ABE=90°,∠AEF=90°
∴∠AEB+∠EAG=90°,∠AEB+∠FEC=90°
∴∠EAG=∠FEC
又AG=CE,∠AGE=∠ECF,
在△EAG和△FEC中,
∠EAG=∠FEC,AG=CE,∠AGE=∠ECF,
∴△EAG≌△FEC(ASA),
∴AE=EF.
方法小结:
证明线段相等的方法:
一般通过证明线段所在三角形全等,所在三角形若不能全等,可以考虑重新构造三角形。
课堂总结:
谈谈这节课你的收获:
1、会运用判定定理证明一个四边形是矩形、菱形、正方形。
2、会灵活运用性质定理综合解题。
作业布置:
1、复习特殊平行四边形的性质和判定;
2、巩固本节课:完成课后习题。
课后作业:
如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
图1
谢谢!
