2020-2021学年八年级数学北师大版下册 第三章 3.3.2 中心对称图形 课件(共58张PPT)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第三章 3.3.2 中心对称图形 课件(共58张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 20:23:04 | ||
图片预览








文档简介
(共58张PPT)
第三章
图形的平移与旋转
3.1.2
中心对称图形
北师大版数学八年级下册
学习目标
1.了解中心对称图形的概念,以及两个图形成中心对称和中心对称图形的关系。
2.初步学会识别常见的中心对称图形或图案,并能用推理方式说明一个图形是中心对称图形。
我们上节课学习了中心对称的相关知识,中心对称是指两个图形的关系,而把这两个图形看作一个整体是什么图形呢?是我们这节课所要学习的中心对称图形.
导入新知
1
知识点
中心对称图形的定义
(1)如图,将线段AB绕它的中点旋转180°,你
有什么发现?
A
B
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
问
题
合作探究
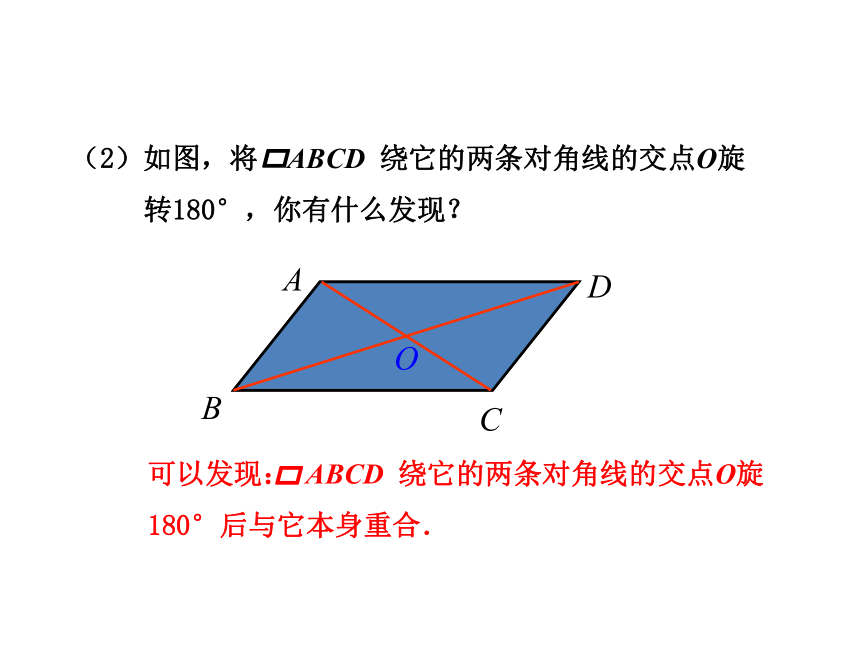
(2)如图,将
ABCD
绕它的两条对角线的交点O旋
转180°,你有什么发现?
A
B
C
D
O
可以发现:
ABCD
绕它的两条对角线的交点O旋180°后与它本身重合.
像这样,把一个图形绕着某一个点旋转180°,
如果旋转后的图形能够与原来的图形重合,那么这
个图形叫做中心对称图形
这个点就是它的对称中心.
新知小结
中心对称与中心对称图形的区别与联系
:
中心对称
中心对称图形
区别
(1)是针对2个图形而言的
(2)是指两个图形的(位置)
关系
(3)对称点在两个图形上
(4)对称中心在两个图形之
间
(1)是针对1个图形而言的
(2)是指具有某种性质的一
个图形
(3)对称点在一个图形上
(4)对称中心在图形上或其
内部
联系
若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
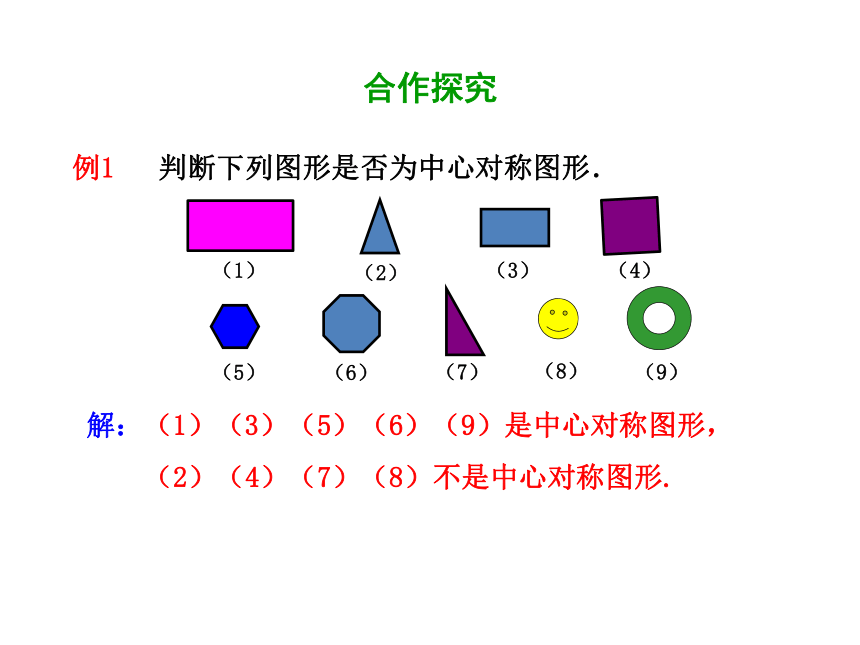
例1
判断下列图形是否为中心对称图形.
解:(1)(3)(5)(6)(9)是中心对称图形,
(2)(4)(7)(8)不是中心对称图形.
(1)
(9)
(8)
(7)
(6)
(5)
(4)
(3)
(2)
合作探究
正多边形图案为中心对称图形的识别方法:边数为偶数的正多边形图案是中心对称图形,相应地,与边数为偶数的正多边形具有类似的特征的图形是中心对称图形;边数为奇数的正多边形或具有类似的特征的图形一定不是中心对称图形.
新知小结
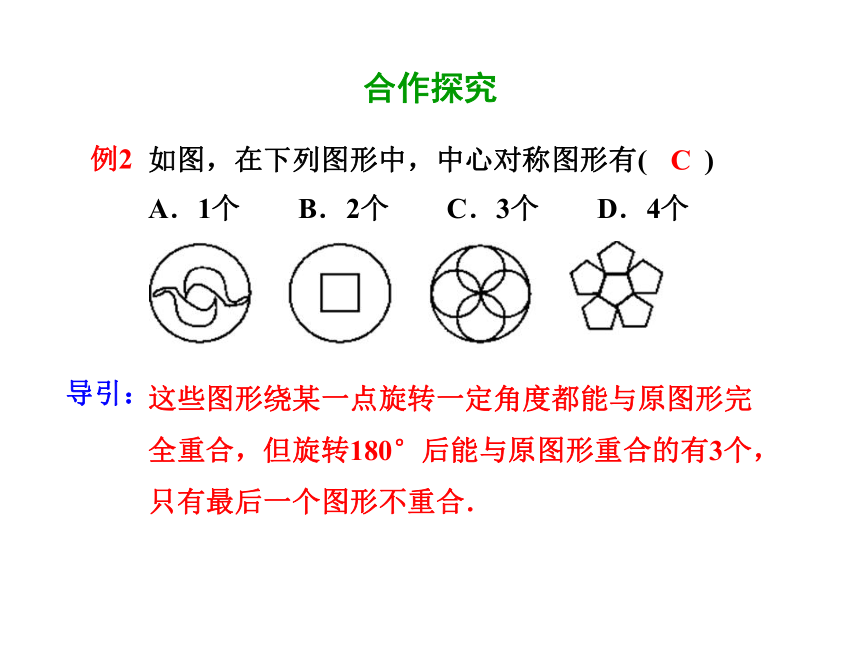
如图,在下列图形中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
例2
导引:
这些图形绕某一点旋转一定角度都能与原图形完
全重合,但旋转180°后能与原图形重合的有3个,
只有最后一个图形不重合.
C
合作探究
正多边形图案是否为中心对称图形的识别方法:
边数为偶数的正多边形图案是中心对称图形,
相应地,与边数为偶数的正多边形具有类似的特
征的图形是中心对称图形;边数为奇数的正多边
形或具有类似的特征的图形一定不是中心对称图
形.
新知小结
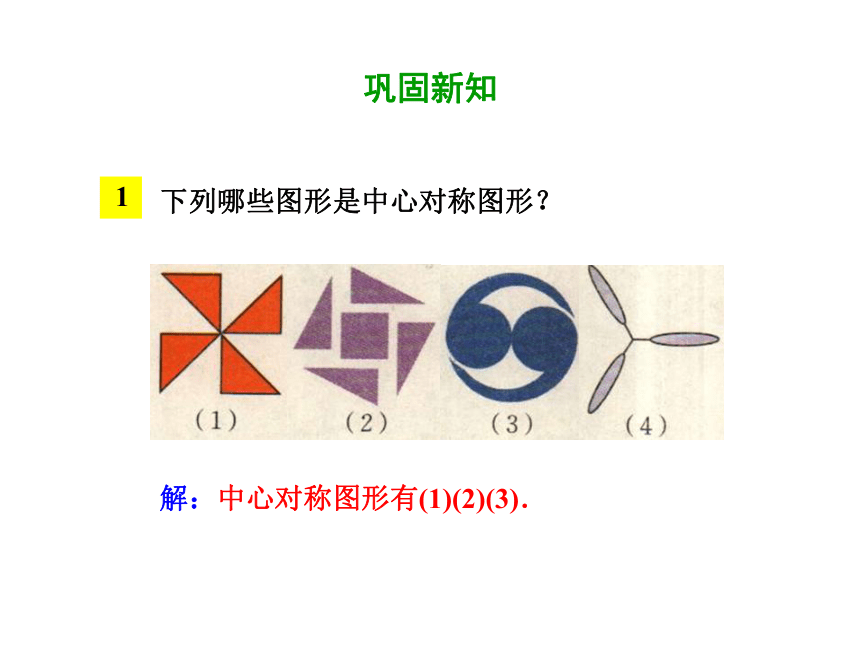
下列哪些图形是中心对称图形?
1
解:中心对称图形有(1)(2)(3).
巩固新知
下面扑克牌中,哪些牌的牌面是中心对称图形?
2
解:第一张和第三张牌的牌面是中心对称图形.
【中考·玉林、崇左】五星红旗的每个五星( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
3
A
【中考·自贡】下列图形中,是轴对称图形,但不是中心对称图形的是( )
4
A
【中考·攀枝花】下列图形中,既是轴对称图形又是中心对称图形的是( )
5
D
如图,对其对称性描述正确的是( )
A.是轴对称图形
B.是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形又不是中心对称图形
6
B
【中考·上海】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.菱形
B.等边三角形
C.平行四边形
D.等腰梯形
7
A
2
知识点
中心对称图形的性质
中心对称图形性质:
过中心对称图形对称中心的直线将图形分成全
等的两部分.
合作探究
有一块如图所示的钢板,工人师傅想把它分成
面积相等的两部分,请你在图中画出分割方法.
例3
过中心对称图形对称中心的直线将图形分成全
等的两部分.可以将不规则图形分割成若干规
则的中心对称图形,然后再去解题.
导引:
钢板可看成由上、下两个长方形构成(如图所示),长
方形是中心对称图形,过对称中心的任一直线把长方
形分成全等的两部分,自然平分其面积,而长方形的
对称中心是两条对角线的交点,因此,先作出两长方
形的对称中心,过这两个对称中心作直线即可.(画法
不唯一)
解:
(1)利用过对称中心的任一直线将中心对称图形分割
成全等的两部分是平分面积的常用方法,而本题
的图形不是中心对称图形,我们则可以利用化整
为零的转化思想将其转化成两个中心对称图形,
再利用中心对称图形的性质来解决分割问题;
(2)本题还有其他分割方法,请分割试一试.
新知小结
如图,直线EF经过平行四边形ABCD的对角线
的交点O,若AE=2
cm,四边形AEFB的面积
为12
cm2,则CF=________,平行四边形
ABCD的面积为________.
1
2cm
24cm2
巩固新知
如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D分别关于点O中心对称;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的
个数为( )
A.2
B.3
C.4
D.5
2
D
【中考·宁波】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①②
B.②③
C.①③
D.①②③
3
A
3
知识点
中心对称图形的作图
如图,在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与阴影部分构成中心对称图形,该小正方形的序
号是__________.
例4
②
合作探究
先分别作出①②③④四种情况的图形,再运用中心
对称图形的定义加以识别.根据题意,可作出四种
情况的图形如图1,其中旋转180°后能与自身重合
的只有第2个图形,∴将②涂黑能构成中心对称图
形.如图2,故答案填②.
导引:
图1
图2
本题考查了中心对称图形的构造,
理解和应
用中心对称图形的定义是正确解答的关键.识别
中心对称图形的关键是看图形是否能绕某点旋转
180°后与原来图形重合.
新知小结
如图,长方形ABCD是篮球场的简图,请通过画图找出它的对称中心.
1
作图略,连接AC,BD,它们的交点就是对称中心.
解:
巩固新知
判断中心对称图形的“两个方法”:
(1)若一个图形上,存在这样的一个点,使整个图形
绕着这个点旋转180°后能够与原来的图形重合,
则这个图形就是中心对称图形.
(2)若图形中的对应点的连线都经过同一个点,并且
被这个点平分,则这个图形就是中心对称图形.
1
知识小结
归纳新知
有下列图形:①线段,②三角形,③平行四边形,④正方形,⑤圆,⑥等腰梯形.其中不是中心对称图形的是________(填序号).
易错点:对中心对称图形识别不清
2
易错小结
②⑥
①②③
错解的原因是对一些常见的图形不能正确分析.根据中心对称图形的概念,可知线段绕其中点旋转180°,平行四边形绕其对角线的交点旋转180°,正方形绕其对角线的交点旋转180°,圆绕其圆心旋转180°,都能与自身重合,都是中心对称图形,只有三角形和等腰梯形,找不到对称中心,故不是中心对称图形.
错解:
诊断:
重合
中心对称图形
对称中心
课后练习
D
C
全等
C
D
【答案】A
中点
交点
C
再见
第三章
图形的平移与旋转
3.1.2
中心对称图形
北师大版数学八年级下册
学习目标
1.了解中心对称图形的概念,以及两个图形成中心对称和中心对称图形的关系。
2.初步学会识别常见的中心对称图形或图案,并能用推理方式说明一个图形是中心对称图形。
我们上节课学习了中心对称的相关知识,中心对称是指两个图形的关系,而把这两个图形看作一个整体是什么图形呢?是我们这节课所要学习的中心对称图形.
导入新知
1
知识点
中心对称图形的定义
(1)如图,将线段AB绕它的中点旋转180°,你
有什么发现?
A
B
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
问
题
合作探究
(2)如图,将
ABCD
绕它的两条对角线的交点O旋
转180°,你有什么发现?
A
B
C
D
O
可以发现:
ABCD
绕它的两条对角线的交点O旋180°后与它本身重合.
像这样,把一个图形绕着某一个点旋转180°,
如果旋转后的图形能够与原来的图形重合,那么这
个图形叫做中心对称图形
这个点就是它的对称中心.
新知小结
中心对称与中心对称图形的区别与联系
:
中心对称
中心对称图形
区别
(1)是针对2个图形而言的
(2)是指两个图形的(位置)
关系
(3)对称点在两个图形上
(4)对称中心在两个图形之
间
(1)是针对1个图形而言的
(2)是指具有某种性质的一
个图形
(3)对称点在一个图形上
(4)对称中心在图形上或其
内部
联系
若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
例1
判断下列图形是否为中心对称图形.
解:(1)(3)(5)(6)(9)是中心对称图形,
(2)(4)(7)(8)不是中心对称图形.
(1)
(9)
(8)
(7)
(6)
(5)
(4)
(3)
(2)
合作探究
正多边形图案为中心对称图形的识别方法:边数为偶数的正多边形图案是中心对称图形,相应地,与边数为偶数的正多边形具有类似的特征的图形是中心对称图形;边数为奇数的正多边形或具有类似的特征的图形一定不是中心对称图形.
新知小结
如图,在下列图形中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
例2
导引:
这些图形绕某一点旋转一定角度都能与原图形完
全重合,但旋转180°后能与原图形重合的有3个,
只有最后一个图形不重合.
C
合作探究
正多边形图案是否为中心对称图形的识别方法:
边数为偶数的正多边形图案是中心对称图形,
相应地,与边数为偶数的正多边形具有类似的特
征的图形是中心对称图形;边数为奇数的正多边
形或具有类似的特征的图形一定不是中心对称图
形.
新知小结
下列哪些图形是中心对称图形?
1
解:中心对称图形有(1)(2)(3).
巩固新知
下面扑克牌中,哪些牌的牌面是中心对称图形?
2
解:第一张和第三张牌的牌面是中心对称图形.
【中考·玉林、崇左】五星红旗的每个五星( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
3
A
【中考·自贡】下列图形中,是轴对称图形,但不是中心对称图形的是( )
4
A
【中考·攀枝花】下列图形中,既是轴对称图形又是中心对称图形的是( )
5
D
如图,对其对称性描述正确的是( )
A.是轴对称图形
B.是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形又不是中心对称图形
6
B
【中考·上海】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.菱形
B.等边三角形
C.平行四边形
D.等腰梯形
7
A
2
知识点
中心对称图形的性质
中心对称图形性质:
过中心对称图形对称中心的直线将图形分成全
等的两部分.
合作探究
有一块如图所示的钢板,工人师傅想把它分成
面积相等的两部分,请你在图中画出分割方法.
例3
过中心对称图形对称中心的直线将图形分成全
等的两部分.可以将不规则图形分割成若干规
则的中心对称图形,然后再去解题.
导引:
钢板可看成由上、下两个长方形构成(如图所示),长
方形是中心对称图形,过对称中心的任一直线把长方
形分成全等的两部分,自然平分其面积,而长方形的
对称中心是两条对角线的交点,因此,先作出两长方
形的对称中心,过这两个对称中心作直线即可.(画法
不唯一)
解:
(1)利用过对称中心的任一直线将中心对称图形分割
成全等的两部分是平分面积的常用方法,而本题
的图形不是中心对称图形,我们则可以利用化整
为零的转化思想将其转化成两个中心对称图形,
再利用中心对称图形的性质来解决分割问题;
(2)本题还有其他分割方法,请分割试一试.
新知小结
如图,直线EF经过平行四边形ABCD的对角线
的交点O,若AE=2
cm,四边形AEFB的面积
为12
cm2,则CF=________,平行四边形
ABCD的面积为________.
1
2cm
24cm2
巩固新知
如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D分别关于点O中心对称;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的
个数为( )
A.2
B.3
C.4
D.5
2
D
【中考·宁波】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①②
B.②③
C.①③
D.①②③
3
A
3
知识点
中心对称图形的作图
如图,在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与阴影部分构成中心对称图形,该小正方形的序
号是__________.
例4
②
合作探究
先分别作出①②③④四种情况的图形,再运用中心
对称图形的定义加以识别.根据题意,可作出四种
情况的图形如图1,其中旋转180°后能与自身重合
的只有第2个图形,∴将②涂黑能构成中心对称图
形.如图2,故答案填②.
导引:
图1
图2
本题考查了中心对称图形的构造,
理解和应
用中心对称图形的定义是正确解答的关键.识别
中心对称图形的关键是看图形是否能绕某点旋转
180°后与原来图形重合.
新知小结
如图,长方形ABCD是篮球场的简图,请通过画图找出它的对称中心.
1
作图略,连接AC,BD,它们的交点就是对称中心.
解:
巩固新知
判断中心对称图形的“两个方法”:
(1)若一个图形上,存在这样的一个点,使整个图形
绕着这个点旋转180°后能够与原来的图形重合,
则这个图形就是中心对称图形.
(2)若图形中的对应点的连线都经过同一个点,并且
被这个点平分,则这个图形就是中心对称图形.
1
知识小结
归纳新知
有下列图形:①线段,②三角形,③平行四边形,④正方形,⑤圆,⑥等腰梯形.其中不是中心对称图形的是________(填序号).
易错点:对中心对称图形识别不清
2
易错小结
②⑥
①②③
错解的原因是对一些常见的图形不能正确分析.根据中心对称图形的概念,可知线段绕其中点旋转180°,平行四边形绕其对角线的交点旋转180°,正方形绕其对角线的交点旋转180°,圆绕其圆心旋转180°,都能与自身重合,都是中心对称图形,只有三角形和等腰梯形,找不到对称中心,故不是中心对称图形.
错解:
诊断:
重合
中心对称图形
对称中心
课后练习
D
C
全等
C
D
【答案】A
中点
交点
C
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
