2020-2021学年八年级数学北师大版下册 第三章 3.4 简单的图案设计 课件(共42张PPT)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第三章 3.4 简单的图案设计 课件(共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-11 20:23:46 | ||
图片预览








文档简介
(共42张PPT)
第三章
图形的平移与旋转
3.4
简单的图案设计
北师大版数学八年级下册
学习目标
1.利用旋转、轴对称或平移进行简单的图案设计。
2.认识和欣赏平移、旋转在现实生活中的应用,并灵活运用平移与旋转组合的方式进行一些图案设计。
问题:平移、轴对称变换、旋转有什么共同特征?
对称
左移
右移
导入新知
1
知识点
分析图案
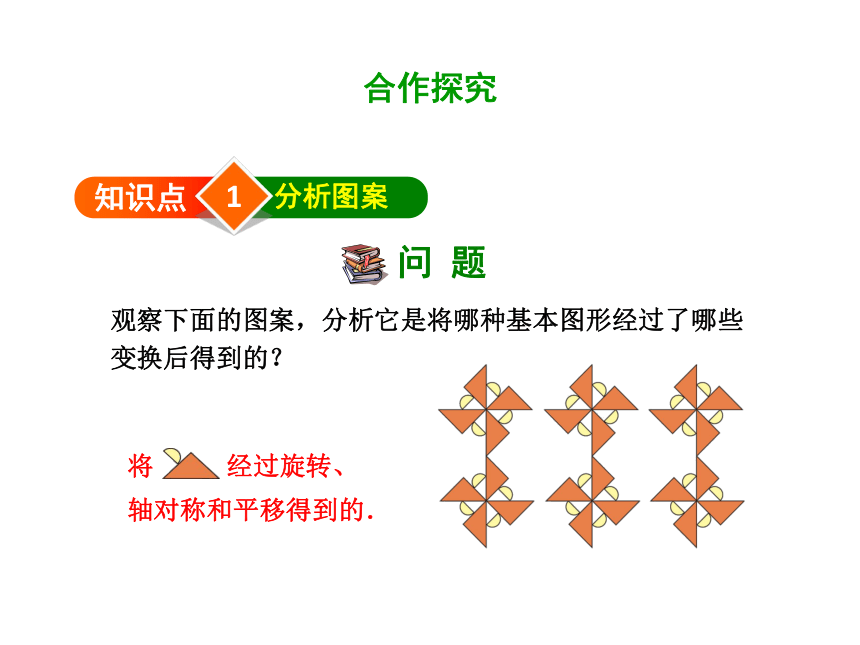
观察下面的图案,分析它是将哪种基本图形经过了哪些变换后得到的?
问
题
将
经过旋转、
轴对称和平移得到的.
合作探究
分析图案的形成过程应按如下步骤进行:
1.划分出组成原图案的最基本的图形;
2.说明将该基本图形运用平移、旋转、轴对称中
的哪些图形变换,通过怎样的变换方式得到原
图案.
1.平面图案的形成依据:平移,旋转和轴对称.
2.图形的变换不改变图形的形状和大小,只改变
图形的位置.
3.
常见的变换类型有:
(1)平移变换;
(2)旋转变换;
(3)轴对称变换;
(4)旋转变换与平移变换的组合;
(5)旋转变换与轴对称变换的组合;
(6)轴对称变换与平移变换的组合.
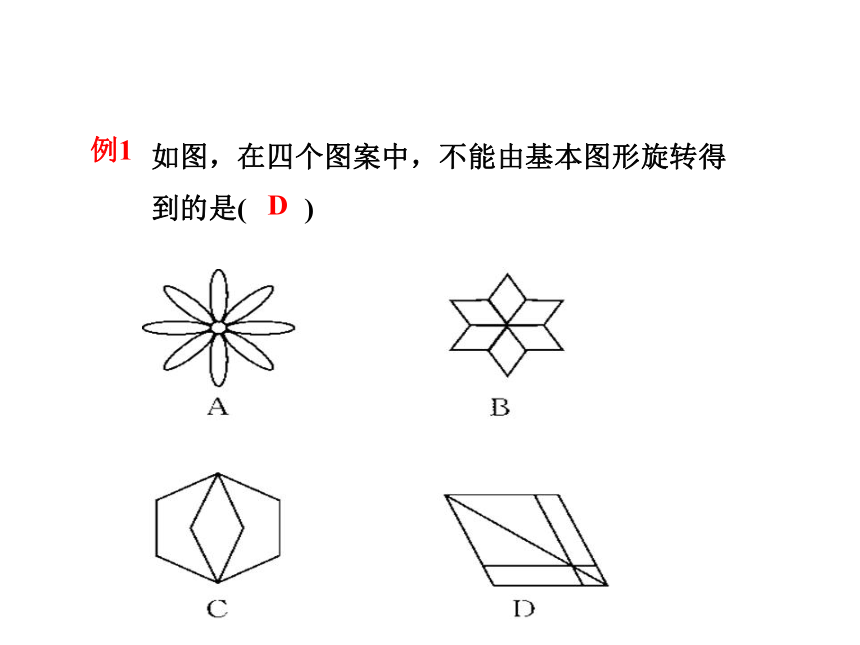
如图,在四个图案中,不能由基本图形旋转得到的是( )
例1
D
导引:
寻找基本图形、旋转中心、旋转角、旋转次数,
逐一判断.A.可由一个基本“花瓣”绕其中心
经过7次旋转,每次旋转45°得到;B.可由一个
基本“菱形”绕其中心经过5次旋转,每次旋转
60°得到;C.可由一个基本图形绕其中心旋转
180°得到;D.不能由基本图形旋转得到.
分析图案形成过程的一般步骤:
(1)确定设计图案的表达意图;
(2)分析图案所给定的基本图形;
(3)确定基本图形所进行的变换:平移变换、旋转
变换、对称变换.
新知小结
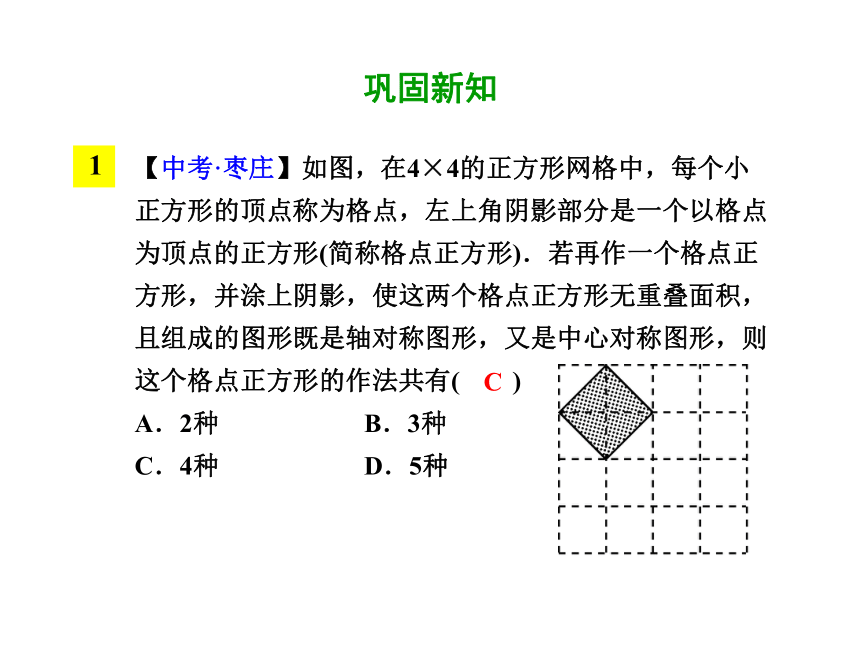
【中考·枣庄】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种
B.3种
C.4种
D.5种
1
C
巩固新知
2
知识点
设计图案
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
合作探究
学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△--(两个圆,两个等边三角形,两条线段)为构件,构思一个独特、有意义的轴对称图形,并写上一句简要的解说词.
例2
导引:
解答本例需要利用给定的六个元素,充分展开想
象的翅膀,组合成各种有意义的图形.此外,还
要有一定的生活经验和一定的文学修养.
所设计图形如图所示(答案不唯一,可供参考):
解:
本题考查了利用轴对称设计图案的知识,属于
开放型题,解答时注意三点:
①所作的图是轴对称图形,
②六个元素必须要用到,而且每个元素只用一次,
③解说词要和所设计的图形匹配,同学们要充分发
挥想象力及语言表达能力.
新知小结
把如图所示图形中左上角的图案绕着中心O旋
转90°,180°,270°,画出你所得的图案.
例3
合作探究
导引:
根据旋转图形的特征,分别把如上图
(1)(2)(3)所
示图形中左上角的图案绕着中心O旋转90°,
180°,270°,点O的位置不动,其余各部分均
绕点O按相同的方向旋转90°,180°,270°,
据此可画出各图.
画出的图案如图所示.
解:
本题是将基本图形按旋转图形的作法,分别
按三个角度作旋转图形.作旋转图形时注意旋转
三要素:旋转中心、旋转方向、旋转角.
新知小结
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
1
知识小结
归纳新知
如图所示的图案是由一个梯形经过旋转和对称形成的,则该梯形应该满足什么条件?
易错点:分析图案要从角和边两个角度去考虑
2
易错小结
因为该图案是由一个梯形作全等变换形成的,所以围绕一个顶点的三个角相等,所以该梯形的四个内角分别为120°,120°,60°
,60°.
该图案的设计不仅与梯形的角有关,而且与梯形的上下底和腰都有关.
该梯形的边应满足:上底等于腰且等于下底的一半;角应满足:四个内角分别为120°,120°,60°,60°.
错解:
正解:
诊断:
平移
旋转
轴对称
形状
大小
位置
课后练习
C
B
A
B
B
B
基本图形
轴对称
旋转
略.
C
A
③
再见
第三章
图形的平移与旋转
3.4
简单的图案设计
北师大版数学八年级下册
学习目标
1.利用旋转、轴对称或平移进行简单的图案设计。
2.认识和欣赏平移、旋转在现实生活中的应用,并灵活运用平移与旋转组合的方式进行一些图案设计。
问题:平移、轴对称变换、旋转有什么共同特征?
对称
左移
右移
导入新知
1
知识点
分析图案
观察下面的图案,分析它是将哪种基本图形经过了哪些变换后得到的?
问
题
将
经过旋转、
轴对称和平移得到的.
合作探究
分析图案的形成过程应按如下步骤进行:
1.划分出组成原图案的最基本的图形;
2.说明将该基本图形运用平移、旋转、轴对称中
的哪些图形变换,通过怎样的变换方式得到原
图案.
1.平面图案的形成依据:平移,旋转和轴对称.
2.图形的变换不改变图形的形状和大小,只改变
图形的位置.
3.
常见的变换类型有:
(1)平移变换;
(2)旋转变换;
(3)轴对称变换;
(4)旋转变换与平移变换的组合;
(5)旋转变换与轴对称变换的组合;
(6)轴对称变换与平移变换的组合.
如图,在四个图案中,不能由基本图形旋转得到的是( )
例1
D
导引:
寻找基本图形、旋转中心、旋转角、旋转次数,
逐一判断.A.可由一个基本“花瓣”绕其中心
经过7次旋转,每次旋转45°得到;B.可由一个
基本“菱形”绕其中心经过5次旋转,每次旋转
60°得到;C.可由一个基本图形绕其中心旋转
180°得到;D.不能由基本图形旋转得到.
分析图案形成过程的一般步骤:
(1)确定设计图案的表达意图;
(2)分析图案所给定的基本图形;
(3)确定基本图形所进行的变换:平移变换、旋转
变换、对称变换.
新知小结
【中考·枣庄】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种
B.3种
C.4种
D.5种
1
C
巩固新知
2
知识点
设计图案
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
合作探究
学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△--(两个圆,两个等边三角形,两条线段)为构件,构思一个独特、有意义的轴对称图形,并写上一句简要的解说词.
例2
导引:
解答本例需要利用给定的六个元素,充分展开想
象的翅膀,组合成各种有意义的图形.此外,还
要有一定的生活经验和一定的文学修养.
所设计图形如图所示(答案不唯一,可供参考):
解:
本题考查了利用轴对称设计图案的知识,属于
开放型题,解答时注意三点:
①所作的图是轴对称图形,
②六个元素必须要用到,而且每个元素只用一次,
③解说词要和所设计的图形匹配,同学们要充分发
挥想象力及语言表达能力.
新知小结
把如图所示图形中左上角的图案绕着中心O旋
转90°,180°,270°,画出你所得的图案.
例3
合作探究
导引:
根据旋转图形的特征,分别把如上图
(1)(2)(3)所
示图形中左上角的图案绕着中心O旋转90°,
180°,270°,点O的位置不动,其余各部分均
绕点O按相同的方向旋转90°,180°,270°,
据此可画出各图.
画出的图案如图所示.
解:
本题是将基本图形按旋转图形的作法,分别
按三个角度作旋转图形.作旋转图形时注意旋转
三要素:旋转中心、旋转方向、旋转角.
新知小结
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
1
知识小结
归纳新知
如图所示的图案是由一个梯形经过旋转和对称形成的,则该梯形应该满足什么条件?
易错点:分析图案要从角和边两个角度去考虑
2
易错小结
因为该图案是由一个梯形作全等变换形成的,所以围绕一个顶点的三个角相等,所以该梯形的四个内角分别为120°,120°,60°
,60°.
该图案的设计不仅与梯形的角有关,而且与梯形的上下底和腰都有关.
该梯形的边应满足:上底等于腰且等于下底的一半;角应满足:四个内角分别为120°,120°,60°,60°.
错解:
正解:
诊断:
平移
旋转
轴对称
形状
大小
位置
课后练习
C
B
A
B
B
B
基本图形
轴对称
旋转
略.
C
A
③
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
