2020-2021学年八年级数学苏科版下册第九章中心对称-平行四边形单元复习测试题一(word版无答案)
文档属性
| 名称 | 2020-2021学年八年级数学苏科版下册第九章中心对称-平行四边形单元复习测试题一(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 189.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览


文档简介
第九章中心对称-平行四边形期中复习测试题一
一、选择题
1.下列各图中,既是轴对称图形又是中心对称图形的是( )
A
B
C
D
2.下列说法不正确的是(??
)
A.有两组对边分别平行的四边形是平行四边形
B.平行四边形的对角线互相平分
C.平行四边形的对角互补
D.平行四边形的对边平行且相等
3.菱形、矩形都具有的性质(
)
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.四个角是直角
4.如图,菱形ABCD
中,对角线AC
、BD
交于点O
,
E为边AD
中点,菱形ABCD
的周长为28,则
OE的长等于(
)
A.14
B.7
C.4
D.3.5
5.如图,平行四边形ABCD的周长是32cm,△ABC的周长是26cm,E、F分别是边AB、BC的中点,则EF的长为( )
A.8cm
B.6cm
C.5cm
D.4cm
6.如图,P是正方形ABCD内一点,连结PA、PB、PC、PD,若△PAB是等边三角形,则∠DPA的度数是( )
A.60°
B.75°
C.80°
D.90°
7.如图,四边形OABC是平行四边形,O是坐标原点,A,C坐标分别是(1,2),(3,0),则B点坐标是( )
A.(4,2)
B.(4,3)
C.(3,2)
D.无法确定
如图,正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=
3,则的AF+CE为( )
A.2
B.6
C.8
D.10
二、填空题
9.如图,将绕点按逆时针方向旋转后得到,若,则的度数是__________.
10.如图,在?ABCD中,∠A=55°,则∠D=____°.
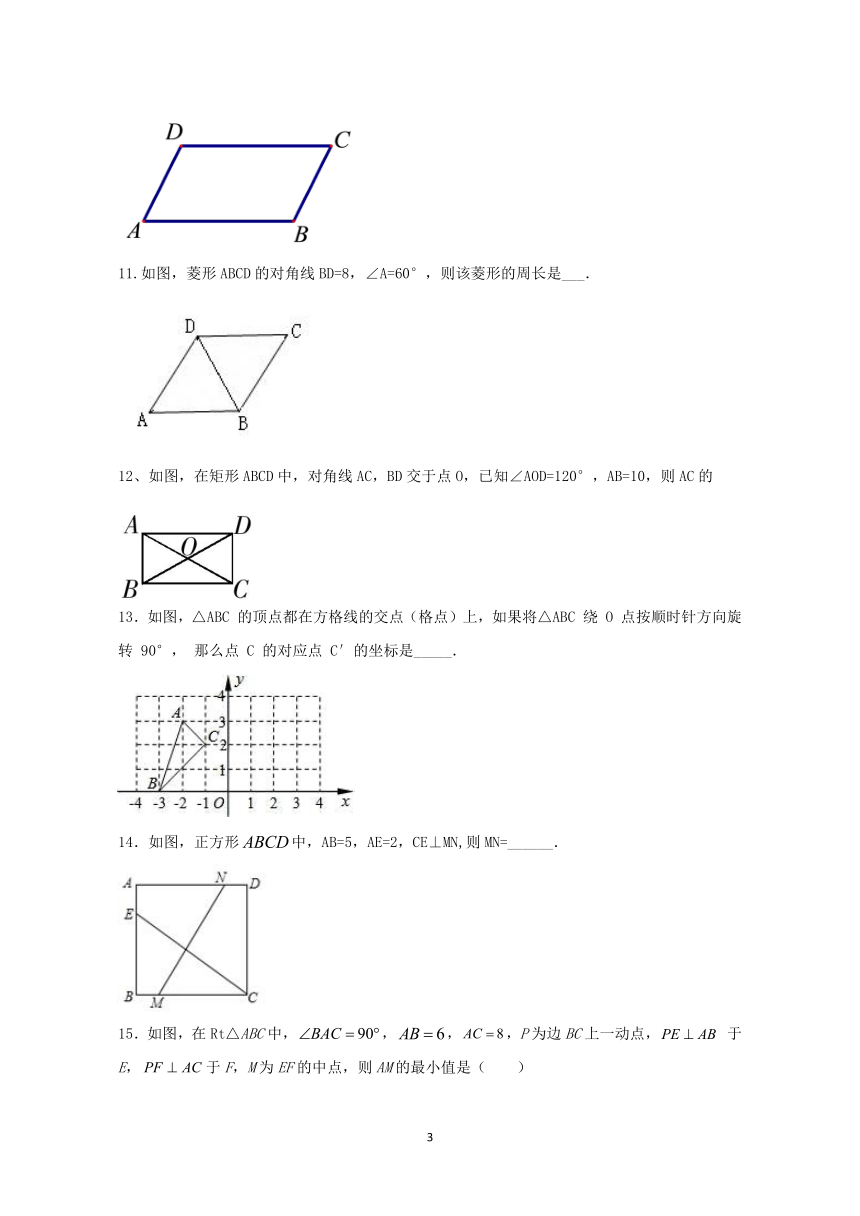
11.如图,菱形ABCD的对角线BD=8,∠A=60°,则该菱形的周长是___.
12、如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=10,则AC的
13.如图,△ABC
的顶点都在方格线的交点(格点)上,如果将△ABC
绕
O
点按顺时针方向旋转
90°,
那么点
C
的对应点
C′的坐标是_____.
14.如图,正方形中,AB=5,AE=2,CE⊥MN,则MN=______.
15.如图,在Rt△ABC中,,,,P为边BC上一动点,
于E,于F,M为EF的中点,则AM的最小值是(
)
A.2.5
B.2.4
C.2
D.3
16.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是__________.
三、简答题
17.已知平行四边形ABCD中,DE=BF
(1)求证:四边形AFCE是平行四边形
(2)如图,当∠1=
°时,AC=EF.
18.已知:矩形的对角线ABCD的对角线AC、BD相交于点O,E、F、G、H分别在AO、BO、CO、DO上,且AH=BF=CG=DE
求证:四边形EFGH是矩形
19.已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,
CF∥BD,DF//AC。求证:]四边形ODFC是菱形:]
20、已知:如图,在△ABC中,∠ACB=90°,D是AB的中点,E是BC的中点,
DF分别是△ADC的角平分线.求证:四边形DECF是矩形.
21.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
22.如图,矩形
ABCD
中,AB=5,BC=3,点
E
为
CD
边上一点.
(1)当
AE
平分∠BED
时,求
DE
的长.
(2)你能把矩形
ABCD
沿某条直线剪一刀分成两块,再拼成一个菱形吗?如果能,在备用图中画出示意图,并计算菱形较长对角线的长.
23定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD.
(1)请结合图形,写出筝形两种不同类型的性质:性质1:
;性质2:
.
(2)若AB∥CD,求证:四边形ABCD为菱形.
24.
平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
一、选择题
1.下列各图中,既是轴对称图形又是中心对称图形的是( )
A
B
C
D
2.下列说法不正确的是(??
)
A.有两组对边分别平行的四边形是平行四边形
B.平行四边形的对角线互相平分
C.平行四边形的对角互补
D.平行四边形的对边平行且相等
3.菱形、矩形都具有的性质(
)
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.四个角是直角
4.如图,菱形ABCD
中,对角线AC
、BD
交于点O
,
E为边AD
中点,菱形ABCD
的周长为28,则
OE的长等于(
)
A.14
B.7
C.4
D.3.5
5.如图,平行四边形ABCD的周长是32cm,△ABC的周长是26cm,E、F分别是边AB、BC的中点,则EF的长为( )
A.8cm
B.6cm
C.5cm
D.4cm
6.如图,P是正方形ABCD内一点,连结PA、PB、PC、PD,若△PAB是等边三角形,则∠DPA的度数是( )
A.60°
B.75°
C.80°
D.90°
7.如图,四边形OABC是平行四边形,O是坐标原点,A,C坐标分别是(1,2),(3,0),则B点坐标是( )
A.(4,2)
B.(4,3)
C.(3,2)
D.无法确定
如图,正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=
3,则的AF+CE为( )
A.2
B.6
C.8
D.10
二、填空题
9.如图,将绕点按逆时针方向旋转后得到,若,则的度数是__________.
10.如图,在?ABCD中,∠A=55°,则∠D=____°.
11.如图,菱形ABCD的对角线BD=8,∠A=60°,则该菱形的周长是___.
12、如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=10,则AC的
13.如图,△ABC
的顶点都在方格线的交点(格点)上,如果将△ABC
绕
O
点按顺时针方向旋转
90°,
那么点
C
的对应点
C′的坐标是_____.
14.如图,正方形中,AB=5,AE=2,CE⊥MN,则MN=______.
15.如图,在Rt△ABC中,,,,P为边BC上一动点,
于E,于F,M为EF的中点,则AM的最小值是(
)
A.2.5
B.2.4
C.2
D.3
16.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是__________.
三、简答题
17.已知平行四边形ABCD中,DE=BF
(1)求证:四边形AFCE是平行四边形
(2)如图,当∠1=
°时,AC=EF.
18.已知:矩形的对角线ABCD的对角线AC、BD相交于点O,E、F、G、H分别在AO、BO、CO、DO上,且AH=BF=CG=DE
求证:四边形EFGH是矩形
19.已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,
CF∥BD,DF//AC。求证:]四边形ODFC是菱形:]
20、已知:如图,在△ABC中,∠ACB=90°,D是AB的中点,E是BC的中点,
DF分别是△ADC的角平分线.求证:四边形DECF是矩形.
21.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
22.如图,矩形
ABCD
中,AB=5,BC=3,点
E
为
CD
边上一点.
(1)当
AE
平分∠BED
时,求
DE
的长.
(2)你能把矩形
ABCD
沿某条直线剪一刀分成两块,再拼成一个菱形吗?如果能,在备用图中画出示意图,并计算菱形较长对角线的长.
23定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD.
(1)请结合图形,写出筝形两种不同类型的性质:性质1:
;性质2:
.
(2)若AB∥CD,求证:四边形ABCD为菱形.
24.
平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
