数学八年级上人教新课标11.3角平分线的性质第2课时课件
文档属性
| 名称 | 数学八年级上人教新课标11.3角平分线的性质第2课时课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 363.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-17 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
人教版八年级数学(上)
11.3角的平分线的性质(2)
A
D
B
C
E
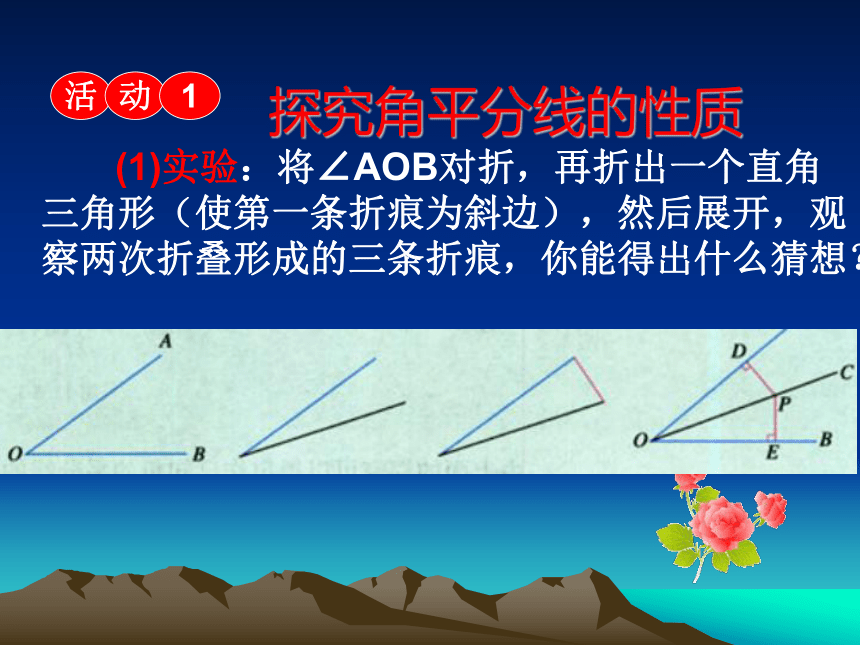
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么猜想?
活
动
1
探究角平分线的性质
(2)猜想:角的平分线上的点到角的两边的距离相等.
活
动
2
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
探究角平分线的性质
活
动
3
(3)证明猜想
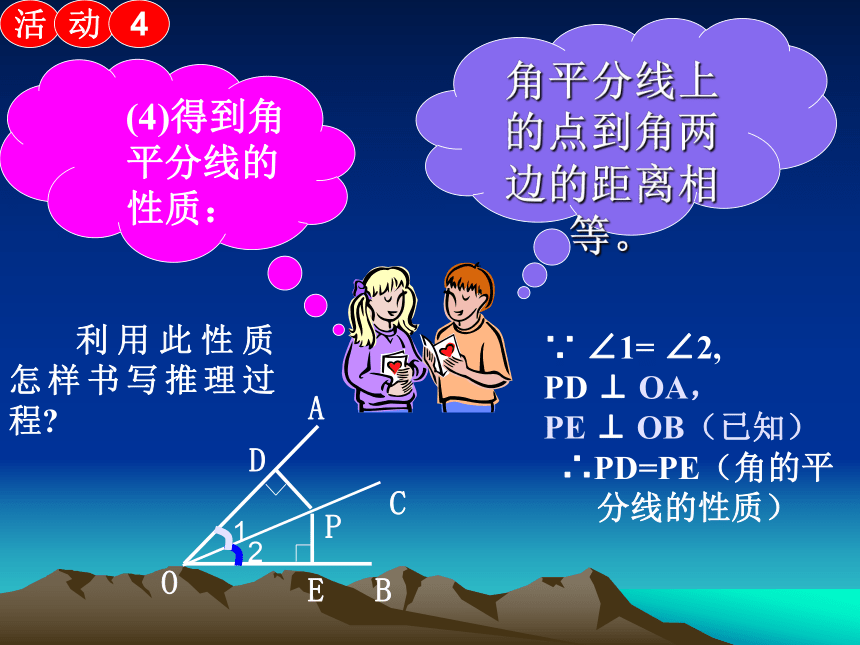
角平分线上的点到角两边的距离相等。
(4)得到角平分线的性质:
活
动
4
利用此性质怎样书写推理过程
∵ ∠1= ∠2,
PD ⊥ OA, PE ⊥ OB(已知)
∴PD=PE(角的平分线的性质)
P
A
O
B
C
E
D
1
2
活
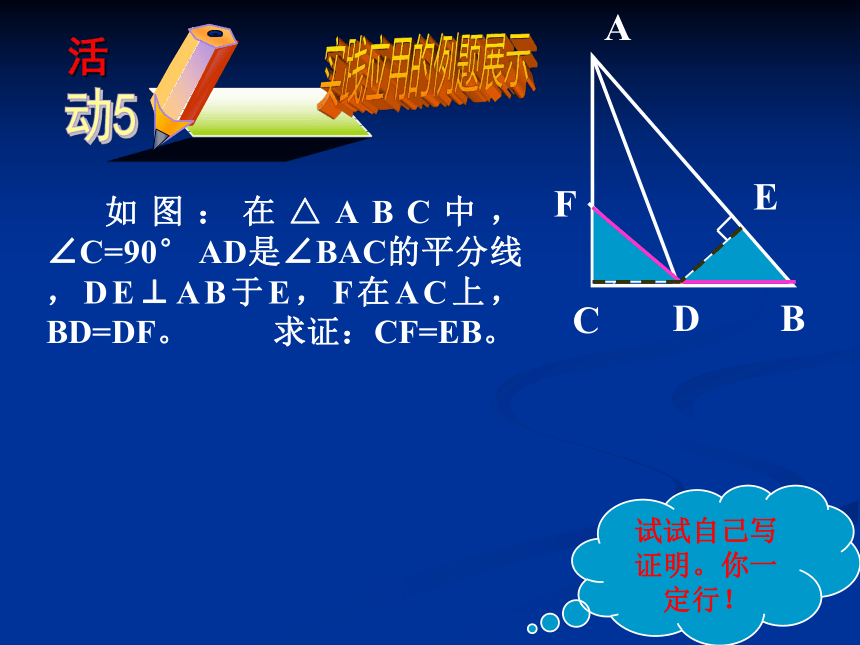
如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF。 求证:CF=EB。
A
C
D
E
B
F
试试自己写证明。你一定行!
证明:∵ ∠C=90°,
∴DC⊥AC于C点。
又∵DE⊥AB于E点,AD平分∠BAC,
∴DE=DC。
在Rt△DBE和Rt△DFC中
DB=DF,
DE=DC.
∴Rt△DBE≌ Rt△DFC(HL)。
∴CF=EB(全等三角形的性质)。
活
{
A
C
D
E
B
F
一填空题:
1、如图,∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)。
A
C
D
E
B
1
2
DC=DE
角平分线上的点到角的两边的距离相 等
随
练习1
2、如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,若CD=6,则点D到AB的距离为__。
6
A
C
B
D
二、判断题:
1、∵ 如图,AD平分∠BAC(已知)
∴ BD = DC ,
( )
角的平分线上的点到角的两边的距离相等。
2、在右图中如果再加上 ∠1+∠3=∠2+∠4=90°,
∴ BD = DC。
随
练习2
1
2
3
4
三、证明题:
△ABC中,AD是它的角平分线,且BD= CD,DE⊥AB,DF⊥AC,垂足分别为E,F。
求证:EB=FC。
随
练习3
E
A
D
B
C
F
证明:∵ AD平分∠BAC, DE⊥AB, DF⊥AC,
∴ DE=DF.
在Rt△DBE和Rt△DCF中
DE=DF,DB=DC
∴ Rt△DBE≌Rt△DCF(HL)。
∴ EB=FC。
小结: 在这一节课上我们学习了角的平分线的性质的探究与应用,其中角的平分线的性质的探究又分为实验、猜想、证明猜想、得到性质四个部分进行。
作业:
习题11.3(2、3)。.
再 见
人教版八年级数学(上)
11.3角的平分线的性质(2)
A
D
B
C
E
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么猜想?
活
动
1
探究角平分线的性质
(2)猜想:角的平分线上的点到角的两边的距离相等.
活
动
2
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
探究角平分线的性质
活
动
3
(3)证明猜想
角平分线上的点到角两边的距离相等。
(4)得到角平分线的性质:
活
动
4
利用此性质怎样书写推理过程
∵ ∠1= ∠2,
PD ⊥ OA, PE ⊥ OB(已知)
∴PD=PE(角的平分线的性质)
P
A
O
B
C
E
D
1
2
活
如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF。 求证:CF=EB。
A
C
D
E
B
F
试试自己写证明。你一定行!
证明:∵ ∠C=90°,
∴DC⊥AC于C点。
又∵DE⊥AB于E点,AD平分∠BAC,
∴DE=DC。
在Rt△DBE和Rt△DFC中
DB=DF,
DE=DC.
∴Rt△DBE≌ Rt△DFC(HL)。
∴CF=EB(全等三角形的性质)。
活
{
A
C
D
E
B
F
一填空题:
1、如图,∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)。
A
C
D
E
B
1
2
DC=DE
角平分线上的点到角的两边的距离相 等
随
练习1
2、如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,若CD=6,则点D到AB的距离为__。
6
A
C
B
D
二、判断题:
1、∵ 如图,AD平分∠BAC(已知)
∴ BD = DC ,
( )
角的平分线上的点到角的两边的距离相等。
2、在右图中如果再加上 ∠1+∠3=∠2+∠4=90°,
∴ BD = DC。
随
练习2
1
2
3
4
三、证明题:
△ABC中,AD是它的角平分线,且BD= CD,DE⊥AB,DF⊥AC,垂足分别为E,F。
求证:EB=FC。
随
练习3
E
A
D
B
C
F
证明:∵ AD平分∠BAC, DE⊥AB, DF⊥AC,
∴ DE=DF.
在Rt△DBE和Rt△DCF中
DE=DF,DB=DC
∴ Rt△DBE≌Rt△DCF(HL)。
∴ EB=FC。
小结: 在这一节课上我们学习了角的平分线的性质的探究与应用,其中角的平分线的性质的探究又分为实验、猜想、证明猜想、得到性质四个部分进行。
作业:
习题11.3(2、3)。.
再 见
