2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》单元综合培优训练(word版含解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》单元综合培优训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 106.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 20:07:02 | ||
图片预览



文档简介
2021年苏科版七年级数学下册《第9章整式乘法与因式分解》单元综合培优训练(附答案)
1.已知a,b,c是△ABC的三条边长,且(a+b+c)(a﹣b)=0,则△ABC一定是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.以上均不对
2.要使(x2﹣x+5)(2x2﹣ax﹣4)展开式中不含x2项,则a的值等于( )
A.﹣6
B.6
C.14
D.﹣14
3.已知x2+x=1,那么x4+2x3﹣x2﹣2x+2020的值为( )
A.2019
B.2020
C.2021
D.2022
4.下列各式:①﹣x2﹣y2;②﹣a2b2+1;
③a2+ab+b2;
④﹣x2+2xy﹣y2;⑤﹣mn+m2n2,用公式法分解因式的有( )
A.2个
B.3个
C.4个
D.5个
5.若a2﹣b2=16,(a+b)2=8,则ab的值为( )
A.﹣
B.
C.﹣6
D.6
6.已知a﹣b=b﹣c=2,a2+b2+c2=11,则ab+bc+ac=( )
A.﹣22
B.﹣1
C.7
D.11
7.已知664﹣1能被30﹣40之间的两个整数整除,则这两个整数是( )
A.35,37
B.35,36
C.34,38
D.36,37
8.下列各项分解因式正确的是( )
A.a2﹣1=(a﹣1)2
B.a2﹣4a+2=(a﹣2)2
C.﹣b2+a2=(a+b)(a﹣b)
D.x2﹣2x﹣3=(x﹣1)(x+3)
9.若x2+5x+m=(x+n)2,则m,n的值分别为( )
A.m=,n=
B.m=,n=5
C.m=25,n=5
D.m=5,n=
10.已知x2﹣2(m+1)xy+16y2是一个完全平方式,则(m2﹣5m﹣14)÷(m+2)=
.
11.若(x+2)(x+a)=x2+bx﹣8,则ab的值为
.
12.如图.现有正方形卡片A类,B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b),宽为(3a+2b)的大长方形,那么需要C类卡片的张数是
.
13.若a﹣b=﹣2,则a2﹣ab+2b=
.
14.如图,边长分别为a,b的两个正方形并排放在一起,当a+b=16,ab=60时阴影部分的面积为
.
15.若x2﹣2x﹣6=0,则(x﹣3)2+(2x+1)(2x﹣1)﹣2x2的值为
.
16.已知4x=10,25y=10,则(x﹣2)(y﹣2)+3(xy﹣1)的值为
.
17.已知a﹣b=5,ab=﹣2,则代数式a2+b2﹣2021的值是
.
18.因式分解:15x2+13xy﹣44y2=
.
19.已知ax2+bx+1与2x2﹣3x+1的积不含x3项,也不含x项,求a与b的值.
20.为探求1×2+2×3+3×4+…+n(n+1)的值,喜欢研究的小明同学发现有下面三个等式:
1×2=(1×2×3﹣0×1×2)
2×3=(2×3×4﹣1×2×3)
3×4=(3×4×5﹣2×3×4)
他将这三个式子相加得到1×2+2×3+3×4=×3×4×5.
请你沿着小明的思路继续研究:
(1)填空:计算1×2+2×3+3×4+…+100×101=
.
计算1×2+2×3+3×4+…+n×(n+1)=
.
(2)利用(1)的规律计算:2×4+4×6+6×8+…+100×102.
(3)继续研究,计算1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)的公式(要求仿照小明的思路写出推导过程).
21.阅读理解:
若x满足(30﹣x)(x﹣10)=160,求(30﹣x)2+(x﹣10)2的值.
解:设30﹣x=a,x﹣10=b,则(30﹣x)(x﹣10)=ab=160,a+b=(30﹣x)+(x﹣10)=20,(30﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=202﹣2×160=80
解决问题:
(1)若x满足(2020﹣x)(x﹣2016)=2.则(2020﹣x)2+(x﹣2016)2=
;
(2)若x满足(2021﹣x)2+(x﹣2018)2=2020,求(2021﹣x)(x﹣2018)的值;
(3)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为
平方单位.
22.计算:
(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2.
23.先化简,再求值:x(x+y)﹣(2x﹣3y)(x﹣y)+(x﹣2y)(x+2y),
其中x=3,y=﹣1.
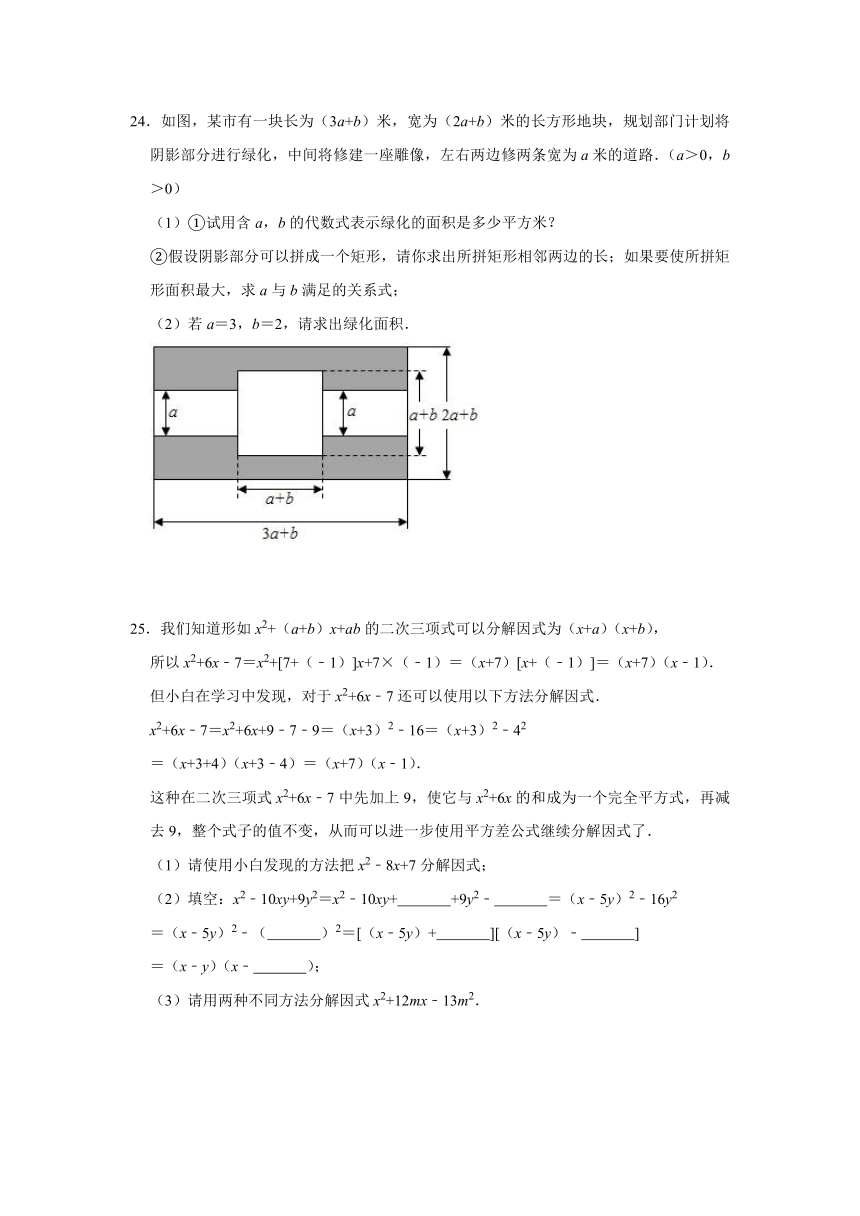
24.如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.(a>0,b>0)
(1)①试用含a,b的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形,请你求出所拼矩形相邻两边的长;如果要使所拼矩形面积最大,求a与b满足的关系式;
(2)若a=3,b=2,请求出绿化面积.
25.我们知道形如x2+(a+b)x+ab的二次三项式可以分解因式为(x+a)(x+b),
所以x2+6x﹣7=x2+[7+(﹣1)]x+7×(﹣1)=(x+7)[x+(﹣1)]=(x+7)(x﹣1).
但小白在学习中发现,对于x2+6x﹣7还可以使用以下方法分解因式.
x2+6x﹣7=x2+6x+9﹣7﹣9=(x+3)2﹣16=(x+3)2﹣42
=(x+3+4)(x+3﹣4)=(x+7)(x﹣1).
这种在二次三项式x2+6x﹣7中先加上9,使它与x2+6x的和成为一个完全平方式,再减去9,整个式子的值不变,从而可以进一步使用平方差公式继续分解因式了.
(1)请使用小白发现的方法把x2﹣8x+7分解因式;
(2)填空:x2﹣10xy+9y2=x2﹣10xy+
+9y2﹣
=(x﹣5y)2﹣16y2
=(x﹣5y)2﹣(
)2=[(x﹣5y)+
][(x﹣5y)﹣
]
=(x﹣y)(x﹣
);
(3)请用两种不同方法分解因式x2+12mx﹣13m2.
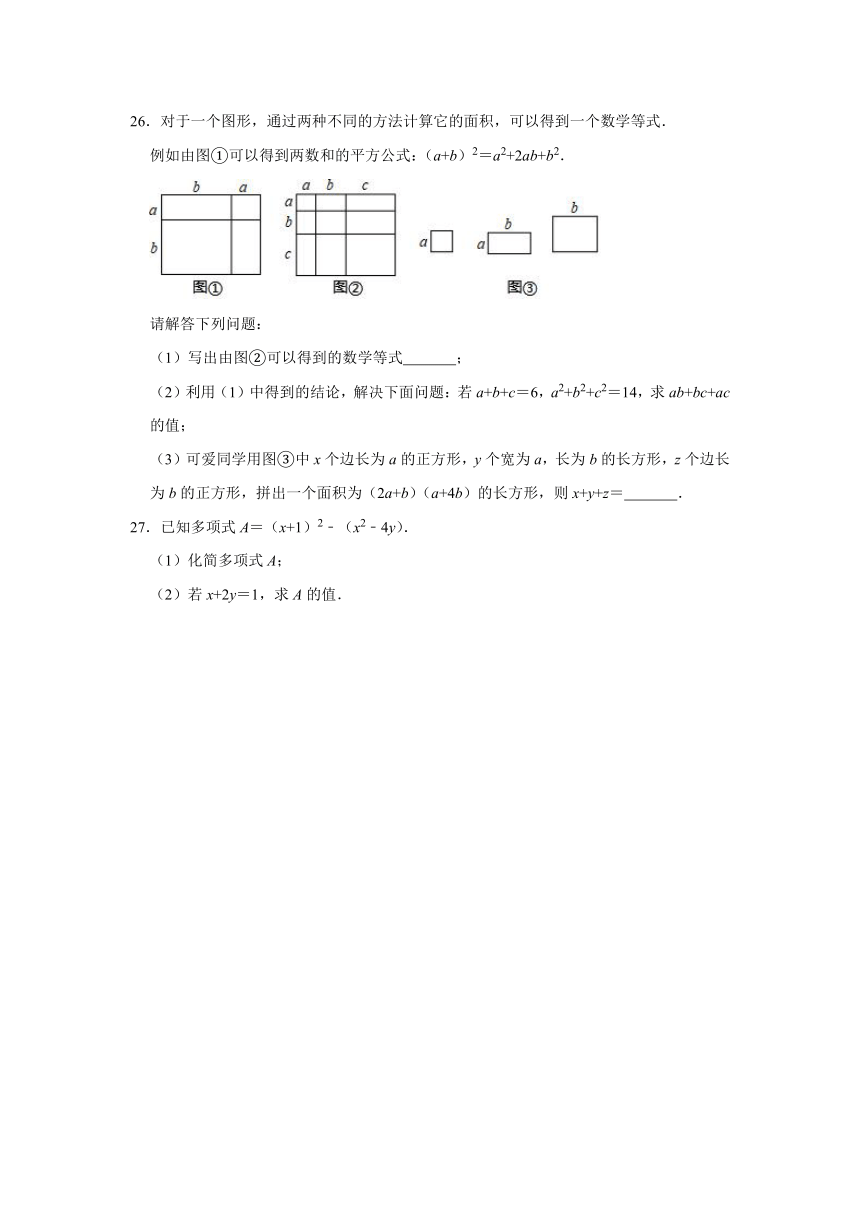
26.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.
例如由图①可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.
请解答下列问题:
(1)写出由图②可以得到的数学等式
;
(2)利用(1)中得到的结论,解决下面问题:若a+b+c=6,a2+b2+c2=14,求ab+bc+ac的值;
(3)可爱同学用图③中x个边长为a的正方形,y个宽为a,长为b的长方形,z个边长为b的正方形,拼出一个面积为(2a+b)(a+4b)的长方形,则x+y+z=
.
27.已知多项式A=(x+1)2﹣(x2﹣4y).
(1)化简多项式A;
(2)若x+2y=1,求A的值.
参考答案
1.解:∵(a+b+c)(a﹣b)=0,
∴a+b+c=0或a﹣b=0,
∵a,b,c是△ABC的三条边长,
∴a+b+c>0,
∴a﹣b=0,即a=b,
∴△ABC一定是等腰三角形.
故选:A.
2.解:(x2﹣x+5)(2x2﹣ax﹣4)
=2x4﹣ax3﹣4x2﹣2x3+ax2+4x+10x2﹣5ax﹣20
=2x4﹣(a+2)x3+(a+6)x2+(4﹣5a)x﹣20,
∵展开式中不含x2项,
∴a+6=0,
∴a=﹣6,
故选:A.
3.解:∵x2+x=1,
∴x4+2x3﹣x2﹣2x+2020=x4+x3+x3﹣x2﹣2x+2020
=x2(x2+x)+x3﹣x2﹣2x+2020=x2+x3﹣x2﹣2x+2020
=x(x2+x)﹣x2﹣2x+2020=x﹣x2﹣2x+2020
=﹣x2﹣x+2020=﹣(x2+x)+2020=﹣1+2020=2019.故选:A.
4.解:①﹣x2﹣y2=﹣(x2+y2),因此①不能用公式法分解因式;
②﹣a2b2+1=1﹣(ab)2=(1+ab)(1﹣ab),因此②能用公式法分解因式;
③a2+ab+b2不符合完全平方公式的结果特征,因此③不能用公式法分解因式;
④﹣x2+2xy﹣y2=﹣(x2﹣2xy+y2)=﹣(x﹣y)2,因此④能用公式法分解因式;
⑤﹣mn+m2n2=(﹣mn)2,因此⑤能用公式法分解因式;
综上所述,能用公式法分解因式的有②④⑤,
故选:B.
5.解:∵a2﹣b2=16,
∴(a+b)(a﹣b)=16,
∴(a+b)2(a﹣b)2=256,
∵(a+b)2=8,
∴(a﹣b)2=32,
∴ab===﹣6,
故选:C.
6.解:∵a﹣b=b﹣c=2,
∴a﹣c=4,
∴a2+b2+c2﹣ab﹣bc﹣ac=(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)=[(a﹣b)2+(b﹣c)2+(c﹣a)2]=12,
∴ab+bc+ac=a2+b2+c2﹣12=﹣1,
故选:B.
7.解:664﹣1=(632+1)(632﹣1)=(632+1)(616+1)(616﹣1)
=(632+1)(616+1)(68+1)(68﹣1)=(632+1)(616+1)(68+1)(64+1)(64﹣1)
=(632+1)(616+1)(68+1)(64+1)(62+1)(62﹣1)
=(632+1)(616+1)(68+1)(64+1)×37×35.
故选:A.
8.解:A、a2﹣1=(a+1)(a﹣1),所以A选项错误;
B、a2﹣4a+2在实数范围内不能因式分解;
C、﹣b2+a2=a2﹣b2=(a+b)(a﹣b),所以C选项正确;
D、x2﹣2x﹣3=(x﹣3)(x+1),所以D选项错误.
故选:C.
9.解:∵x2+5x+m=(x+n)2=x2+2nx+n2,
∴2n=5,m=n2,
解得m=,n=,
故选:A.
10.解:∵x2﹣2(m+1)xy+16y2是一个完全平方式,
∴﹣2(m+1)xy=±2?x?4y,
解得:m=3或﹣5,
(m2﹣5m﹣14)÷(m+2)=(m+2)(m﹣7)÷(m+2)=m﹣7,
当m=3时,原式=3﹣7=﹣4;
当m=﹣5时,原式=﹣5﹣7=﹣12;
故答案为:﹣4或﹣12.
11.解:∵(x+2)(x+a)=x2+(2+a)x+2a,
又∵(x+2)(x+a)=x2+bx﹣8,
∴x2+(2+a)x+2a=x2+bx﹣8.
∴2+a=b,2a=﹣8.
∴a=﹣4,b=﹣2.
∴ab=(﹣4)﹣2==.故答案为:.
12.解:∵(a+3b)(3a+2b)=3a2+11ab+6b2,
∵一张C类卡片的面积为ab,
∴需要C类卡片11张.
故答案为:11.
13.解:∵a﹣b=﹣2,
∴a2﹣ab+2b=a(a﹣b)+2b=﹣2a+2b=﹣2(a﹣b)=4.
故答案为:4.
14.解:根据题意得:S阴影部分=a2+b2﹣a2﹣b(a+b)=a2+b2﹣a2﹣ab﹣b2
=(a2+b2﹣ab)=[(a+b)2﹣3ab],
把a+b=16,ab=60代入得:S阴影部分=38.
故图中阴影部分的面积为38.
故答案为38.
15.解:∵x2﹣2x﹣6=0,
∴x2﹣2x=6,
∴(x﹣3)2+(2x+1)(2x﹣1)﹣2x2=x2﹣6x+9+4x2﹣1﹣2x2=3x2﹣6x+8
=3(x2﹣2x)+8=3×6+8=26,
故答案为:26.
16.解:∵,
∴由①得4xy=10y,③
由②得25xy=10x,④
∴③×④得4xy?25xy=10y?10x,即(4×25)xy=10x+y,
∴(102)xy=10x+y,
∴102xy=10x+y,
∴2xy=x+y
(x﹣2)(y﹣2)+3(xy﹣1)=xy﹣2x﹣2y+4+3xy﹣3=4xy﹣2(x+y)+1
=4xy﹣2×2xy+1=1.故答案为:1.
17.解:a2+b2﹣2021=(a﹣b)2+2ab﹣2021=52﹣4﹣2021=-2001.故答案为:-2001
18.解:利用十字相乘法,如图,
将二次项系数、常数项分别分解,交叉乘加验中项,得出答案,
15x2+13xy﹣44y2=(3x﹣4y)(5x+11y).
故答案为:(3x﹣4y)(5x+11y).
19.解:根据题意列得:(ax2+bx+1)(2x2﹣3x+1)=2ax4+(2b﹣3a)x3+(a+2﹣3b)x2+(b﹣3)x+1,
∵不含x3的项,也不含x的项,
∴2b﹣3a=0,b﹣3=0,
解得a=2,b=3.
20.解:(1)1×2+2×3+3×4+…+100×101=(100×101×102)=343400,
1×2+2×3+3×4+…+n×(n+1)=n×(n+1)(n+2),
故答案为:343400,n(n+1)(n+2);
(2)仿照上述的方法可得,
2×4=(2×4×6﹣0×2×4),
4×6=(4×6×8﹣2×4×6),
6×8=(6×8×10﹣4×6×8),
……
100×102=(100×102×104﹣98×100×102),
将上式相加得,
2×4+4×6+6×8+…+100×102=(100×102×104)=176800;
(3)仿照上述的方法可得,
1×2×3=(1×2×3×4﹣0×1×2×3),
2×3×4=(2×3×4×5﹣1×2×3×4),
3×4×5=(3×4×5×6﹣2×3×4×5),
……
n(n+1)(n+2)=[n(n+1)(n+2)(n+3)﹣(n﹣1)n(n+1)(n+2)],
将上述的式子相加得,
1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)=n(n+1)(n+2)(n+3).
21.解:(1)设2020﹣x=a,x﹣2016=b,则(2020﹣x)(x﹣2016)=ab=2,a+b=(2020﹣x)+(x﹣2016)=4,
所以(2020﹣x)2+(x﹣2016)2=a2+b2=(a+b)2﹣2ab=42﹣2×2=12;
故答案为:12;
(2)设2021﹣x=a,x﹣2018=b,则(2021﹣x)2+(x﹣2018)2=a2+b2=2020,a+b=(2021﹣x)+(x﹣2018)=3,
所以(2021﹣x)(x﹣2018)=ab=[(a+b)2﹣(a2+b2)]=×(32﹣2020)=﹣;
答:(2021﹣x)(x﹣2018)的值为﹣;
(3)由题意得,FC=(20﹣x),EC=(12﹣x),
∵长方形CEPF的面积为160,
∴(20﹣x)(12﹣x)=160,
∴(20﹣x)(x﹣12)=﹣160,
∴阴影部分的面积为(20﹣x)2+(12﹣x)2,
设20﹣x=a,x﹣12=b,则(20﹣x)(x﹣12)=ab=﹣160,a+b=(20﹣x)+(x﹣12)=8,
所以(20﹣x)2+(x﹣12)2=(20﹣x)2+(12﹣x)2=a2+b2=(a+b)2﹣2ab=82﹣2×(﹣160)=384;
故答案为:384.
22.解:(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3
=25x2?x7﹣27x9+2x6+x3
=25x9﹣27x9+2x6+x3
=﹣2x9+2x6+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2
=x2﹣4y2﹣2x2﹣6xy+x2+2xy+y2
=﹣3y2﹣4xy.
23.解:原式=x2+xy﹣2x2+2xy+3xy﹣3y2+x2﹣4y2
=6xy﹣7y2,
当x=3,y=﹣1时,原式=6×3×(﹣1)﹣7×(﹣1)2=﹣25.
24.解:(1)①绿化的面积为:(3a+b)(2a+b)﹣(a+b)2﹣a(3a+b﹣a﹣b)
=6a2+5ab+b2﹣a2﹣2ab﹣b2﹣2a2
=(3a2+3ab)平方米;
答:绿化的面积是(3a2+3ab)平方米;
②如图,∵3a2+3ab=3a(a+b),
∴所拼矩形相邻两边的长分别为3a米和(a+b)米;
所以要使所拼矩形面积最大,
3a=a+b,
所以2a=b;
(2)当a=3,b=2,
绿化面积是3a2+3ab=3×9+3×3×2=45(平方米).
25.解:(1)x2﹣8x+7=x2﹣8x+16+7﹣16=(x﹣4)2﹣9
=(x﹣4)2﹣32=(x﹣4+3)(x﹣4﹣3)=(x﹣1)(x﹣7);
(2)x2﹣10xy+9y2=x2﹣10xy+25y2+9y2﹣25y2=(x﹣5y)2﹣16y2
=(x﹣5y)2﹣(4y)2=[(x﹣5y)+4y][(x﹣5y)﹣4y]=(x﹣y)(x﹣9y);
故答案为:25y2,25y2,4y,4y,4y,9y;
(3)原式=x2+[13m+(﹣m)]x+13m?(﹣m)=(x+13m)(x﹣m);
原式=x2+12mx+36m2﹣13m2﹣36m2
=(x+6m)2﹣49m2=(x+6m+7m)(x+6m﹣7m)=(x+13m)(x﹣m).
26.解:(1)观察图形可得:大正方形的边长为:a+b+c,该正方形的面积等于3个小正方形的面积加上6个长方形的面积,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,a+b+c=6,a2+b2+c2=14,
∴62=14+2(ab+ac+bc),
∴ab+ac+bc=(36﹣14)÷2=11.
(3)由题意得:(2a+b)(a+4b)=xa2+yab+zb2,
∴2a2+8ab+ab+4b2=xa2+yab+zb2,
∴2a2+9ab+4b2=xa2+yab+zb2,
∴x=2,y=9,z=4,
∴x+y+z=2+9+4=15.
故答案为:15.
27.解:(1)A=(x+1)2﹣(x2﹣4y)
=x2+2x+1﹣x2+4y
=2x+1+4y;
(2)∵x+2y=1,
由(1)得:A=2x+1+4y=2(x+2y)+1
∴A=2×1+1=3
1.已知a,b,c是△ABC的三条边长,且(a+b+c)(a﹣b)=0,则△ABC一定是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.以上均不对
2.要使(x2﹣x+5)(2x2﹣ax﹣4)展开式中不含x2项,则a的值等于( )
A.﹣6
B.6
C.14
D.﹣14
3.已知x2+x=1,那么x4+2x3﹣x2﹣2x+2020的值为( )
A.2019
B.2020
C.2021
D.2022
4.下列各式:①﹣x2﹣y2;②﹣a2b2+1;
③a2+ab+b2;
④﹣x2+2xy﹣y2;⑤﹣mn+m2n2,用公式法分解因式的有( )
A.2个
B.3个
C.4个
D.5个
5.若a2﹣b2=16,(a+b)2=8,则ab的值为( )
A.﹣
B.
C.﹣6
D.6
6.已知a﹣b=b﹣c=2,a2+b2+c2=11,则ab+bc+ac=( )
A.﹣22
B.﹣1
C.7
D.11
7.已知664﹣1能被30﹣40之间的两个整数整除,则这两个整数是( )
A.35,37
B.35,36
C.34,38
D.36,37
8.下列各项分解因式正确的是( )
A.a2﹣1=(a﹣1)2
B.a2﹣4a+2=(a﹣2)2
C.﹣b2+a2=(a+b)(a﹣b)
D.x2﹣2x﹣3=(x﹣1)(x+3)
9.若x2+5x+m=(x+n)2,则m,n的值分别为( )
A.m=,n=
B.m=,n=5
C.m=25,n=5
D.m=5,n=
10.已知x2﹣2(m+1)xy+16y2是一个完全平方式,则(m2﹣5m﹣14)÷(m+2)=
.
11.若(x+2)(x+a)=x2+bx﹣8,则ab的值为
.
12.如图.现有正方形卡片A类,B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b),宽为(3a+2b)的大长方形,那么需要C类卡片的张数是
.
13.若a﹣b=﹣2,则a2﹣ab+2b=
.
14.如图,边长分别为a,b的两个正方形并排放在一起,当a+b=16,ab=60时阴影部分的面积为
.
15.若x2﹣2x﹣6=0,则(x﹣3)2+(2x+1)(2x﹣1)﹣2x2的值为
.
16.已知4x=10,25y=10,则(x﹣2)(y﹣2)+3(xy﹣1)的值为
.
17.已知a﹣b=5,ab=﹣2,则代数式a2+b2﹣2021的值是
.
18.因式分解:15x2+13xy﹣44y2=
.
19.已知ax2+bx+1与2x2﹣3x+1的积不含x3项,也不含x项,求a与b的值.
20.为探求1×2+2×3+3×4+…+n(n+1)的值,喜欢研究的小明同学发现有下面三个等式:
1×2=(1×2×3﹣0×1×2)
2×3=(2×3×4﹣1×2×3)
3×4=(3×4×5﹣2×3×4)
他将这三个式子相加得到1×2+2×3+3×4=×3×4×5.
请你沿着小明的思路继续研究:
(1)填空:计算1×2+2×3+3×4+…+100×101=
.
计算1×2+2×3+3×4+…+n×(n+1)=
.
(2)利用(1)的规律计算:2×4+4×6+6×8+…+100×102.
(3)继续研究,计算1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)的公式(要求仿照小明的思路写出推导过程).
21.阅读理解:
若x满足(30﹣x)(x﹣10)=160,求(30﹣x)2+(x﹣10)2的值.
解:设30﹣x=a,x﹣10=b,则(30﹣x)(x﹣10)=ab=160,a+b=(30﹣x)+(x﹣10)=20,(30﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=202﹣2×160=80
解决问题:
(1)若x满足(2020﹣x)(x﹣2016)=2.则(2020﹣x)2+(x﹣2016)2=
;
(2)若x满足(2021﹣x)2+(x﹣2018)2=2020,求(2021﹣x)(x﹣2018)的值;
(3)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为
平方单位.
22.计算:
(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2.
23.先化简,再求值:x(x+y)﹣(2x﹣3y)(x﹣y)+(x﹣2y)(x+2y),
其中x=3,y=﹣1.
24.如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.(a>0,b>0)
(1)①试用含a,b的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形,请你求出所拼矩形相邻两边的长;如果要使所拼矩形面积最大,求a与b满足的关系式;
(2)若a=3,b=2,请求出绿化面积.
25.我们知道形如x2+(a+b)x+ab的二次三项式可以分解因式为(x+a)(x+b),
所以x2+6x﹣7=x2+[7+(﹣1)]x+7×(﹣1)=(x+7)[x+(﹣1)]=(x+7)(x﹣1).
但小白在学习中发现,对于x2+6x﹣7还可以使用以下方法分解因式.
x2+6x﹣7=x2+6x+9﹣7﹣9=(x+3)2﹣16=(x+3)2﹣42
=(x+3+4)(x+3﹣4)=(x+7)(x﹣1).
这种在二次三项式x2+6x﹣7中先加上9,使它与x2+6x的和成为一个完全平方式,再减去9,整个式子的值不变,从而可以进一步使用平方差公式继续分解因式了.
(1)请使用小白发现的方法把x2﹣8x+7分解因式;
(2)填空:x2﹣10xy+9y2=x2﹣10xy+
+9y2﹣
=(x﹣5y)2﹣16y2
=(x﹣5y)2﹣(
)2=[(x﹣5y)+
][(x﹣5y)﹣
]
=(x﹣y)(x﹣
);
(3)请用两种不同方法分解因式x2+12mx﹣13m2.
26.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.
例如由图①可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.
请解答下列问题:
(1)写出由图②可以得到的数学等式
;
(2)利用(1)中得到的结论,解决下面问题:若a+b+c=6,a2+b2+c2=14,求ab+bc+ac的值;
(3)可爱同学用图③中x个边长为a的正方形,y个宽为a,长为b的长方形,z个边长为b的正方形,拼出一个面积为(2a+b)(a+4b)的长方形,则x+y+z=
.
27.已知多项式A=(x+1)2﹣(x2﹣4y).
(1)化简多项式A;
(2)若x+2y=1,求A的值.
参考答案
1.解:∵(a+b+c)(a﹣b)=0,
∴a+b+c=0或a﹣b=0,
∵a,b,c是△ABC的三条边长,
∴a+b+c>0,
∴a﹣b=0,即a=b,
∴△ABC一定是等腰三角形.
故选:A.
2.解:(x2﹣x+5)(2x2﹣ax﹣4)
=2x4﹣ax3﹣4x2﹣2x3+ax2+4x+10x2﹣5ax﹣20
=2x4﹣(a+2)x3+(a+6)x2+(4﹣5a)x﹣20,
∵展开式中不含x2项,
∴a+6=0,
∴a=﹣6,
故选:A.
3.解:∵x2+x=1,
∴x4+2x3﹣x2﹣2x+2020=x4+x3+x3﹣x2﹣2x+2020
=x2(x2+x)+x3﹣x2﹣2x+2020=x2+x3﹣x2﹣2x+2020
=x(x2+x)﹣x2﹣2x+2020=x﹣x2﹣2x+2020
=﹣x2﹣x+2020=﹣(x2+x)+2020=﹣1+2020=2019.故选:A.
4.解:①﹣x2﹣y2=﹣(x2+y2),因此①不能用公式法分解因式;
②﹣a2b2+1=1﹣(ab)2=(1+ab)(1﹣ab),因此②能用公式法分解因式;
③a2+ab+b2不符合完全平方公式的结果特征,因此③不能用公式法分解因式;
④﹣x2+2xy﹣y2=﹣(x2﹣2xy+y2)=﹣(x﹣y)2,因此④能用公式法分解因式;
⑤﹣mn+m2n2=(﹣mn)2,因此⑤能用公式法分解因式;
综上所述,能用公式法分解因式的有②④⑤,
故选:B.
5.解:∵a2﹣b2=16,
∴(a+b)(a﹣b)=16,
∴(a+b)2(a﹣b)2=256,
∵(a+b)2=8,
∴(a﹣b)2=32,
∴ab===﹣6,
故选:C.
6.解:∵a﹣b=b﹣c=2,
∴a﹣c=4,
∴a2+b2+c2﹣ab﹣bc﹣ac=(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)=[(a﹣b)2+(b﹣c)2+(c﹣a)2]=12,
∴ab+bc+ac=a2+b2+c2﹣12=﹣1,
故选:B.
7.解:664﹣1=(632+1)(632﹣1)=(632+1)(616+1)(616﹣1)
=(632+1)(616+1)(68+1)(68﹣1)=(632+1)(616+1)(68+1)(64+1)(64﹣1)
=(632+1)(616+1)(68+1)(64+1)(62+1)(62﹣1)
=(632+1)(616+1)(68+1)(64+1)×37×35.
故选:A.
8.解:A、a2﹣1=(a+1)(a﹣1),所以A选项错误;
B、a2﹣4a+2在实数范围内不能因式分解;
C、﹣b2+a2=a2﹣b2=(a+b)(a﹣b),所以C选项正确;
D、x2﹣2x﹣3=(x﹣3)(x+1),所以D选项错误.
故选:C.
9.解:∵x2+5x+m=(x+n)2=x2+2nx+n2,
∴2n=5,m=n2,
解得m=,n=,
故选:A.
10.解:∵x2﹣2(m+1)xy+16y2是一个完全平方式,
∴﹣2(m+1)xy=±2?x?4y,
解得:m=3或﹣5,
(m2﹣5m﹣14)÷(m+2)=(m+2)(m﹣7)÷(m+2)=m﹣7,
当m=3时,原式=3﹣7=﹣4;
当m=﹣5时,原式=﹣5﹣7=﹣12;
故答案为:﹣4或﹣12.
11.解:∵(x+2)(x+a)=x2+(2+a)x+2a,
又∵(x+2)(x+a)=x2+bx﹣8,
∴x2+(2+a)x+2a=x2+bx﹣8.
∴2+a=b,2a=﹣8.
∴a=﹣4,b=﹣2.
∴ab=(﹣4)﹣2==.故答案为:.
12.解:∵(a+3b)(3a+2b)=3a2+11ab+6b2,
∵一张C类卡片的面积为ab,
∴需要C类卡片11张.
故答案为:11.
13.解:∵a﹣b=﹣2,
∴a2﹣ab+2b=a(a﹣b)+2b=﹣2a+2b=﹣2(a﹣b)=4.
故答案为:4.
14.解:根据题意得:S阴影部分=a2+b2﹣a2﹣b(a+b)=a2+b2﹣a2﹣ab﹣b2
=(a2+b2﹣ab)=[(a+b)2﹣3ab],
把a+b=16,ab=60代入得:S阴影部分=38.
故图中阴影部分的面积为38.
故答案为38.
15.解:∵x2﹣2x﹣6=0,
∴x2﹣2x=6,
∴(x﹣3)2+(2x+1)(2x﹣1)﹣2x2=x2﹣6x+9+4x2﹣1﹣2x2=3x2﹣6x+8
=3(x2﹣2x)+8=3×6+8=26,
故答案为:26.
16.解:∵,
∴由①得4xy=10y,③
由②得25xy=10x,④
∴③×④得4xy?25xy=10y?10x,即(4×25)xy=10x+y,
∴(102)xy=10x+y,
∴102xy=10x+y,
∴2xy=x+y
(x﹣2)(y﹣2)+3(xy﹣1)=xy﹣2x﹣2y+4+3xy﹣3=4xy﹣2(x+y)+1
=4xy﹣2×2xy+1=1.故答案为:1.
17.解:a2+b2﹣2021=(a﹣b)2+2ab﹣2021=52﹣4﹣2021=-2001.故答案为:-2001
18.解:利用十字相乘法,如图,
将二次项系数、常数项分别分解,交叉乘加验中项,得出答案,
15x2+13xy﹣44y2=(3x﹣4y)(5x+11y).
故答案为:(3x﹣4y)(5x+11y).
19.解:根据题意列得:(ax2+bx+1)(2x2﹣3x+1)=2ax4+(2b﹣3a)x3+(a+2﹣3b)x2+(b﹣3)x+1,
∵不含x3的项,也不含x的项,
∴2b﹣3a=0,b﹣3=0,
解得a=2,b=3.
20.解:(1)1×2+2×3+3×4+…+100×101=(100×101×102)=343400,
1×2+2×3+3×4+…+n×(n+1)=n×(n+1)(n+2),
故答案为:343400,n(n+1)(n+2);
(2)仿照上述的方法可得,
2×4=(2×4×6﹣0×2×4),
4×6=(4×6×8﹣2×4×6),
6×8=(6×8×10﹣4×6×8),
……
100×102=(100×102×104﹣98×100×102),
将上式相加得,
2×4+4×6+6×8+…+100×102=(100×102×104)=176800;
(3)仿照上述的方法可得,
1×2×3=(1×2×3×4﹣0×1×2×3),
2×3×4=(2×3×4×5﹣1×2×3×4),
3×4×5=(3×4×5×6﹣2×3×4×5),
……
n(n+1)(n+2)=[n(n+1)(n+2)(n+3)﹣(n﹣1)n(n+1)(n+2)],
将上述的式子相加得,
1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)=n(n+1)(n+2)(n+3).
21.解:(1)设2020﹣x=a,x﹣2016=b,则(2020﹣x)(x﹣2016)=ab=2,a+b=(2020﹣x)+(x﹣2016)=4,
所以(2020﹣x)2+(x﹣2016)2=a2+b2=(a+b)2﹣2ab=42﹣2×2=12;
故答案为:12;
(2)设2021﹣x=a,x﹣2018=b,则(2021﹣x)2+(x﹣2018)2=a2+b2=2020,a+b=(2021﹣x)+(x﹣2018)=3,
所以(2021﹣x)(x﹣2018)=ab=[(a+b)2﹣(a2+b2)]=×(32﹣2020)=﹣;
答:(2021﹣x)(x﹣2018)的值为﹣;
(3)由题意得,FC=(20﹣x),EC=(12﹣x),
∵长方形CEPF的面积为160,
∴(20﹣x)(12﹣x)=160,
∴(20﹣x)(x﹣12)=﹣160,
∴阴影部分的面积为(20﹣x)2+(12﹣x)2,
设20﹣x=a,x﹣12=b,则(20﹣x)(x﹣12)=ab=﹣160,a+b=(20﹣x)+(x﹣12)=8,
所以(20﹣x)2+(x﹣12)2=(20﹣x)2+(12﹣x)2=a2+b2=(a+b)2﹣2ab=82﹣2×(﹣160)=384;
故答案为:384.
22.解:(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3
=25x2?x7﹣27x9+2x6+x3
=25x9﹣27x9+2x6+x3
=﹣2x9+2x6+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2
=x2﹣4y2﹣2x2﹣6xy+x2+2xy+y2
=﹣3y2﹣4xy.
23.解:原式=x2+xy﹣2x2+2xy+3xy﹣3y2+x2﹣4y2
=6xy﹣7y2,
当x=3,y=﹣1时,原式=6×3×(﹣1)﹣7×(﹣1)2=﹣25.
24.解:(1)①绿化的面积为:(3a+b)(2a+b)﹣(a+b)2﹣a(3a+b﹣a﹣b)
=6a2+5ab+b2﹣a2﹣2ab﹣b2﹣2a2
=(3a2+3ab)平方米;
答:绿化的面积是(3a2+3ab)平方米;
②如图,∵3a2+3ab=3a(a+b),
∴所拼矩形相邻两边的长分别为3a米和(a+b)米;
所以要使所拼矩形面积最大,
3a=a+b,
所以2a=b;
(2)当a=3,b=2,
绿化面积是3a2+3ab=3×9+3×3×2=45(平方米).
25.解:(1)x2﹣8x+7=x2﹣8x+16+7﹣16=(x﹣4)2﹣9
=(x﹣4)2﹣32=(x﹣4+3)(x﹣4﹣3)=(x﹣1)(x﹣7);
(2)x2﹣10xy+9y2=x2﹣10xy+25y2+9y2﹣25y2=(x﹣5y)2﹣16y2
=(x﹣5y)2﹣(4y)2=[(x﹣5y)+4y][(x﹣5y)﹣4y]=(x﹣y)(x﹣9y);
故答案为:25y2,25y2,4y,4y,4y,9y;
(3)原式=x2+[13m+(﹣m)]x+13m?(﹣m)=(x+13m)(x﹣m);
原式=x2+12mx+36m2﹣13m2﹣36m2
=(x+6m)2﹣49m2=(x+6m+7m)(x+6m﹣7m)=(x+13m)(x﹣m).
26.解:(1)观察图形可得:大正方形的边长为:a+b+c,该正方形的面积等于3个小正方形的面积加上6个长方形的面积,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,a+b+c=6,a2+b2+c2=14,
∴62=14+2(ab+ac+bc),
∴ab+ac+bc=(36﹣14)÷2=11.
(3)由题意得:(2a+b)(a+4b)=xa2+yab+zb2,
∴2a2+8ab+ab+4b2=xa2+yab+zb2,
∴2a2+9ab+4b2=xa2+yab+zb2,
∴x=2,y=9,z=4,
∴x+y+z=2+9+4=15.
故答案为:15.
27.解:(1)A=(x+1)2﹣(x2﹣4y)
=x2+2x+1﹣x2+4y
=2x+1+4y;
(2)∵x+2y=1,
由(1)得:A=2x+1+4y=2(x+2y)+1
∴A=2×1+1=3
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
