2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》章末综合提升训练(word版含解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第9章整式乘法与因式分解》章末综合提升训练(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览



文档简介
2021年苏科版七年级数学下册《第9章整式乘法与因式分解》章末综合提升训练(附答案)
1.计算:
(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2.
2.定义一种新运算:观察下列各式:
1⊙3=1×4+3=7,
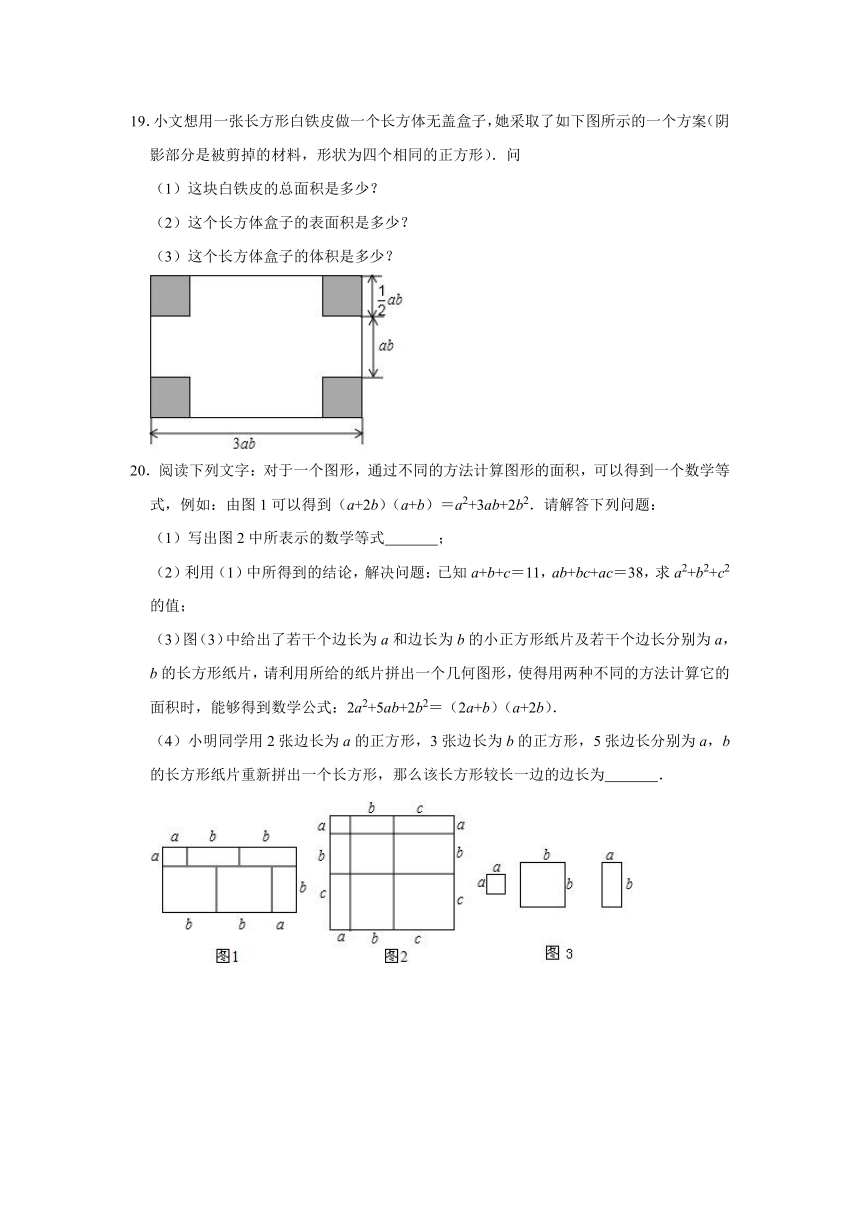
3⊙(﹣1)=3×4﹣1=11,
5⊙4=5×4+4=24,
4⊙(﹣3)=4×4﹣3=13.
(1)请你想一想:a⊙b=
;
(2)若a≠b,那么a⊙b
b⊙a(填“=”或“≠”);
(3)先化简,再求值:(a﹣b)⊙(2a+b),其中a=﹣1,b=2.
3.如图,边长分别为a,b的两个正方形并排放在一起,请计算图中阴影部分面积,并求出当a+b=16,ab=60时阴影部分的面积.
4.计算:
(1)(﹣x2y)3+7(x2)2?(﹣x)2?(﹣y)3;
(2)(x+3)(x+4)﹣(x﹣1)2.
5.x(x﹣3)(﹣3﹣x)﹣2(﹣x﹣1)2+(x﹣2)(x2﹣3).
6.化简(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2
7.计算
(1)(﹣2x4y3z)2?8x4y2÷(﹣15x2y2)
(2)(x+3y﹣2)(x﹣3y﹣2)
(3)(x+4)2﹣(x+2)(x﹣5)
(4)(3ab+4)2﹣(3ab﹣4)2
(5)(3a﹣b)2﹣(2a+b)2﹣5a(a﹣b)
(6)(a﹣2b)(a+2b)(a2﹣4b2)
8.计算题
(1)(2x2y)3?(﹣7xy2);
(2)(2a+1)2﹣(2a+1)(﹣1+2a);
(3)(x﹣2y+4)(x+2y﹣4);
(4)20202﹣2022×2018(用乘法公式计算).
9.计算:(a+b)2+(a﹣b)(2a+b)﹣3(a+b)(a﹣b)
10.先阅读小亮解答的问题(1),再仿照他的方法解答问题(2)
问题(1):计算3.1468×7.1468﹣0.14682
小亮的解答如下:
解:设0.1468=a,则3.1468=a+3,7.1468=a+7
原式=(a+3)(a+7)﹣a2
=a2+10a+21﹣a2
=10a+21
把a=0.1468代入
原式=10×0.1468+21=22,468
∴3.1468×7.1468﹣0.14682=22.468
问题(2):计算:67897×67898﹣67896×67899.
11.计算:
(1)4x2﹣(﹣2x+3)(﹣2x﹣3)
(2)(x+2y)2﹣(x+y)(3x﹣y)﹣5y2.
12.计算
(1)a4?(﹣a3)2÷(﹣a2)5
(2)9m4(n2)3+(﹣3m2n3)2
(3)(3x2+2x+1)(3x﹣1)
(4)(45a3﹣a2b+3a)÷(﹣a)
(5)(1﹣3y)(1+3y)(1+9y2)
(6)(3a+b+c)(3a+b﹣c)
13.计算:
(1)(ab2)2?(﹣a3b)3÷(﹣4a3b2)
(2)m(3m2﹣4m+5)﹣m(4m+3)
(3)(2x+y﹣3)2
(4)(4x﹣3y+2)(4x+3y+2)
14.(1)化简:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2.
(2)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
15.观察下列关于自然数的等式:
(1)32﹣4×12=5
(1)
(2)52﹣4×22=9
(2)
(3)72﹣4×32=13
(3)…
根据上述规律解决下列问题:
(1)完成第五个等式:112﹣4×
2=
;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
16.计算:
(1)2x3y?(﹣2xy)+(﹣2x2y)2
(2)3b(b﹣2a3)﹣(9ab3+12a4b2)÷(3ab)
(3)(2x﹣3y)2﹣(y+3x)(x﹣3y)
(4)运用乘法公式简化计算:2021×2023﹣20222
(5)(5m+6n+p)(5m﹣6n+p)
17.计算
(1)(2x2y3)﹣3x4y3?(﹣x2);
(2)(a4b7﹣a2b6)÷(﹣ab3)2
(3)(x+y)2﹣(x﹣y)(﹣x﹣y)
(4)(a﹣b+2c)(a+b﹣2c)
18.计算:
(1)(﹣2x3y)2?(﹣2xy)+(﹣2x3y)3÷2x2
(2)20202﹣2019×2021
(3)(﹣2a+b+1)(2a+b﹣1)
19.小文想用一张长方形白铁皮做一个长方体无盖盒子,她采取了如下图所示的一个方案(阴影部分是被剪掉的材料,形状为四个相同的正方形).问
(1)这块白铁皮的总面积是多少?
(2)这个长方体盒子的表面积是多少?
(3)这个长方体盒子的体积是多少?
20.阅读下列文字:对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如:由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式
;
(2)利用(1)中所得到的结论,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图(3)中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a,b的长方形纸片,请利用所给的纸片拼出一个几何图形,使得用两种不同的方法计算它的面积时,能够得到数学公式:2a2+5ab+2b2=(2a+b)(a+2b).
(4)小明同学用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长一边的边长为
.
参考答案
1.解:(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3
=25x2?x7﹣27x9+2x6+x3=25x9﹣27x9+2x6+x3=﹣2x9+2x6+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2
=x2﹣4y2﹣2x2﹣6xy+x2+2xy+y2=﹣3y2﹣4xy.
2.解:(1)由题意可得,
a⊙b=4a+b,
故答案为:4a+b;
(2)由题意可得,
a⊙b﹣b⊙a
=(4a+b)﹣(4b+a)
=4a+b﹣4b﹣a
=3(a﹣b),
∵a≠b,
∴3(a﹣b)≠0,
∴a⊙b≠b⊙a,
故答案为:≠;
(3)由题意可得,
(a﹣b)⊙(2a+b)=4(a﹣b)+(2a+b)=4a﹣4b+2a+b=6a﹣3b,
当a=﹣1,b=2时,原式=6×(﹣1)﹣3×2=﹣6﹣6=﹣12.
3.解:根据题意得:S阴影部分=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣a2﹣ab﹣b2=(a2+b2﹣ab)=[(a+b)2﹣3ab],
把a+b=16,ab=60代入得:S阴影部分=38.
故图中阴影部分的面积为38.
4.解:(1)原式=﹣x6y3+7x4?x2?(﹣y3)=﹣x6y3﹣7x6y3=﹣8x6y3;
(2)原式=x2+4x+3x+12﹣x2+2x﹣1=9x+11.
5.解:原式=x(9﹣x2)﹣2(x2+2x+1)+x3﹣3x﹣2x2+6
=9x﹣x3﹣2x2﹣4x﹣2+x3﹣3x﹣2x2+6=﹣4x2+2x+4.
6.解:原式=x2﹣4y2﹣2x2﹣6xy+x2+2xy+y2=﹣3y2﹣4xy
7.解:(1)原式=(4x8y6z2)?8x4y2÷(﹣15x2y2)=﹣x10y6z2;
(2)原式=(x﹣2)2﹣(3y)2=x2﹣4x+4﹣9y2;
(3)原式=x2+8x+16﹣(x2﹣3x﹣10)=x2+8x+16﹣x2+3x+10=11x+26;
(4)原式=(3ab+4+3ab﹣4)(3ab+4﹣3ab+4)=48ab;
(5)原式=9a2﹣6ab+b2﹣4a2﹣4ab﹣b2﹣5a2+5ab=﹣5ab;
(6)原式=(a2﹣4b2)(a2﹣4b2)=(a2﹣4b2)2=a4﹣8a2b2+16b4.
8.解:(1)(2x2y)3?(﹣7xy2)=8x6y3?(﹣7xy2)=﹣56x7y5;
(2)(2a+1)2﹣(2a+1)(﹣1+2a)=4a2+4a+1﹣4a2+1=4a+2;
(3)(x﹣2y+4)(x+2y﹣4)=[x﹣(2y﹣4)][x+(2y﹣4)]
=x2﹣(2y﹣4)2=x2﹣4y2+16y﹣16;
(4)20202﹣2022×2018
=20202﹣(2020+2)×(2020﹣2)=20202﹣20202+4=4.
9.解:原式=a2+2ab+b2+2a2+ab﹣2ab﹣b2﹣3a2+3b2=ab+3b2.
10.解:设67897=a,则67898=a+1,67896=a﹣1,67899=a+2,
则67897×67898﹣67896×67899
=a(a+1)﹣(a﹣1)(a+2)=(a2+a)﹣(a2+a﹣2)=a2+a﹣a2﹣a+2
=2.
11.解:(1)4x2﹣(﹣2x+3)(﹣2x﹣3)=4x2﹣(4x2﹣9)=4x2﹣4x2+9=9;
(2)(x+2y)2﹣(x+y)(3x﹣y)﹣5y2
=x2+4xy+4y2﹣3x2+xy﹣3xy+y2﹣5y2=﹣2x2+2xy.
12.解:(1)原式=﹣a4?a6÷a10=﹣1;
(2)原式=9m4n6+9m4n6=18m4n6;
(3)原式=9x3﹣3x2+3x﹣3x2﹣2x﹣1=9x3﹣6x2+x﹣1;
(4)原式=﹣135a2+ab﹣9;
(5)原式=(1﹣9y2)(1+9y2)=1﹣81y4;
(6)原式=(3a+b)2﹣c2=9a2+6ab+b2﹣c2.
13.解:(1)原式=a2b4?(﹣a9b3)÷(﹣4a3b2)=﹣a11b7÷(﹣4a3b2)=a8b5;
(2)原式=2m3﹣m2+m﹣6m2﹣3m=2m3﹣m2﹣m;
(3)原式=(2x+y)2﹣6(2x+y)+9=4x2+4xy+y2﹣﹣12x﹣6y+9;
(4)原式=(4x+2)2﹣(3y)2=16x2+16x+4﹣9y2.
14.解:(1)原式=4﹣a2+a2﹣5ab+3a5b3÷a4b2=4﹣5ab+3ab=4﹣2ab.
(2)∵(x+y)2=25,(x﹣y)2=9,
所以x2+2xy+y2=25①,
x2﹣2xy+y2=9②.
①+②,得
2(x2+y2)=34,
即x2+y2=17;
①﹣②,得
4xy=16
即xy=4.
所以xy=4,x2+y2=17.
15.解:(1)112﹣4×52=21,
故答案为:5;21;
(2)第n个等式为:(2n+1)2﹣4n2=4n+1,
证明:(2n+1)2﹣4n2=4n2+4n+1﹣4n2=4n+1.
16.解:(1)2x3y?(﹣2xy)+(﹣2x2y)2=﹣4x4y2+4x4y2=0;
(2)3b(b﹣2a3)﹣(9ab3+12a4b2)÷(3ab)=3b2﹣6a3b﹣3b2﹣4a3b=﹣10a3b;
(3)(2x﹣3y)2﹣(y+3x)(x﹣3y)=4x2﹣12xy+9y2﹣xy+3y2﹣3x2+9xy=x2﹣4xy+12y2;
(4)2021×2023﹣20222=(2022﹣1)(2022+1)﹣20222=20222﹣1﹣20222=﹣1;
(5)(5m+6n+p)(5m﹣6n+p)=[(5m+p)+6n][(5m+p)﹣6n]
=(5m+p)2﹣36n2=25m2+10mp+p2﹣36n2.
17.解:(1)(2x2y3)﹣3x4y3?(﹣x2)=2x2y3+3x6y3;
(2)(a4b7﹣a2b6)÷(﹣ab3)2=(a4b7﹣a2b6)÷a2b6=6a2b﹣1;
(3)(x+y)2﹣(x﹣y)(﹣x﹣y)=(x2+2xy+y2)﹣(y2﹣x2)=x2+2xy+y2﹣y2+x2=2x2+2xy;
(4)(a﹣b+2c)(a+b﹣2c)=[a﹣(b﹣2c)][a+(b﹣2c)]
=a2﹣(b﹣2c)2=a2﹣b2+4bc﹣4c2.
18.解:(1)原式=4x6y2?(﹣2xy)+(﹣8x9y3)÷2x2=﹣8x7y3+(﹣4x7y3)=﹣12x7y3;
(2)20202﹣2019×2021=20202﹣(2020﹣1)×(2020+1)=20202﹣20202+1=1;
(3)(﹣2a+b+1)(2a+b﹣1)=[b﹣(2a﹣1)][b+(2a﹣1)]
=b2﹣(2a﹣1)2=b2﹣4a2+4a﹣1.
19.解:(1)这张白铁皮的面积为3ab(ab+2×ab)=3ab×2ab=6a2b2;
(2)这个长方体盒子的表面积是6a2b2﹣4×(ab)2=6a2b2﹣a2b2=5a2b2;
(3)这个长方体盒子的体积是(3ab﹣2×ab)?ab?ab
=2ab?ab?ab
=a3b3.
20.解:(1)根据题意得:(a+b+c)(a+b+c)=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc=121﹣76=45;
(3)画出相应的图形,如图所示;
(4)∵2a2+5ab+3b2=(2a+3b)(a+b),
∴该长方形较长一边的边长为2a+3b.
故答案为:(1)(a+b+c)(a+b+c)=a2+b2+c2+2ab+2ac+2bc;(4)2a+3b
1.计算:
(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2.
2.定义一种新运算:观察下列各式:
1⊙3=1×4+3=7,
3⊙(﹣1)=3×4﹣1=11,
5⊙4=5×4+4=24,
4⊙(﹣3)=4×4﹣3=13.
(1)请你想一想:a⊙b=
;
(2)若a≠b,那么a⊙b
b⊙a(填“=”或“≠”);
(3)先化简,再求值:(a﹣b)⊙(2a+b),其中a=﹣1,b=2.
3.如图,边长分别为a,b的两个正方形并排放在一起,请计算图中阴影部分面积,并求出当a+b=16,ab=60时阴影部分的面积.
4.计算:
(1)(﹣x2y)3+7(x2)2?(﹣x)2?(﹣y)3;
(2)(x+3)(x+4)﹣(x﹣1)2.
5.x(x﹣3)(﹣3﹣x)﹣2(﹣x﹣1)2+(x﹣2)(x2﹣3).
6.化简(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2
7.计算
(1)(﹣2x4y3z)2?8x4y2÷(﹣15x2y2)
(2)(x+3y﹣2)(x﹣3y﹣2)
(3)(x+4)2﹣(x+2)(x﹣5)
(4)(3ab+4)2﹣(3ab﹣4)2
(5)(3a﹣b)2﹣(2a+b)2﹣5a(a﹣b)
(6)(a﹣2b)(a+2b)(a2﹣4b2)
8.计算题
(1)(2x2y)3?(﹣7xy2);
(2)(2a+1)2﹣(2a+1)(﹣1+2a);
(3)(x﹣2y+4)(x+2y﹣4);
(4)20202﹣2022×2018(用乘法公式计算).
9.计算:(a+b)2+(a﹣b)(2a+b)﹣3(a+b)(a﹣b)
10.先阅读小亮解答的问题(1),再仿照他的方法解答问题(2)
问题(1):计算3.1468×7.1468﹣0.14682
小亮的解答如下:
解:设0.1468=a,则3.1468=a+3,7.1468=a+7
原式=(a+3)(a+7)﹣a2
=a2+10a+21﹣a2
=10a+21
把a=0.1468代入
原式=10×0.1468+21=22,468
∴3.1468×7.1468﹣0.14682=22.468
问题(2):计算:67897×67898﹣67896×67899.
11.计算:
(1)4x2﹣(﹣2x+3)(﹣2x﹣3)
(2)(x+2y)2﹣(x+y)(3x﹣y)﹣5y2.
12.计算
(1)a4?(﹣a3)2÷(﹣a2)5
(2)9m4(n2)3+(﹣3m2n3)2
(3)(3x2+2x+1)(3x﹣1)
(4)(45a3﹣a2b+3a)÷(﹣a)
(5)(1﹣3y)(1+3y)(1+9y2)
(6)(3a+b+c)(3a+b﹣c)
13.计算:
(1)(ab2)2?(﹣a3b)3÷(﹣4a3b2)
(2)m(3m2﹣4m+5)﹣m(4m+3)
(3)(2x+y﹣3)2
(4)(4x﹣3y+2)(4x+3y+2)
14.(1)化简:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2.
(2)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
15.观察下列关于自然数的等式:
(1)32﹣4×12=5
(1)
(2)52﹣4×22=9
(2)
(3)72﹣4×32=13
(3)…
根据上述规律解决下列问题:
(1)完成第五个等式:112﹣4×
2=
;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
16.计算:
(1)2x3y?(﹣2xy)+(﹣2x2y)2
(2)3b(b﹣2a3)﹣(9ab3+12a4b2)÷(3ab)
(3)(2x﹣3y)2﹣(y+3x)(x﹣3y)
(4)运用乘法公式简化计算:2021×2023﹣20222
(5)(5m+6n+p)(5m﹣6n+p)
17.计算
(1)(2x2y3)﹣3x4y3?(﹣x2);
(2)(a4b7﹣a2b6)÷(﹣ab3)2
(3)(x+y)2﹣(x﹣y)(﹣x﹣y)
(4)(a﹣b+2c)(a+b﹣2c)
18.计算:
(1)(﹣2x3y)2?(﹣2xy)+(﹣2x3y)3÷2x2
(2)20202﹣2019×2021
(3)(﹣2a+b+1)(2a+b﹣1)
19.小文想用一张长方形白铁皮做一个长方体无盖盒子,她采取了如下图所示的一个方案(阴影部分是被剪掉的材料,形状为四个相同的正方形).问
(1)这块白铁皮的总面积是多少?
(2)这个长方体盒子的表面积是多少?
(3)这个长方体盒子的体积是多少?
20.阅读下列文字:对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如:由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式
;
(2)利用(1)中所得到的结论,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图(3)中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a,b的长方形纸片,请利用所给的纸片拼出一个几何图形,使得用两种不同的方法计算它的面积时,能够得到数学公式:2a2+5ab+2b2=(2a+b)(a+2b).
(4)小明同学用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长一边的边长为
.
参考答案
1.解:(1)(5x)2?x7﹣(3x3)3+2(x3)2+x3
=25x2?x7﹣27x9+2x6+x3=25x9﹣27x9+2x6+x3=﹣2x9+2x6+x3;
(2)(x+2y)(x﹣2y)﹣2x(x+3y)+(x+y)2
=x2﹣4y2﹣2x2﹣6xy+x2+2xy+y2=﹣3y2﹣4xy.
2.解:(1)由题意可得,
a⊙b=4a+b,
故答案为:4a+b;
(2)由题意可得,
a⊙b﹣b⊙a
=(4a+b)﹣(4b+a)
=4a+b﹣4b﹣a
=3(a﹣b),
∵a≠b,
∴3(a﹣b)≠0,
∴a⊙b≠b⊙a,
故答案为:≠;
(3)由题意可得,
(a﹣b)⊙(2a+b)=4(a﹣b)+(2a+b)=4a﹣4b+2a+b=6a﹣3b,
当a=﹣1,b=2时,原式=6×(﹣1)﹣3×2=﹣6﹣6=﹣12.
3.解:根据题意得:S阴影部分=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣a2﹣ab﹣b2=(a2+b2﹣ab)=[(a+b)2﹣3ab],
把a+b=16,ab=60代入得:S阴影部分=38.
故图中阴影部分的面积为38.
4.解:(1)原式=﹣x6y3+7x4?x2?(﹣y3)=﹣x6y3﹣7x6y3=﹣8x6y3;
(2)原式=x2+4x+3x+12﹣x2+2x﹣1=9x+11.
5.解:原式=x(9﹣x2)﹣2(x2+2x+1)+x3﹣3x﹣2x2+6
=9x﹣x3﹣2x2﹣4x﹣2+x3﹣3x﹣2x2+6=﹣4x2+2x+4.
6.解:原式=x2﹣4y2﹣2x2﹣6xy+x2+2xy+y2=﹣3y2﹣4xy
7.解:(1)原式=(4x8y6z2)?8x4y2÷(﹣15x2y2)=﹣x10y6z2;
(2)原式=(x﹣2)2﹣(3y)2=x2﹣4x+4﹣9y2;
(3)原式=x2+8x+16﹣(x2﹣3x﹣10)=x2+8x+16﹣x2+3x+10=11x+26;
(4)原式=(3ab+4+3ab﹣4)(3ab+4﹣3ab+4)=48ab;
(5)原式=9a2﹣6ab+b2﹣4a2﹣4ab﹣b2﹣5a2+5ab=﹣5ab;
(6)原式=(a2﹣4b2)(a2﹣4b2)=(a2﹣4b2)2=a4﹣8a2b2+16b4.
8.解:(1)(2x2y)3?(﹣7xy2)=8x6y3?(﹣7xy2)=﹣56x7y5;
(2)(2a+1)2﹣(2a+1)(﹣1+2a)=4a2+4a+1﹣4a2+1=4a+2;
(3)(x﹣2y+4)(x+2y﹣4)=[x﹣(2y﹣4)][x+(2y﹣4)]
=x2﹣(2y﹣4)2=x2﹣4y2+16y﹣16;
(4)20202﹣2022×2018
=20202﹣(2020+2)×(2020﹣2)=20202﹣20202+4=4.
9.解:原式=a2+2ab+b2+2a2+ab﹣2ab﹣b2﹣3a2+3b2=ab+3b2.
10.解:设67897=a,则67898=a+1,67896=a﹣1,67899=a+2,
则67897×67898﹣67896×67899
=a(a+1)﹣(a﹣1)(a+2)=(a2+a)﹣(a2+a﹣2)=a2+a﹣a2﹣a+2
=2.
11.解:(1)4x2﹣(﹣2x+3)(﹣2x﹣3)=4x2﹣(4x2﹣9)=4x2﹣4x2+9=9;
(2)(x+2y)2﹣(x+y)(3x﹣y)﹣5y2
=x2+4xy+4y2﹣3x2+xy﹣3xy+y2﹣5y2=﹣2x2+2xy.
12.解:(1)原式=﹣a4?a6÷a10=﹣1;
(2)原式=9m4n6+9m4n6=18m4n6;
(3)原式=9x3﹣3x2+3x﹣3x2﹣2x﹣1=9x3﹣6x2+x﹣1;
(4)原式=﹣135a2+ab﹣9;
(5)原式=(1﹣9y2)(1+9y2)=1﹣81y4;
(6)原式=(3a+b)2﹣c2=9a2+6ab+b2﹣c2.
13.解:(1)原式=a2b4?(﹣a9b3)÷(﹣4a3b2)=﹣a11b7÷(﹣4a3b2)=a8b5;
(2)原式=2m3﹣m2+m﹣6m2﹣3m=2m3﹣m2﹣m;
(3)原式=(2x+y)2﹣6(2x+y)+9=4x2+4xy+y2﹣﹣12x﹣6y+9;
(4)原式=(4x+2)2﹣(3y)2=16x2+16x+4﹣9y2.
14.解:(1)原式=4﹣a2+a2﹣5ab+3a5b3÷a4b2=4﹣5ab+3ab=4﹣2ab.
(2)∵(x+y)2=25,(x﹣y)2=9,
所以x2+2xy+y2=25①,
x2﹣2xy+y2=9②.
①+②,得
2(x2+y2)=34,
即x2+y2=17;
①﹣②,得
4xy=16
即xy=4.
所以xy=4,x2+y2=17.
15.解:(1)112﹣4×52=21,
故答案为:5;21;
(2)第n个等式为:(2n+1)2﹣4n2=4n+1,
证明:(2n+1)2﹣4n2=4n2+4n+1﹣4n2=4n+1.
16.解:(1)2x3y?(﹣2xy)+(﹣2x2y)2=﹣4x4y2+4x4y2=0;
(2)3b(b﹣2a3)﹣(9ab3+12a4b2)÷(3ab)=3b2﹣6a3b﹣3b2﹣4a3b=﹣10a3b;
(3)(2x﹣3y)2﹣(y+3x)(x﹣3y)=4x2﹣12xy+9y2﹣xy+3y2﹣3x2+9xy=x2﹣4xy+12y2;
(4)2021×2023﹣20222=(2022﹣1)(2022+1)﹣20222=20222﹣1﹣20222=﹣1;
(5)(5m+6n+p)(5m﹣6n+p)=[(5m+p)+6n][(5m+p)﹣6n]
=(5m+p)2﹣36n2=25m2+10mp+p2﹣36n2.
17.解:(1)(2x2y3)﹣3x4y3?(﹣x2)=2x2y3+3x6y3;
(2)(a4b7﹣a2b6)÷(﹣ab3)2=(a4b7﹣a2b6)÷a2b6=6a2b﹣1;
(3)(x+y)2﹣(x﹣y)(﹣x﹣y)=(x2+2xy+y2)﹣(y2﹣x2)=x2+2xy+y2﹣y2+x2=2x2+2xy;
(4)(a﹣b+2c)(a+b﹣2c)=[a﹣(b﹣2c)][a+(b﹣2c)]
=a2﹣(b﹣2c)2=a2﹣b2+4bc﹣4c2.
18.解:(1)原式=4x6y2?(﹣2xy)+(﹣8x9y3)÷2x2=﹣8x7y3+(﹣4x7y3)=﹣12x7y3;
(2)20202﹣2019×2021=20202﹣(2020﹣1)×(2020+1)=20202﹣20202+1=1;
(3)(﹣2a+b+1)(2a+b﹣1)=[b﹣(2a﹣1)][b+(2a﹣1)]
=b2﹣(2a﹣1)2=b2﹣4a2+4a﹣1.
19.解:(1)这张白铁皮的面积为3ab(ab+2×ab)=3ab×2ab=6a2b2;
(2)这个长方体盒子的表面积是6a2b2﹣4×(ab)2=6a2b2﹣a2b2=5a2b2;
(3)这个长方体盒子的体积是(3ab﹣2×ab)?ab?ab
=2ab?ab?ab
=a3b3.
20.解:(1)根据题意得:(a+b+c)(a+b+c)=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc=121﹣76=45;
(3)画出相应的图形,如图所示;
(4)∵2a2+5ab+3b2=(2a+3b)(a+b),
∴该长方形较长一边的边长为2a+3b.
故答案为:(1)(a+b+c)(a+b+c)=a2+b2+c2+2ab+2ac+2bc;(4)2a+3b
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
