人教版数学七年级下册:7.2.2 用坐标表示平移 同步练习(word附答案)
文档属性
| 名称 | 人教版数学七年级下册:7.2.2 用坐标表示平移 同步练习(word附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-10 00:00:00 | ||
图片预览




文档简介
7.2.2 用坐标表示平移
1.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2)
C.(5,2) D.(3,4)
2.将点A(-2,-3)向左平移3个单位长度得到点B,则点B的坐标是( )
A.(1,-3) B.(-2,0)
C.(-5,-3) D.(-2,-6)
3.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是 .
4.平面直角坐标系中,将三角形各点的纵坐标都减去-3,横坐标保持不变,所得图形与原图形相比( )
A.向上平移了3个单位长度
B.向下平移了3个单位长度
C.向右平移了3个单位长度
D.向左平移了3个单位长度
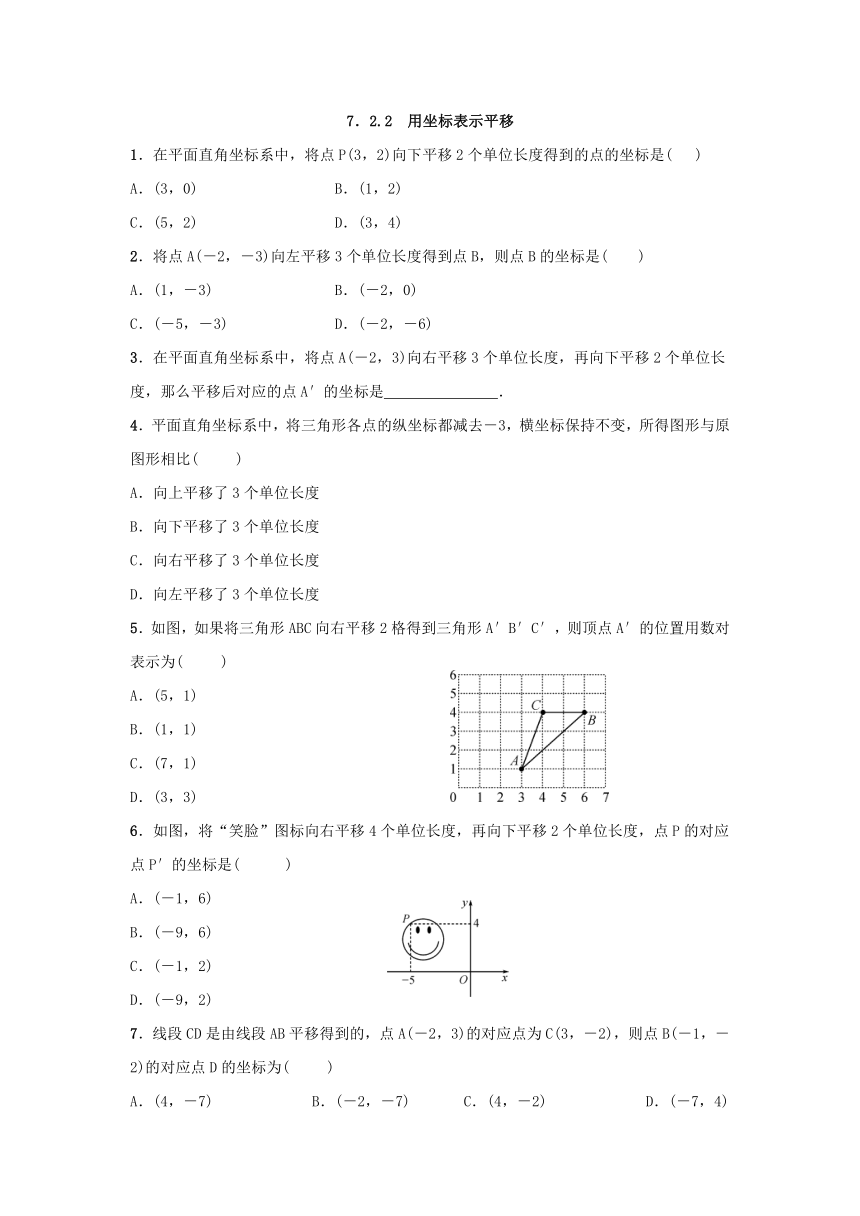
28130505264155.如图,如果将三角形ABC向右平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
A.(5,1)
B.(1,1)
C.(7,1)
D.(3,3)
6.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,点P的对应点P′的坐标是( )
2264410167640A.(-1,6)
B.(-9,6)
C.(-1,2)
D.(-9,2)
7.线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,-2),则点B(-1,-2)的对应点D的坐标为( )
A.(4,-7) B.(-2,-7) C.(4,-2) D.(-7,4)
8.如图所示:
(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;
(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图形,并写出平移后7个对应点的坐标.
9.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是 .
10.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
253873080010011.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a-2,b+3)
B.(a-2,b-3)
C.(a+2,b+3)
D.(a+2,b-3)
12.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m= .
13.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;
(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.
413131083820
14.如图,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A′B′C′.
(1)在图中画出三角形A′B′C′;
(2)写出点A′,B′的坐标;
(3)求三角形A′B′C′的面积;
(4)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
15.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为点A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
参考答案:
7.2.2 用坐标表示平移
1.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是(A)
A.(3,0) B.(1,2)
C.(5,2) D.(3,4)
2.将点A(-2,-3)向左平移3个单位长度得到点B,则点B的坐标是(C)
A.(1,-3) B.(-2,0)
C.(-5,-3) D.(-2,-6)
3.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是(1,1).
4.平面直角坐标系中,将三角形各点的纵坐标都减去-3,横坐标保持不变,所得图形与原图形相比(A)
A.向上平移了3个单位长度
B.向下平移了3个单位长度
C.向右平移了3个单位长度
D.向左平移了3个单位长度
5.如图,如果将三角形ABC向右平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为(A)
A.(5,1) B.(1,1)
C.(7,1) D.(3,3)
6.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,点P的对应点P′的坐标是(C)
A.(-1,6) B.(-9,6) C.(-1,2) D.(-9,2)
7.线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,-2),则点B(-1,-2)的对应点D的坐标为(A)
A.(4,-7) B.(-2,-7) C.(4,-2) D.(-7,4)
8.如图所示:
(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;
(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图形,并写出平移后7个对应点的坐标.
解:(1)A(2,3),B(6,5),C(10,3),D(3,3),E(9,3),F(3,0),G(9,0).
(2)图略.向下平移3个单位长度,即所有点的纵坐标减去3,所以平移后7个对应点的坐标依次为(2,0),(6,2),(10,0),(3,0),(9,0),(3,-3),(9,-3).
9.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是(-5,1).
10.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(D)
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
11.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为(D)
A.(a-2,b+3) B.(a-2,b-3) C.(a+2,b+3) D.(a+2,b-3)
12.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m=-3.
13.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;
(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.
解:(1)三角形ABC向下平移7个单位长度得到三角形A1B1C1.
A1(-3,-3),B1(-4,-6),C1(-1,-5).
(2)三角形ABC向右平移6个单位长度,再向下平移3个单位长度得到三角形A2B2C2.
A2(3,1),B2(2,-2),C2(5,-1).
14.如图,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A′B′C′.
(1)在图中画出三角形A′B′C′;
(2)写出点A′,B′的坐标;
(3)求三角形A′B′C′的面积;
(4)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
解:(1)如图所示.
(2)A′(0,4),B′(-1,1).
(3)S三角形A′B′C′=×4×3=6.
(4)存在.设三角形BCP的边BC上的高为h,
∵三角形ABC的面积和三角形BCP的面积相等,
∴×4×h=6,解得h=3.
∵点P在y轴上,
∴点P的坐标是(0,1)或(0,-5).
15.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为点A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
解:易知AB=6,A′B′=3,
∴a=.
由(-3)×+m=-1,得
m=.
由0×+n=2,得n=2.
设F(x,y),变换后F′(ax+m,ay+n).
∵F与F′重合,
∴ax+m=x,ay+n=y.
∴x+=x,y+2=y.
解得x=1,y=4.
∴点F的坐标为(1,4).
1.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2)
C.(5,2) D.(3,4)
2.将点A(-2,-3)向左平移3个单位长度得到点B,则点B的坐标是( )
A.(1,-3) B.(-2,0)
C.(-5,-3) D.(-2,-6)
3.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是 .
4.平面直角坐标系中,将三角形各点的纵坐标都减去-3,横坐标保持不变,所得图形与原图形相比( )
A.向上平移了3个单位长度
B.向下平移了3个单位长度
C.向右平移了3个单位长度
D.向左平移了3个单位长度
28130505264155.如图,如果将三角形ABC向右平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
A.(5,1)
B.(1,1)
C.(7,1)
D.(3,3)
6.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,点P的对应点P′的坐标是( )
2264410167640A.(-1,6)
B.(-9,6)
C.(-1,2)
D.(-9,2)
7.线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,-2),则点B(-1,-2)的对应点D的坐标为( )
A.(4,-7) B.(-2,-7) C.(4,-2) D.(-7,4)
8.如图所示:
(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;
(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图形,并写出平移后7个对应点的坐标.
9.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是 .
10.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
253873080010011.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a-2,b+3)
B.(a-2,b-3)
C.(a+2,b+3)
D.(a+2,b-3)
12.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m= .
13.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;
(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.
413131083820
14.如图,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A′B′C′.
(1)在图中画出三角形A′B′C′;
(2)写出点A′,B′的坐标;
(3)求三角形A′B′C′的面积;
(4)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
15.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为点A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
参考答案:
7.2.2 用坐标表示平移
1.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是(A)
A.(3,0) B.(1,2)
C.(5,2) D.(3,4)
2.将点A(-2,-3)向左平移3个单位长度得到点B,则点B的坐标是(C)
A.(1,-3) B.(-2,0)
C.(-5,-3) D.(-2,-6)
3.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是(1,1).
4.平面直角坐标系中,将三角形各点的纵坐标都减去-3,横坐标保持不变,所得图形与原图形相比(A)
A.向上平移了3个单位长度
B.向下平移了3个单位长度
C.向右平移了3个单位长度
D.向左平移了3个单位长度
5.如图,如果将三角形ABC向右平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为(A)
A.(5,1) B.(1,1)
C.(7,1) D.(3,3)
6.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,点P的对应点P′的坐标是(C)
A.(-1,6) B.(-9,6) C.(-1,2) D.(-9,2)
7.线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,-2),则点B(-1,-2)的对应点D的坐标为(A)
A.(4,-7) B.(-2,-7) C.(4,-2) D.(-7,4)
8.如图所示:
(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;
(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图形,并写出平移后7个对应点的坐标.
解:(1)A(2,3),B(6,5),C(10,3),D(3,3),E(9,3),F(3,0),G(9,0).
(2)图略.向下平移3个单位长度,即所有点的纵坐标减去3,所以平移后7个对应点的坐标依次为(2,0),(6,2),(10,0),(3,0),(9,0),(3,-3),(9,-3).
9.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是(-5,1).
10.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(D)
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
11.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为(D)
A.(a-2,b+3) B.(a-2,b-3) C.(a+2,b+3) D.(a+2,b-3)
12.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m=-3.
13.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;
(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.
解:(1)三角形ABC向下平移7个单位长度得到三角形A1B1C1.
A1(-3,-3),B1(-4,-6),C1(-1,-5).
(2)三角形ABC向右平移6个单位长度,再向下平移3个单位长度得到三角形A2B2C2.
A2(3,1),B2(2,-2),C2(5,-1).
14.如图,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A′B′C′.
(1)在图中画出三角形A′B′C′;
(2)写出点A′,B′的坐标;
(3)求三角形A′B′C′的面积;
(4)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
解:(1)如图所示.
(2)A′(0,4),B′(-1,1).
(3)S三角形A′B′C′=×4×3=6.
(4)存在.设三角形BCP的边BC上的高为h,
∵三角形ABC的面积和三角形BCP的面积相等,
∴×4×h=6,解得h=3.
∵点P在y轴上,
∴点P的坐标是(0,1)或(0,-5).
15.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为点A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
解:易知AB=6,A′B′=3,
∴a=.
由(-3)×+m=-1,得
m=.
由0×+n=2,得n=2.
设F(x,y),变换后F′(ax+m,ay+n).
∵F与F′重合,
∴ax+m=x,ay+n=y.
∴x+=x,y+2=y.
解得x=1,y=4.
∴点F的坐标为(1,4).
